在谈论线性基之前,先介绍什么是基向量.
根据高中数学,一个二维直角平面坐标系中的所有向量都可以只用(0, 1)和(1, 0)合成.那么(0, 1)和(1, 0)就是基向量,所有基向量能合成的所有向量被称为基向量的张成空间.
在二维空间中,有没有其他的向量能作为基向量呢?答案是肯定的.
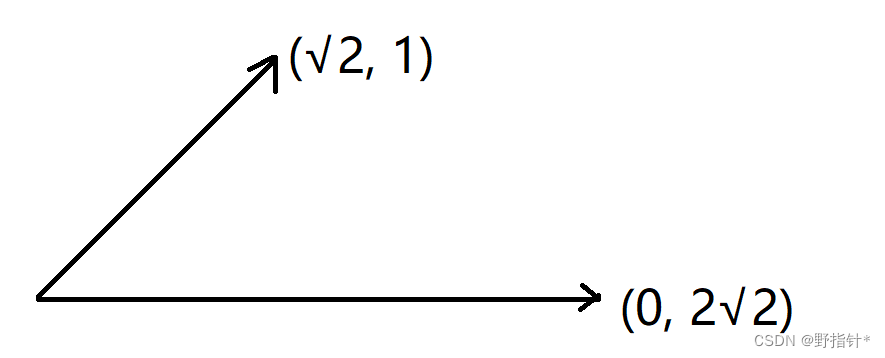
上图的两个向量的张成跟(0, 1)和(1, 0)的张成空间是一样的.
注意到,只要两个向量不共线,其张成都跟(0, 1)和(1, 0)的张成空间一样,即都可以作为二维空间的基向量.
把问题扩展到n维空间,设其基向量为(p1, p2, p3...., pn),如果其中一个向量pi可以由其他的基向量张成,那么这个向量pi一定不是基向量,结论显然,读者可以自证.
这样,一个向量空间的所有基向量被称为这个空间的基.用通俗一点的语言就是,一个空间中任何向量,用这些基向量就能够合成了,而合成这个空间的所有向量至少需要这些基向量.
一个向量空间的基不一定是唯一的.
如果现在我们有一个大小为n的正整数集合,我们想要找出一些数字可以异或出这个集合的所有数字.我们就可以用类似于上面的思路去解决这个问题.把这n个数看成向量,我们要找到一组基能够表示这所有n个数.而这组基就是线性基.
根据上文,我们可以得出一些
线性基的性质:
1.若线性基能够表示一个数x,那么表示这个x的基向量的方案是唯一的,因为如果能找到两组不同的基向量表示出同一个数,其中一组基向量就没有存在的必要.
2.线性基不能表示出0,因为x ^ x = 0,说明线性基中至少存在两组不同的基向量能够同时表示出x,根据1,是不可能的.
线性基的构造:
假设当前的线性基为T,里面已经构造出若干个基向量,分别是T[1], T[2], T[3]....
我们插入某个数x,从最高位开始,如果x的第i位为1,我们尝试用T[i]去分解这个数x,如果T[i]的第i位为0,那么说明x没办法被张成,我们把x作为T[i],完成该次插入;那如果可以分解掉,即T[i]的第i位为1,那么我们就用T[i]分解x,即将x变成x ^ T[i],我们看下一位即可,这样将x一步步分解,最后完成构造.
上面的过程有点抽象,可以看下面的代码,最后构造出来的线性基是大概长这样的:
T[8] = 100100100
T[7] = 010010100
T[6] = 001010110
T[5] = 000110101
T[4] = 000000000
T[3] = 000001010
T[2] = 000000101
T[1] = 000000010
T[0] = 000000001
诶,我们注意到T[4] = 0,刚才不是说线性基不能表示出0吗,怎么T[4] = 0,其实T[4] = 0说明原序列中可能会出现一些数异或起来等于0的情况,但是线性基里面一定不可以出现这种情况,所以T[4] = 0是不算在线性基里面的, 不难推出,如果一个数插入失败了, 说明产生了序列中某些数异或起来等于0.
另外注意到,如果T[i]是线性基,其最高位的1就是第i位.
线性基求max:
根据线性基的构造,我们尝试尽可能大的线性基去合成这个数.所以我们从最高位开始枚举线性基贪心合成即可.
线性基求min:
如果存在异或和为0的情况,直接输出0即可,否则,线性基中最小的基向量就是答案,找到并直接输出即可.
线性基求第k小:
因为线性基张成每个数的方案都是唯一的,所以线性基一共能张成2 ^ t个数(每个数选或者不选),t是线性基的大小.
那么是不是我们直接用二进制分解的方法来选择线性基的数就行了?其实不是,因为根据刚才我们构造的方法,线性基中的数可能不是最小的数(注意上文提到一个向量空间的基可能不是唯一的),为什么不是最小的数就不能表示出第k小呢?那是因为这样选出来的数异或起来可能不是单调递增的.我们怎么在不改变线性基的张成下,让线性基里面的数最小呢?这里有一个贪心的做法,对于T[i],我们尽可能让其低位变成0,于是我们拿T[j](j < i)去消除掉第j位上的1(因为如果T[j]在线性基里面的话,第j位是1),也就是令T[i] = T[i] ^ T[j],最后得到的T肯定都是最小的.因为我们是拿线性基里面的数互相异或,所以不会改变其张成空间.
我们按照以上方法对线性基进行重构以后,就能进行二进制分解了.
线性基合并:
如果当前要合并A,B两个线性基,我们只需要枚举B中的数然后插入A即可,正确性显然,当然反过来做也可以.
补充:
可能会有读者疑惑,在用线性基求min的时候,里面的数可能不是最小值,为什么不用重构线性基,原因是,假如最小的线性基为T[i] = 00001010,其低位可能有1,但是已经没有更小的数可以消除掉低位的1了,所以线性基中的最小数一定就是最小值.
板子:
template<class T>struct Basic{
#define MAXSIZE 62
T f[MAXSIZE + 5], g[MAXSIZE + 5];
int flag, sz;
//flag 记录插入时是否有不能放入的数
void clear() {
memset(f, 0, sizeof f);
flag = sz = 0;
}
void insert(T x){
for (int i = MAXSIZE; i >= 0; --i) {
if (!(x >> i & 1)) continue;
if(!f[i]) {
f[i] = x;
++sz;
return;
}
x ^= f[i];
}
++flag;
}
T queryMax(T res) {
for (int i = MAXSIZE; i >= 0; --i) {
res = max(res ^ f[i], res);
}
return res;
}
T queryMin(){
if (flag) {
return 0;
}
for (int i = 0; i <= MAXSIZE; ++i) {
if (f[i]) {
return f[i];
}
}
return -1;
}
void rebuild(){
for (int i = 0; i <= MAXSIZE; ++i) {
g[i] = f[i];
}
for (int i = 0; i <= MAXSIZE; ++i) {
for (int j = 0; j <= i - 1; ++j) {
if (g[i] >> j & 1) {
g[i] ^= g[j];
}
}
}
}
T queryNum(T k){
//must build g before use it
if (flag) {
--k;
}
if (k == 0) {
return 0;
}
T res = 0;
for (int i = 0; i <= MAXSIZE; ++i) {
if (g[i]) {
if (k & 1) {
res ^= g[i];
}
k >>= 1;
}
}
return k ? -1 : res;
}
Basic merge(Basic A, Basic B) {
for (int i = 0; i <= MAXSIZE; ++i) {
A.insert(B.f[i]);
}
return A;
}
};
Basic<ll> G;