题目

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true，否则返回 false。假设输入的数组的任意两个数字都互不相同。

思路

• 二叉搜索树的特点是：左子树的值 < 根节点 < 右子树的值
• 后序遍历的顺序是：左 → 右 → 中

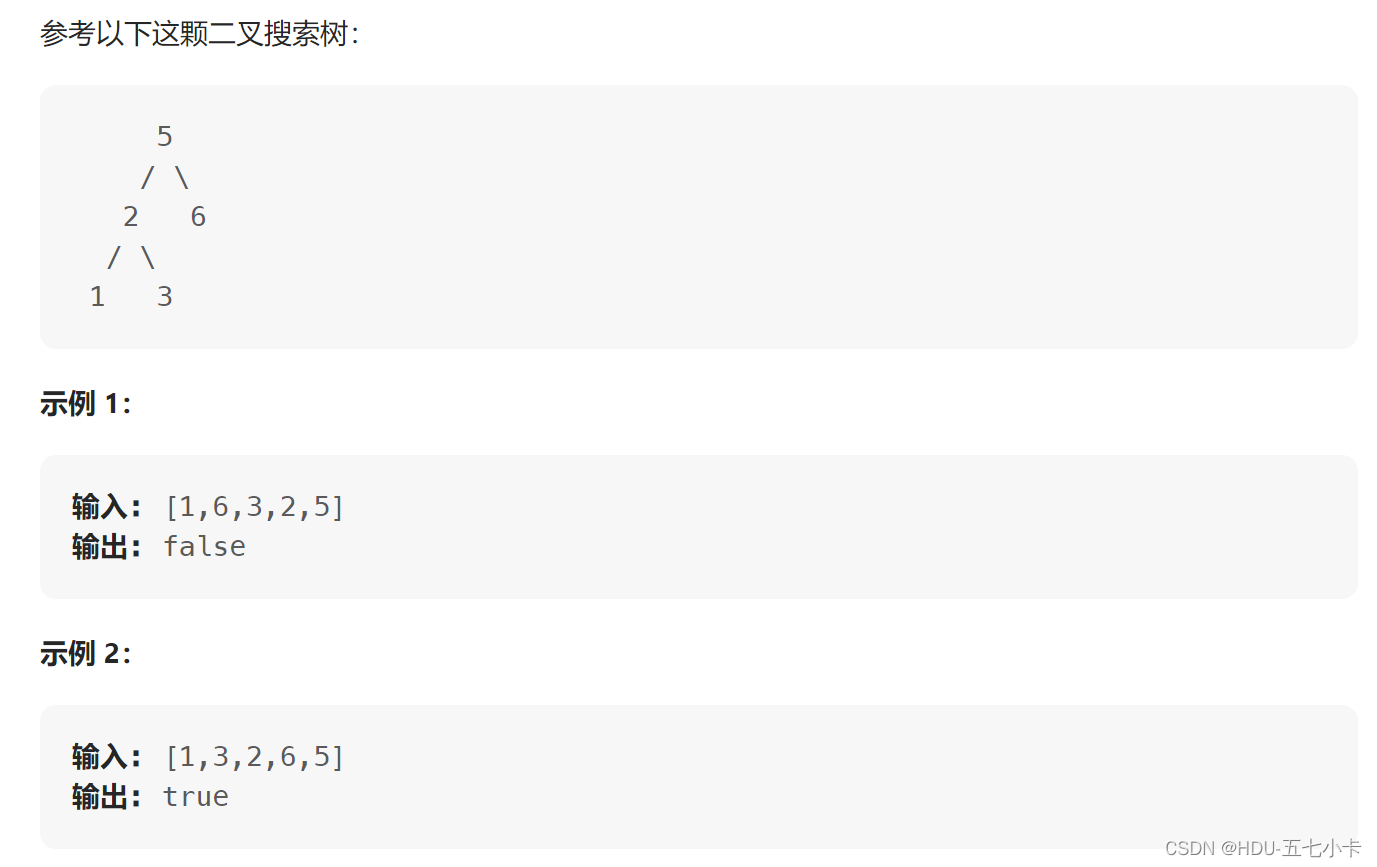
后序遍历中最后一个节点一定是根节点，举个栗子：

下面这棵二叉树，后序遍历结果为：[3，5，4，10，12，9]，则最后一个数字9一定是根节点

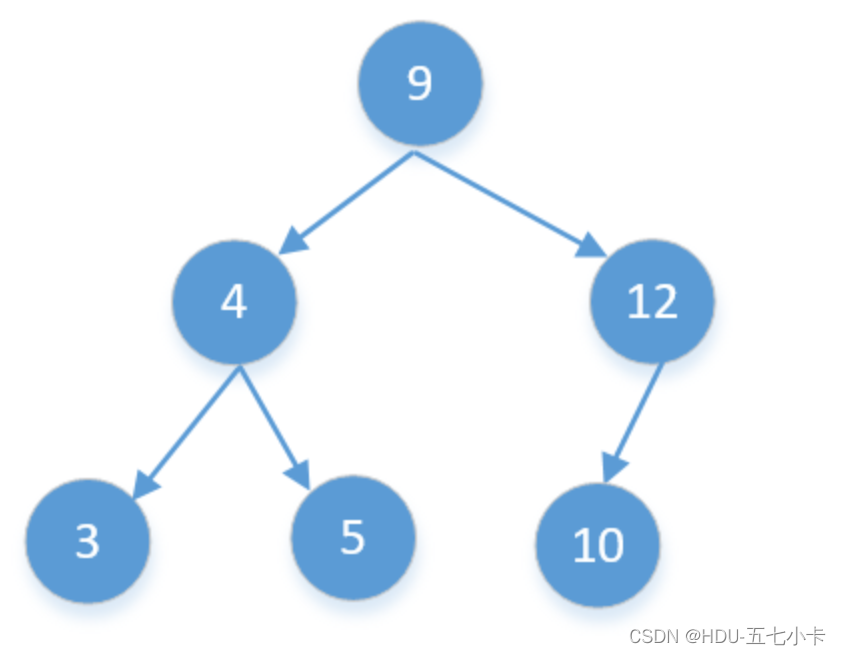
然后在后序遍历结果中从前往后找到第一个比9大的数字10，那么10后面的[10，12]（除了9）都是9的右子节点（因为后序遍历是左右中），10前面的[3，5，4]都是9的左子节点，要注意右子节点后面的需要判断一下，如果有小于9的，说明不是二叉搜索树，直接返回false，最后再以递归的方式判断左右子树。

这里再给出一个反例：下面这棵二叉树不满足搜索树的特点

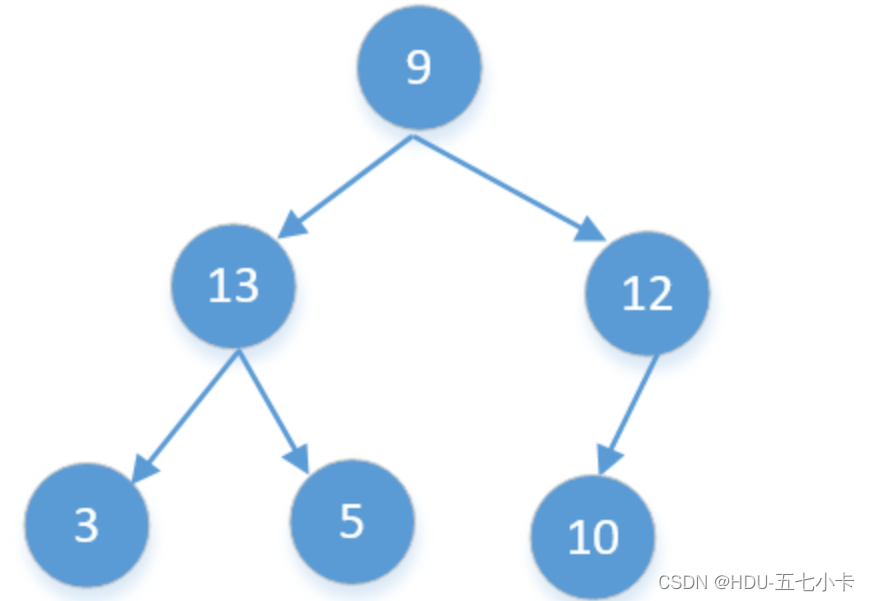
后序遍历为[3，5，13，10，12，9]，接着来根据数组拆分，首先最后一个节点数字9为根节点，第一个比9大的后面都是9的右子节点[13，10，12]。然后再拆分这个数组，12是根节点，第一个比12大的后面都是12的右子节点[13，10]，但可以看到10是比12小的，不可能是12的右子节点，即，确定这棵树不是二叉搜索树。

java代码如下：

class Solution{
	public boolean verifyPostorder(int[] postorder) {
    	return helper(postorder, 0, postorder.length - 1);
}

	boolean helper(int[] postorder, int left, int right) {
	    //如果left==right，就一个节点不需要判断了，如果left>right说明没有节点，
	    //也不用再看了,否则就要继续往下判断
	    if (left >= right)
	        return true;
	    //因为数组中最后一个值postorder[right]是根节点，这里从左往右找出第一个比根节点大的值，他后面的都是根节点的右子节点（包含当前值，不包含最后一个值，因为最后一个是根节点），他前面的都是根节点的左子节点
	    int mid = left;//方便从前往后进行比较判断
	    int root = postorder[right];//根节点
	    while (postorder[mid] < root)//从左往右找到第一个大于根节点的节点
	        mid++;
	    int temp = mid;//复制当前位置到一个副本，方便后面的数字的判断
	    //因为postorder[mid]前面的值都是比根节点root小的，
	    //还需要确定postorder[mid]后面的值都要比根节点root大，
	    //如果后面有比根节点小的直接返回false，因为不满足二叉搜索树的定义
	    while (temp < right) {
	        if (postorder[temp++] < root)
	            return false;
	    }
	    //然后对左右子节点进行递归调用
	    return helper(postorder, left, mid - 1) && helper(postorder, mid, right - 1);
	}
}