🍅 写在前面
👨🎓 博主介绍:大家好,这里是hyk写算法了吗,一枚致力于学习算法和人工智能领域的小菜鸟。
🔎个人主页:主页链接(欢迎各位大佬光临指导)
⭐️近期专栏:机器学习与深度学习
LeetCode算法实例
张量分解
张量分析系列知识,详见下方链接:
张量分解(1)——初探张量
张量分解(2)——张量运算
张量分解(3)——CP分解
张量分解(4)——SVD奇异值分解
张量分解(5)——Tucker分解
本系列文章主要参考论文:Tensor Decompositions and Applications∗
目录
- SVD原理
- SVD形式
- SVD计算
- SVD意义
- SVD分解示例
SVD原理
SVD奇异值分解是一个有着很明显的物理意义的一种方法,它可以将一个比较复杂的矩阵用更小更简单的几个子矩阵的相乘来表示,而可以使用这些小矩阵描述矩阵的重要的特性!和矩阵的特征值特征向量分解有所不同,SVD不需要矩阵为方阵,使用局限性更小。
SVD形式
SVD矩阵分解的形式为:
A
=
U
Σ
V
T
\mathrm{A}=\mathrm{U} \Sigma \mathrm{V}^{\mathrm{T}}
A=UΣVT
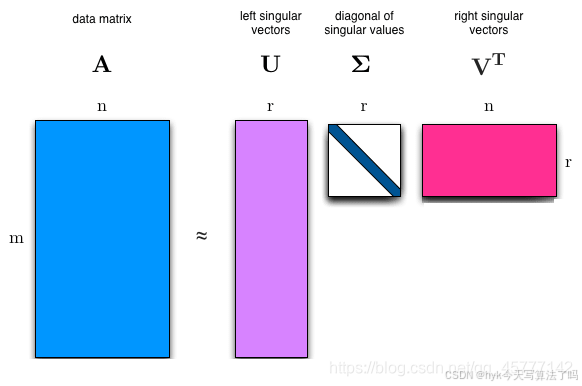
这里假设待分解的矩阵A为m×n维矩阵。U就是m×m维矩阵,名称为左奇异向量。Σ是m×n维矩阵,除了对角线元素,其他元素均是0,对角线元素就是奇异值。V的转置是n×n维的矩阵,名称为右奇异向量。
SVD计算
上面我们给除了SVD分解的形式,那么如何计算公式中的三个参数呢?
1、右奇异向量:
(
A
T
A
)
v
i
=
λ
i
v
i
\left(A^T A\right) v_i=\lambda_i v_i
(ATA)vi=λivi
我们对
(
A
T
A
)
\left(A^T A\right)
(ATA)矩阵求特征值特征向量后,这里的
v
i
vi
vi就是右奇异向量,关于如何求矩阵特征值和特征向量,这里不再详细介绍。
2、奇异值
σ
i
=
λ
i
\begin{aligned} & \sigma_{\mathrm{i}}=\sqrt{\lambda_{\mathrm{i}}} \\ \end{aligned}
σi=λi
对上述特征值开方,即可求得奇异值。
3、左奇异向量
u
i
=
1
σ
i
A
v
i
\begin{aligned} & & \mathrm{u}_{\mathrm{i}}=\frac{1}{\sigma_{\mathrm{i}}} A v_{\mathrm{i}} \end{aligned}
ui=σi1Avi
求得奇异值与右奇异向量,二者按照上方公式计算即可得出左奇异向量。
最后将所求得的各个参数的分量合并在一起,按照形式排列,即可实现奇异值分解。
SVD意义
奇异值与矩阵特征值类似,在Σ矩阵中从大到小排列,但是奇异值减小的非常快,前10%的奇异值之和就占据奇异值总和的99%以上!我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。即: A m × n = U m × m Σ m × n V n × n T ≈ U m × k Σ k × k V k × n T \mathrm{A}_{\mathrm{m} \times \mathrm{n}}=\mathrm{U}_{\mathrm{m} \times \mathrm{m}} \Sigma_{\mathrm{m} \times \mathrm{n}} \mathrm{V}_{\mathrm{n} \times \mathrm{n}}^{\mathrm{T}} \approx \mathrm{U}_{\mathrm{m} \times \mathrm{k}} \Sigma_{\mathrm{k} \times \mathrm{k}} \mathrm{V}_{\mathrm{k} \times \mathrm{n}}^{\mathrm{T}} Am×n=Um×mΣm×nVn×nT≈Um×kΣk×kVk×nT
其中k比n要小很多。简而言之,SVD通过分解数据矩阵,帮助我们在降低数据维度的同时保留最重要的信息,这在数据压缩和去噪中非常有用。在推荐系统中,SVD通过揭示用户和物品的隐含特征,提升了推荐的准确性和个性化水平。
SVD分解示例
- 矩阵 A \boldsymbol{A} A 为: A = ( 0 1 1 1 1 0 ) \mathbf{A}=\left(\begin{array}{ll}0 & 1 \\ 1 & 1 \\ 1 & 0\end{array}\right) A= 011110
- 首先求出
A
T
A
\boldsymbol{A}^T \boldsymbol{A}
ATA 和
A
A
T
\boldsymbol{A} \boldsymbol{A}^T
AAT
A T A = ( 0 1 1 1 1 0 ) ( 0 1 1 1 1 0 ) = ( 2 1 1 2 ) A A T = ( 0 1 1 1 1 0 ) ( 0 1 1 1 1 0 ) = ( 1 1 0 1 2 1 0 1 1 ) \begin{aligned} & \mathbf{A}^{\mathrm{T}} \mathbf{A}=\left(\begin{array}{lll} 0 & 1 & 1 \\ 1 & 1 & 0 \end{array}\right)\left(\begin{array}{ll} 0 & 1 \\ 1 & 1 \\ 1 & 0 \end{array}\right)=\left(\begin{array}{ll} 2 & 1 \\ 1 & 2 \end{array}\right) \\ & \mathbf{A A}^{\mathrm{T}}=\left(\begin{array}{ll} 0 & 1 \\ 1 & 1 \\ 1 & 0 \end{array}\right)\left(\begin{array}{lll} 0 & 1 & 1 \\ 1 & 1 & 0 \end{array}\right)=\left(\begin{array}{lll} 1 & 1 & 0 \\ 1 & 2 & 1 \\ 0 & 1 & 1 \end{array}\right) \\ & \end{aligned} ATA=(011110) 011110 =(2112)AAT= 011110 (011110)= 110121011 - 进而分别求出
A
T
A
\boldsymbol{A}^T \boldsymbol{A}
ATA 和
A
A
T
\boldsymbol{A} \boldsymbol{A}^T
AAT 的特征值和特征向量:
A T A : λ 1 = 3 ; v 1 = ( 1 / 2 1 / 2 ) ; λ 2 = 1 ; v 2 = ( − 1 / 2 1 / 2 ) A A T : λ 1 = 3 ; u 1 = ( 1 / 6 2 / 6 1 / 6 ) ; λ 2 = 1 ; u 2 = ( 1 / 2 0 − 1 / 2 ) ; λ 3 = 0 ; u 3 = ( 1 / 3 − 1 / 3 1 / 3 ) \begin{aligned} & \boldsymbol{A}^{\boldsymbol{T}} \boldsymbol{A}: \lambda_1=3 ; \mathrm{v}_1=\binom{1 / \sqrt{2}}{1 / \sqrt{2}} ; \lambda_2=1 ; \mathrm{v}_2=\binom{-1 / \sqrt{2}}{1 / \sqrt{2}} \\ & \boldsymbol{A} \boldsymbol{A}^T: \lambda_1=3 ; \mathrm{u}_1=\left(\begin{array}{c} 1 / \sqrt{6} \\ 2 / \sqrt{6} \\ 1 / \sqrt{6} \end{array}\right) ; \lambda_2=1 ; \mathrm{u}_2=\left(\begin{array}{c} 1 / \sqrt{2} \\ 0 \\ -1 / \sqrt{2} \end{array}\right) ; \lambda_3=0 ; \mathrm{u}_3= \\ & \left(\begin{array}{c} 1 / \sqrt{3} \\ -1 / \sqrt{3} \\ 1 / \sqrt{3} \end{array}\right) \end{aligned} ATA:λ1=3;v1=(1/21/2);λ2=1;v2=(1/2−1/2)AAT:λ1=3;u1= 1/62/61/6 ;λ2=1;u2= 1/20−1/2 ;λ3=0;u3= 1/3−1/31/3
利用
A
v
i
=
σ
i
u
i
,
i
=
1
,
2
A v_i=\sigma_i u_i, i=1,2
Avi=σiui,i=1,2 求奇异值:
(
0
1
1
1
1
0
)
(
1
/
2
1
/
2
)
=
σ
1
(
1
/
6
2
/
6
1
/
6
)
⇒
σ
1
=
3
(
0
1
1
1
1
0
)
(
−
1
/
2
1
/
2
)
=
σ
2
(
1
/
2
0
−
1
/
2
)
⇒
σ
2
=
1
\begin{aligned} & \left(\begin{array}{ll} 0 & 1 \\ 1 & 1 \\ 1 & 0 \end{array}\right)\binom{1 / \sqrt{2}}{1 / \sqrt{2}}=\sigma_1\left(\begin{array}{l} 1 / \sqrt{6} \\ 2 / \sqrt{6} \\ 1 / \sqrt{6} \end{array}\right) \Rightarrow \sigma_1=\sqrt{3} \\ & \left(\begin{array}{ll} 0 & 1 \\ 1 & 1 \\ 1 & 0 \end{array}\right)\binom{-1 / \sqrt{2}}{1 / \sqrt{2}}=\sigma_2\left(\begin{array}{c} 1 / \sqrt{2} \\ 0 \\ -1 / \sqrt{2} \end{array}\right) \Rightarrow \sigma_2=1 \end{aligned}
011110
(1/21/2)=σ1
1/62/61/6
⇒σ1=3
011110
(1/2−1/2)=σ2
1/20−1/2
⇒σ2=1
也可以用
σ
i
=
λ
i
\sigma_i=\sqrt{\lambda_i}
σi=λi 直接求!
再利用左奇异值求解公式,可得左奇异值。
最终得到A的奇异值分解为:
A
=
U
Σ
V
T
=
(
1
/
6
1
/
2
1
/
3
2
/
6
0
−
1
/
3
1
/
6
−
1
/
2
1
/
3
)
(
3
0
0
1
0
0
)
(
1
/
2
1
/
2
−
1
/
2
1
/
2
)
\mathrm{A}=\mathrm{U} \Sigma \mathrm{V}^{\mathrm{T}}=\left(\begin{array}{ccc} 1 / \sqrt{6} & 1 / \sqrt{2} & 1 / \sqrt{3} \\ 2 / \sqrt{6} & 0 & -1 / \sqrt{3} \\ 1 / \sqrt{6} & -1 / \sqrt{2} & 1 / \sqrt{3} \end{array}\right)\left(\begin{array}{cc} \sqrt{3} & 0 \\ 0 & 1 \\ 0 & 0 \end{array}\right)\left(\begin{array}{cc} 1 / \sqrt{2} & 1 / \sqrt{2} \\ -1 / \sqrt{2} & 1 / \sqrt{2} \end{array}\right)
A=UΣVT=
1/62/61/61/20−1/21/3−1/31/3
300010
(1/2−1/21/21/2)