目录

一、实验要求

二、算法流程

三、案例实现及结果

完整程序：

---

一、实验要求

二、算法流程

粒子群算法流程：

1、初始化：初始化粒子群；给每个粒子赋予初始位置和速度

2、计算适应值：根据适应度函数，计算每个粒子的适应值

3、求个体最佳适应值：对每一个粒子，将其当前位置的适应值与其历史最佳位置对应的适应值比较，如果当前位置的适应值更高，则用当前位置更新历史最佳位置

4、求群体最佳适应值：对每一个粒子，将其当前位置的适应值与其全局最佳位置对应的适应值比较，如果当前位置的适应值更高，则用当前位置更新全局最佳位置

5、更新粒子位置和速度：根据公式更新每个粒子的速度与位置

6、判断算法是否结束：若未满足结束条件，则返回步骤2，若满足结束条件则算法结束，全局最佳位置即全局最优解

三、案例实现及结果

初始化各参数：

学习因子全为c1,c2=1.5；进化参数T=100;种群规模数N=50;粒子堆数D=2;最大速度为1；最小速度为-1；最大粒子为为3，最小粒子位置为-3；对其进行迭代得到如下结果：

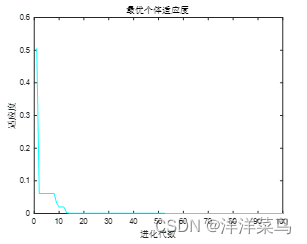
 其中最优个体是：-0.0022800 -0.0000772；最优值为：0.0001353

接下来对上述过程改变单一变量看看结果的变化：

1.改变学习因子的大小，查看适应度值的变化

如图可知，学习因子的变化对结果的影响很小。

2.种群规模大小变化对适应度结果的影响

 

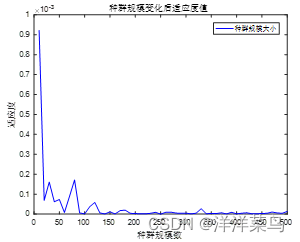
如图可知，种群规模的大小变化的影响，随种群规模的的逐渐增大有了较大的变化，但达到一定程度后便不再变化。

3.速度大小变化对适应度结果的影响

 如图可知，速度变化的影响随着速度的增大逐渐减小，当速度达到0.1以后速度变化的影响几乎为0。

完整程序：

%% 清空环境
clc;
clear all;
close all;

%% 参数初始化
%粒子群算法中的两个参数
c1 = 1.5; %学习因子1
c2 = 1.5; %学习因子2

T=100;   % 进化次数  
N=50;   %种群规模
D=2; %粒子堆数

Vmax=1; %速度最大数
Vmin=-1; %速度最小数
Xmax=3; %位置最大数
Xmin=-3; %位置最小数
[zbest,fitnesszbest]=pso_train(T,N,D,c1,c2,Vmax,Vmin,Xmax,Xmin);
%% 产生初始粒子和速度
X = rand(N,D)*(Xmax-Xmin)-Xmax;
V = rand(N,D)*(Vmax-Vmin)-Vmax;
for i=1:N
    %随机产生一个种群
%     pop(i,:)=rands(1,2)*(Xmax-Xmin)-Xmax;    %初始种群
%     V(i,:)=rands(1,2)*(Vmax-Vmin)-Vmax;  %初始化速度
%     计算适应度
    fit(i)=fun(X(i,:));   %染色体的适应度
end

%% 个体极值和群体极值
[bestfitness bestindex]=min(fit);
zbest=X(bestindex,:);   %全局最佳
gbest=X;    %个体最佳
fitnessgbest=fit;   %个体最佳适应度值
fitnesszbest=bestfitness;   %全局最佳适应度值

%% 迭代寻优
for i=1:T
    for j=1:N
        %速度更新
        V(j,:) = V(j,:) + c1*rand*(gbest(j,:) - X(j,:)) + c2*rand*(zbest - X(j,:));
        V(j,find(V(j,:)>Vmax))=Vmax;
        V(j,find(V(j,:)<Vmin))=Vmin;
        %种群更新
        X(j,:)=X(j,:)+0.5*V(j,:);
        X(j,find(X(j,:)>Xmax))=Xmax;
        X(j,find(X(j,:)<Xmin))=Xmin;
        %适应度值
        fit(j)=fun(X(j,:)); 
    end
    for j=1:N
        
        %个体最优更新
        if fit(j) < fitnessgbest(j)
            gbest(j,:) = X(j,:);
            fitnessgbest(j) = fit(j);
        end
        
        %群体最优更新
        if fit(j) < fitnesszbest
            zbest = X(j,:);
            fitnesszbest = fit(j);
        end
    end 
    yy(i)=fitnesszbest;    
end
%% 结果分析
% 绘图
plot(yy)
title('最优个体适应度','fontsize',12);
xlabel('进化代数','fontsize',12);ylabel('适应度','fontsize',12);
fprintf('最优个体是：%8.7f%8.7f\n',zbest(1),zbest(2))
fprintf('最小值是：%8.7f\n',fun(zbest))