串级计算机控制系统的典型结构如图1所示，系统中有两个PID控制器，Gc2(s)称为副调节器传递函数，包围Gc2(s)的内环称为副回路。Gc1(s)称为主调节器传递函数，包围Gc1(s)的外环称为主回路。主调节器的输出控制量u1作为副回路的给定量R2(s)。
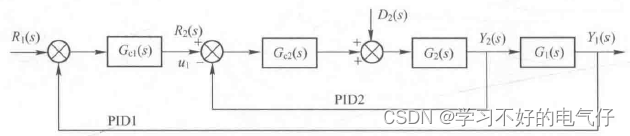
图1 串级控制系统框图
串级控制系统的计算顺序是先主回路（PID1)，后副回路（PID2)。控制方式有两种:一种是异步采样控制，即主回路的采样控制周期T1,是副回路采样控制周期T2,的整数倍。这是因为一般串级控制系统中主控对象的响应速度慢、副控对象的响应速度快的缘故。另一种是同步采样控制，即主、副回路的采样控制周期相同。这时，应根据副回路选择采样周期,因为副回路的受控对象的响应速度较快。
串级控制的主要优点:
(1）将干扰加到副回路中，由副回路控制对其进行抑制;
(2）副回路中参数的变化，由副回路给予控制，对被控量G的影响大为减弱;
(3）副回路的惯性由副回路给予调节，因而提高了整个系统的响应速度。
仿真实例：
设副对象特性为：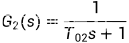
，主对象特性为：
，
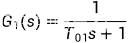,采样时间为2s，外加干扰信号为一幅度为0.01的随机信号d,(k)=0.01rands(1) .
在离散方式下进行仿真，采用M语言进行编程。按预期闭环方法设计副调节器。由于副对象的传递函数为一阶，副回路闭环系统传递函数
。
主调节器采用PI控制，取kp=1.2，ki =0.02。副回路输入、输出及阶跃响应结果如图2~图4所示。
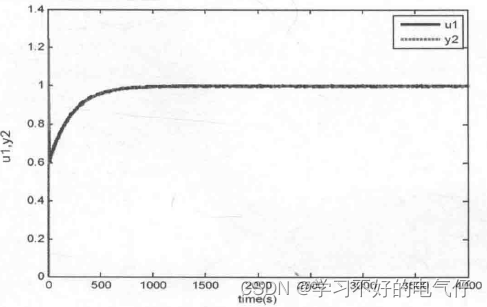
图2 副回路输入、输出
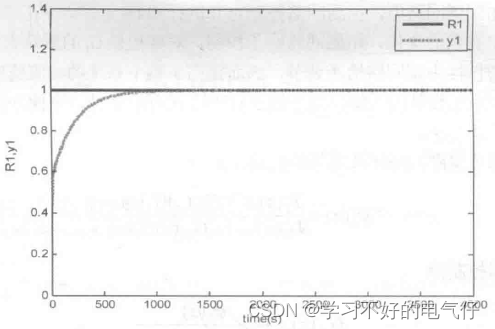
图3 主回路阶跃响应
图4 外加干扰信号
仿真程序：
%Series System Control
clear all;
close all;
ts=2;
sys1=tf(1,[10,1]);
dsysl=c2d(sys1,ts,z');
[num1,den1]=tfdata(dsys1,'v');
sys2=tf(1,[10,1);
dsys2=c2d(sys2,ts,'z);
[num2,den2]=tfdata(dsys2,v');
dph=1/zpk('z',ts);
Gc2=dph/(dsys2*(1-dph));
[nump,denp]=tfdata(Gc2,V);
ul_1=0.0;u2_1=0.0;
yl_1=0;y2_1=0;
e2_1=0;ei=0;
for k=1:1:2000
time(k)k*ts;
R1(k）=1;
%Linear model
y1(k)=-denl(2)*y1_1+num1(2)*y2_1;%Main plant
y2(k)=-den2(2)*y2_1+num2(2)*u2_1;%Assistant plant
error(k)=R1(k)-y1(k);
ei=ei-error(k);
u1(k)=1.2*error(k)H0.02*ei;%Main Controller
e2(k)=u1(k)-y2(k);
%Assistant Controller
u2(k)=-denp(2)*u2_1+nump(1)*e2(k)+nump(2)*e2_1;
d2(k)=0.01*rands(1);
u2(k)=u2(k)+d2(k);
%----------Return of PID parameters-----------------
ul_1u1(k);
u2_1=u2(K);
e2_1=e2(k);
yl_1=y1(k);
y2_1=y2(k);
end
figure(1); %Assistant Controlplot(time,ul,'k",time,y2,'r:',linewidth',2);
xlabel( 'time(s)'):ylabel('u1,y2);
legend('ul','y2');
figure(2);
plot(time,R1,k',time,y1,'re',linewidth’,2);xlabel('time(s));ylabel('R1,y1);
legend('R1','y1');
figure(3);
plot(time,d2,r');
xlabel('time(s)');ylabel('disturbance');
