一、问题

二、分析

1、整体分析

这道题其实就是作者之前讲解过的一道题：AcWing 487. 金明的预算方案（有依赖的背包问题 + 分组背包问题）。这两道题几乎是一模一样的，只不过在之前讲解的那道题目中，所描述的信息形成的树只是一个高度为2的树（不算根节点，因为那道题种的根节点没有意义）。所以我们不需要去存储这个树，只用一个for循环即可。

两道题几乎是一样的，所以这里也是采用分组背包的思路。如果读者不清楚为什么是分组背包的话，建议先去看一看那一篇文章。

下面的解析将围绕着这道题怎么写分组背包展开。

由于这两道题的其中一个不同是树的高度，因此这道题的一个难点是怎么遍历，怎么存储。

我们这里采用邻接表的方式。同时，由于这道题种形成了一棵树，所以我们需要将之前的一层for循环替换成DFS。这两个本质上都是遍历，只不过由于数据结构的不同，我们采取了不同的遍历方式。

这道题还有另外一个难点。

我们之前的那道题种，明确的提到了一个父节点最多只有3个子节点。因此对于这些子节点的选择方案我们可以压缩成一个二进制的数。但是今天这道题不一样了，它的子节点到底有多少并不清楚，如果子节点较多的话，那么我们二进制枚举的时间复杂度将是指数级别的。

所以另外一个难点就是，这道题中的由父节点为代表的组中的物品如何表示？

这里介绍一种新的分类方式：按体积分类

怎么按照体积分类呢?

我们从DP角度重新分析一下本题：

2、状态表示

$f[u][i][j]$，其中$u$代表根节点，$i$表示根节点$u$下面的子树个数，$j$代表的是背包的容量。

那么这个式子表示的就是，在以$u$为根节点的前提下，在$u$的前$i$个子树中选，其中背包容量为$j$的条件下，我们能够携带的最大价值。

3、状态转移

这是个背包问题，根据背包问题的以往的问题来看，我们纠结的是第$i$个物品选不选，那么这里也一样，我们纠结的是第$i$棵子树选不选，如果选的话，怎么选？

那么我们先来解决一下如果选的话，我们怎么选：

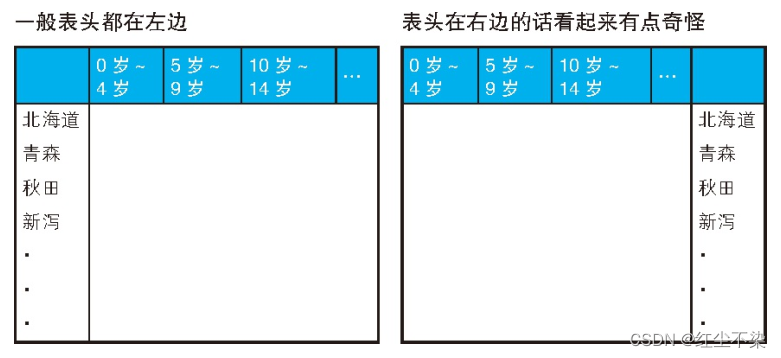
这里我们将子树看成一个组，即物品组，然后按照不同的容量对这些物品进行分类，什么意思呢？

如下图所示：

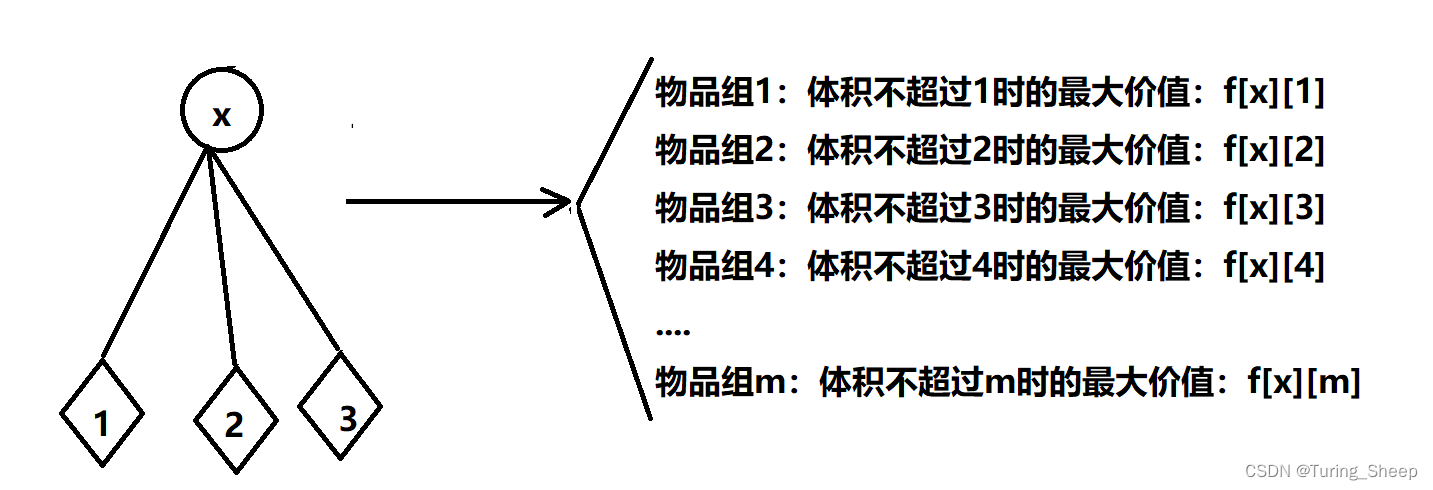
那么怎么选的问题就变成了选几组的问题。

如果不能理解分组背包的思路也没有关系。

我们也可以这么理解。因为$u$的子树我们都可以选，但是分别分配多少的容量是不确定的。因此，我们需要将可能分配的容量都枚举出来，然后再里面选出一个最大值。

如果是后者的理解的话，其实这就是一个01背包问题。

那么转移方程就是：

$$f[u][i][j]=max(f[u][i][j],f[u][i-1][j]+f[x][nums][k])$$

其中：
$k\le j-v[u]$

因为我们选择子树的话，就必须选父节点，所以我们需要把父节点物品的体积空出来。

$x$表示的是第$i$棵子树。

$nums$表示的是子树的子树个数。

4、循环设计

对于组数的枚举需要DFS。

然后枚举容量。

接着写我们的转移方程。

5、初末状态

初始化的话，其实就是$f[u][0][j]$就是说我们不选子树，就要父节点，那么此时选上父节点的物品就是最优选择。因为你不选的话，你价值就是0。

但是我们还要保证放得下父节点代表的物品。

所以$j$要比$v[u]$大。

三、代码

#include<bits/stdc++.h>
using namespace std;
const int N = 110;
vector<int>g[N];
int v[N], w[N];
int n, m;
int f[N][N][N];
void dfs(int u)
{
    
	for(int i = 0; i < g[u].size(); i ++ )
		dfs(g[u][i]);
	
	for(int i = v[u]; i <= m; i ++ )
		f[u][0][i] = w[u];
	
	for(int i = 1; i < g[u].size(); i ++ )
	{
		int son = g[u][i];
		int nums = g[son].size() - 1;
		for(int j = v[u]; j <= m; j ++ )
		{
			for(int k = 0; k <= j - v[u]; k ++ )
			{
				f[u][i][j] = max(f[u][i - 1][j - k] + f[son][nums][k] ,f[u][i][j]);
			}
		}
	}
}
int main()
{
	cin >> n >> m;
	int root = -1;
	for(int i = 1; i <= n; i ++ )g[i].push_back(0);
	for(int i = 1; i <= n; i ++ )
	{
		int a, b, c;
		scanf("%d%d%d", &a, &b, &c);
		if(c == -1)root = i;
		else g[c].push_back(i);
		v[i] = a, w[i] = b;
	}

	dfs(root);
	cout << f[root][g[root].size() - 1][m] << endl;
	return 0;
}

这里可以进行优化，因为我们只用了$i-1$行的数据。因此只需要将容量反过来枚举即可。