看论文的时候有疑惑
R ˙ = R [ ω ] × \dot{\mathbf{R}}=\mathbf{R}[\omega]_{\times} R˙=R[ω]×
R ˙ = [ ω ] × R \dot{\mathbf{R}}=[\omega]_{\times}\mathbf{R} R˙=[ω]×R
难道反对称矩阵乘任意矩阵满足交换性?
在maple里面验证一下吧:
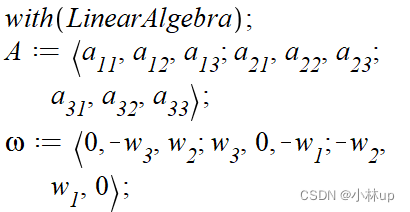
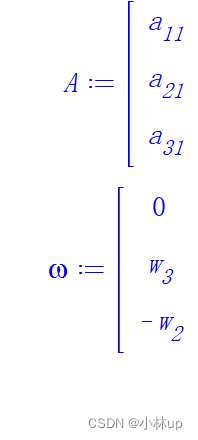
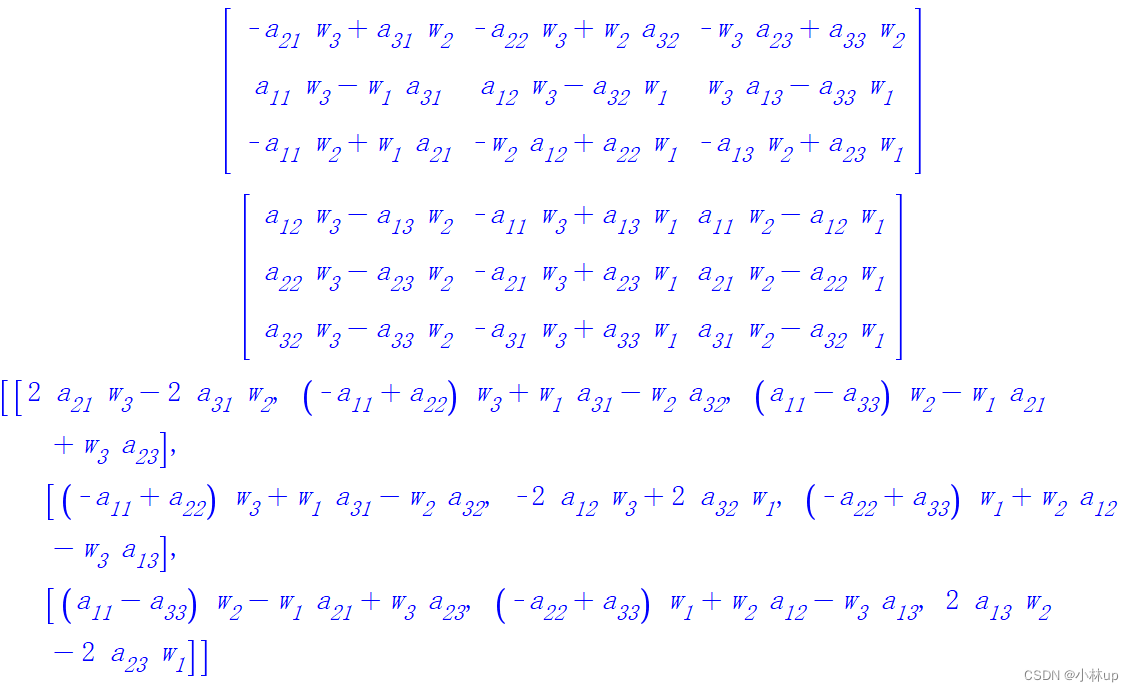
很明显是不一样的,一般的矩阵也不满足交换性质。
至于不同的表示方式表示的是空间角速度和物体角速度罢了,自己记录一下。
看论文的时候有疑惑
R ˙ = R [ ω ] × \dot{\mathbf{R}}=\mathbf{R}[\omega]_{\times} R˙=R[ω]×
R ˙ = [ ω ] × R \dot{\mathbf{R}}=[\omega]_{\times}\mathbf{R} R˙=[ω]×R
难道反对称矩阵乘任意矩阵满足交换性?
在maple里面验证一下吧:
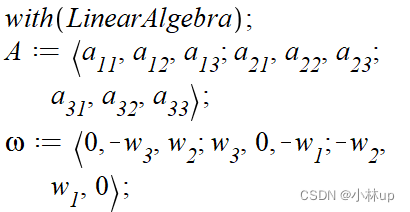
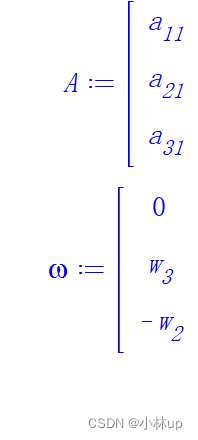
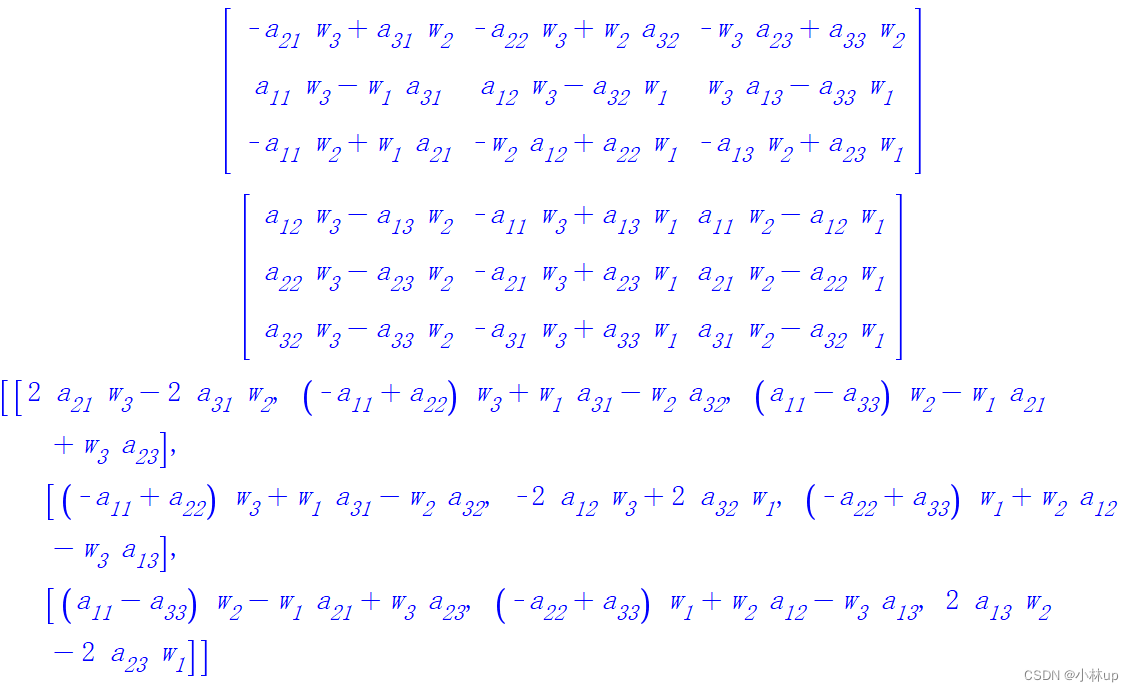
很明显是不一样的,一般的矩阵也不满足交换性质。
至于不同的表示方式表示的是空间角速度和物体角速度罢了,自己记录一下。
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/189202.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!