【数据结构与算法】DP路径问题

news2024/9/20 8:49:39

问题：最小路径和

给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例 1：

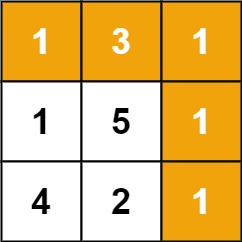
输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

示例 2：

输入：grid = [[1,2,3],[4,5,6]]
输出：12

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j] <= 100

解析与代码

很常规的 DP 问题。设二维数组 dp 记录了从 (0, 0) 出发，到达 (x, y) 的最小路径和。可以在记录 dp 数组时，比较不同路径来源的路径和大小。

class Solution {
    public int minPathSum(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        int[][] dp = new int[m][n];
        dp[0][0] = grid[0][0];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (i == 0 && j == 0) continue;
                int r1 = Integer.MAX_VALUE;
                int r2 = Integer.MAX_VALUE;
                if (i - 1 >= 0) {
                    r1 = dp[i - 1][j] + grid[i][j];
                }
                if (j - 1 >= 0) {
                    r2 = dp[i][j - 1] + grid[i][j];
                }
                dp[i][j] = Math.min(r1, r2);
            }
        }
        return dp[m - 1][n - 1];
    }
}

时间复杂度： $O (n * m)$

空间复杂度： $O (n * m)$

【重点】问题扩展：记录dp路径

如何输出总和最低的路径呢（如果有多个答案，返回其中之一即可）？

这里有个技巧：使用一维数组保存二维信息

如果我们要通过一个一维向量保存一个 $m * n$ 矩阵的坐标，我们可以这样：

int[] g = new int[m * n];

对于任何一个在矩阵中的坐标 (x, y)，我们可以做一个映射：

int getIdx(int x, int y) {
  return x * n + y;
}

同样，可以将一维映射回二维坐标：

int[] parseIdx(int idx) {
  return new int[]{idx / n, idx % n};
}

解决了一维保存二维位置信息问题，下一步是如何记录路径呢？dp 数组的含义是从 (0, 0) 出发，到达 (x, y) 的最小路径和。因此，对于当前坐标 (x, y)，路径矩阵需要记录最小路径和是从哪个方向上更新而来的，在本题中也就是上和左的坐标，哪个小就是从哪里来的。

最后，我们从结尾开始，根据上一步的路径坐标，遍历一次，进行记录保存即可。

class Solution {
    int m, n;
    public int minPathSum(int[][] grid) {        
        m = grid.length;
        n = grid[0].length;
        int[][] f = new int[m][n];
        int[] g = new int[m * n];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (i == 0 && j == 0) {
                    f[i][j] = grid[i][j];
                } else {
                    int top  = i - 1 >= 0 ? f[i - 1][j] + grid[i][j] : Integer.MAX_VALUE;
                    int left = j - 1 >= 0 ? f[i][j - 1] + grid[i][j] : Integer.MAX_VALUE;
                    f[i][j] = Math.min(top, left);
                    g[getIdx(i, j)] = top < left ? getIdx(i - 1, j) : getIdx(i, j - 1);
                }
            }
        }
        
        // 从「结尾」开始，在 g[] 数组中找「上一步」
        int idx = getIdx(m - 1, n - 1);
      
        // 逆序将路径点添加到 path 数组中
        int[][] path = new int[m + n][2];
        path[m + n - 1] = new int[]{m - 1, n - 1};
        for (int i = 1; i < m + n; i++) {
            path[m + n - 1 - i] = parseIdx(g[idx]);
            idx = g[idx];
        }
        // 顺序输出位置
        for (int i = 1; i < m + n; i++) {
            int x = path[i][0], y = path[i][1];
            System.out.print("(" + x + "," + y + ") ");
        }
        System.out.println(" ");
        
        return f[m - 1][n - 1];
    }
  
    int[] parseIdx(int idx) {
        return new int[]{idx / n, idx % n};
    }
  
    int getIdx(int x, int y) {
        return x * n + y;
    }
}