0 结果

较优解：
请添加图片描述
最优解：

1 题目

请添加图片描述

2 思路

为了使 $n_1-n_2｜$ 尽可能小， $S_1-S_2$ 尽可能的大，则需要使划分的两个子集个数尽量想等，较小元素为一个子集，较大元素为一个子集。

2.1 思路1（较优解：排序）

根据前面的思路，对数组进行快速排序得到升序序列，前一个序列取 $\sim n/2-1$ ，后一个序列取 $\sim n- 1$ 。

#include <cstdio>
#include <algorithm>

//快排
void Qsort(int A[], int L, int R){
    if(L >= R) return;
    int pivot, i = L, j = R;
    std::swap(A[L], A[rand()%(R - L + 1) + L]);//快排优化
    pivot = A[L];//比较的基准元素
    while(i < j){
        while(i < j && A[j] > pivot) j--;
        while(i < j && A[i] <= pivot) i++;
        if(i < j) std::swap(A[i], A[j]);
    }
    std::swap(A[L], A[i]);
    Qsort(A, L, i - 1);
    Qsort(A, i + 1, R);
}

void ans(int A[], int n){
    Qsort(A, 0, n - 1);
    //输出S1
    for(int i = 0;i < n/2;i++){
        printf("%d ", A[i]);
    }
    printf("\n");
    //输出S2
    for (int i = n/2; i < n; ++i) {
        printf("%d ", A[i]);
    }
    printf("\n");
}

int main(){
    int A[] = {1, 8,3, 6,5, 4,7,2};
    ans(A, sizeof (A)/sizeof (A[0]));
    return 0;
}

时间复杂度： $O (n l o g n)$
空间复杂度： $O (l o g n)$

2.2 思路2（最优解：类快排思想排序）

对数组 $\sim n-1]$ 进行类似快速排序的做法，在处理左右区间时只处理可能包含中位数的区间，即如果区间的范围是 $[l, r]$ ，则只有 $l <= n /2 - 1 < r$ 才会处理该区间。

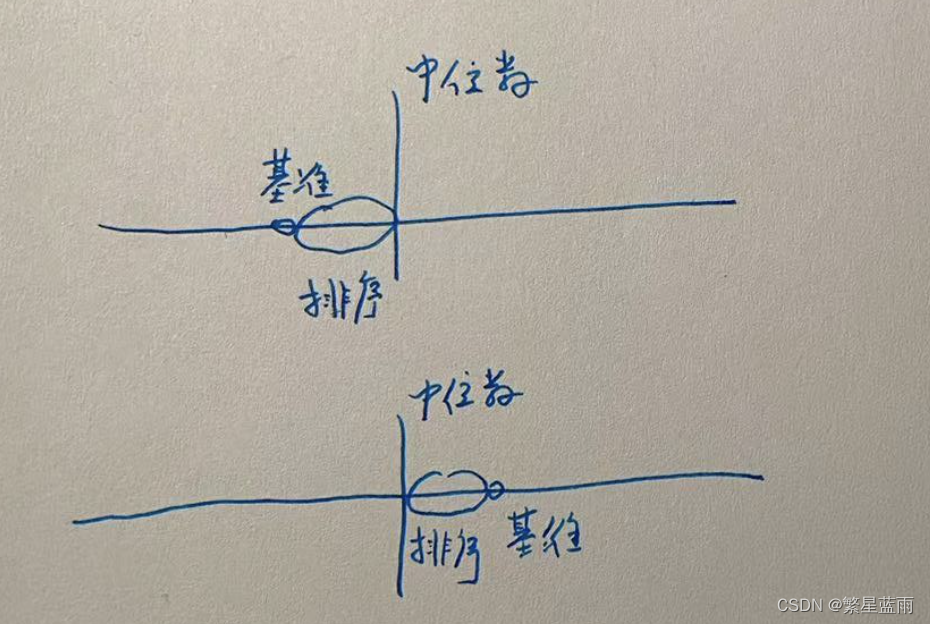
因为快排的基准元素元素左边一定小于等于基准元素，基准元素右边的一定大于等于基准元素，故如果中位数小于基准元素，则只对右边的部分继续排序，中位数大于基准元素，则只对左边的部分继续排序。含义如下图所示：
请添加图片描述

#include <cstdio>
#include <algorithm>

//快排
void Qsort(int A[], int L, int R,int n){
    if(L >= R) return;
    int pivot, i = L, j = R;
    std::swap(A[L], A[rand()%(R - L + 1) + L]);//快排优化
    pivot = A[L];//比较的基准元素
    while(i < j){
        while(i < j && A[j] > pivot) j--;
        while(i < j && A[i] <= pivot) i++;
        if(i < j) std::swap(A[i], A[j]);
    }
    std::swap(A[L], A[i]);
    //以下内容与原快排内容区别
    if(n/2 - 1 >= L && n/2 - 1 <= i - 1)// n/2-1在左区间范围中
        Qsort(A, L, i - 1, n);//递归处理左区间
    if(n/2 - 1 >= i + 1 && n/2 - 1 <= R)
        Qsort(A, i + 1, R, n);
}

void ans(int A[], int n){
    Qsort(A, 0, n - 1, n);
    //输出S1
    for(int i = 0;i < n/2;i++){
        printf("%d ", A[i]);
    }
    printf("\n");
    //输出S2
    for (int i = n/2; i < n; ++i) {
        printf("%d ", A[i]);
    }
    printf("\n");
}

int main(){
    //int A[] = {4, 1, 8,6, 3, 2, 5, 7};
    int A[] = {3,4,2,1,7,8,5,6};//最优解测试序列
    ans(A, sizeof (A)/sizeof (A[0]));
    return 0;
}