目录
1、认识二叉搜索树
2、实现一个二叉搜索树
2.1 成员变量
2.2 insert 方法
2.3 search 方法
2.4 remove 方法(重点)
3、二叉搜索树总结
1、认识二叉搜索树
从字面上来看，它只比二叉树多了搜索两个字，我们回想一下，如果要是在二叉树中查找一个元素的话，需要遍历这棵树，效率很慢，而二叉搜索树，则会效率高很多，为什么呢？
二叉搜索树，可以是一棵空树，或者是具有以下的性质：
- 若它的左子树不为空，则左树上所有的节点都小于根节点
- 若它的右子树不为空，则右树上所有节点的都大于根节点
- 它的左子树和右子树也分别为二叉搜索树
通俗来讲，左孩子都小于父节点，右孩子都大于父节点，以此类推，这里我们画图来认识下二叉搜索树：
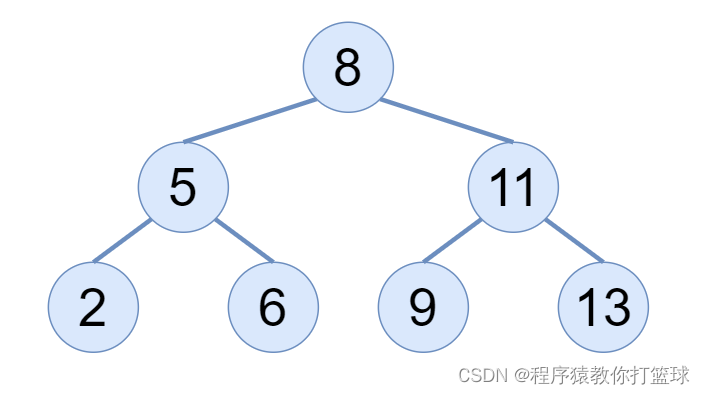
当然二叉搜索树不要求是完全二叉树或满二叉树，甚至会出现单分支的二叉搜索树，所以针对这种特殊的情况进行了优化也就延申而来的 AVL树，这个是后续的话题。
仔细观察上图，可以观察出二叉搜索树的一个新特性：
中序遍历二叉搜索树是有序的，所以二叉搜索树也被称为二叉排序树。
2、实现一个二叉搜索树
2.1 成员变量
public class BinarySearchTree {
private TreeNode root; //存放根节点
private static class TreeNode {
private int val;
private TreeNode left;
private TreeNode right;
private TreeNode(int val) {
this.val = val;
}
}
}这里跟我们的二叉树成员变量大同小异，主要是去实现插入，查找，删除的逻辑。
2.2 insert 方法
往二叉搜索树插入一个节点的时候，我们要注意两点，首先如果二叉搜索树为空，则直接令 root 为当前插入的节点即可，那如果二叉搜索树不为空，我们则需要利用二叉搜索树的性质，找到该节点要插入的位置即可，具体我们来看下图：
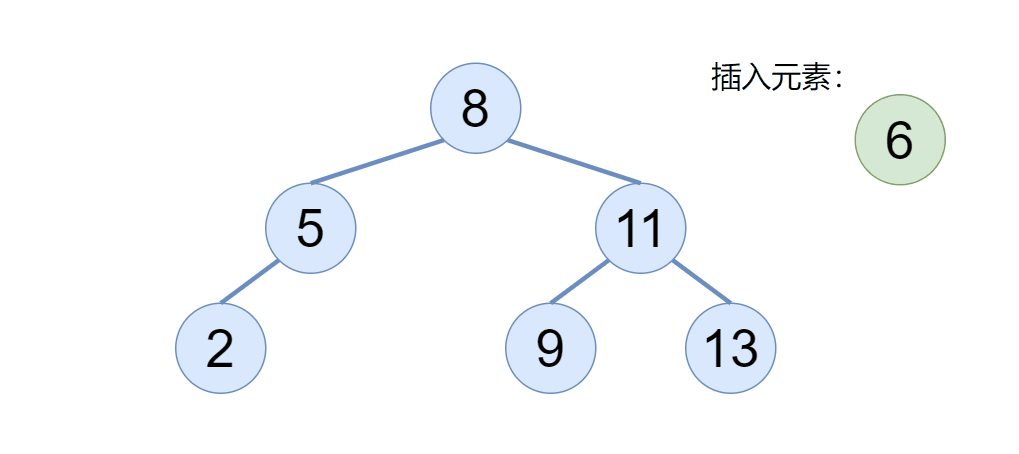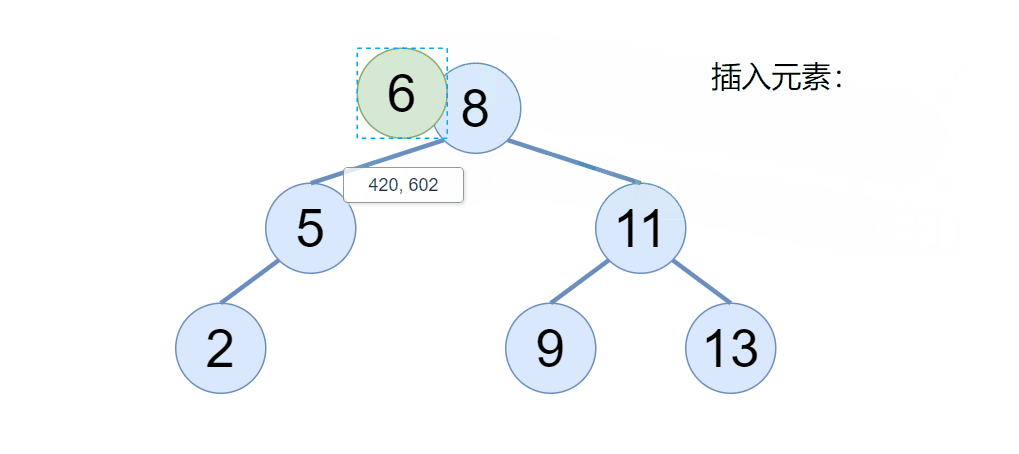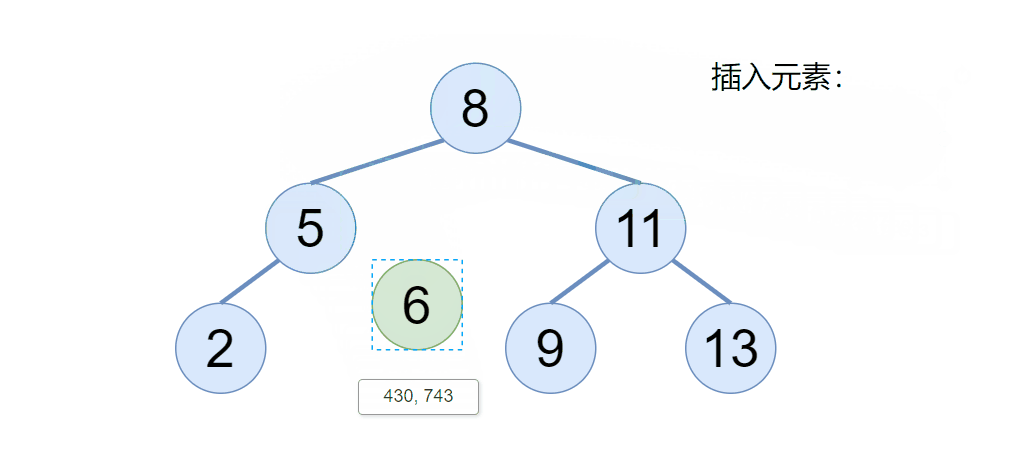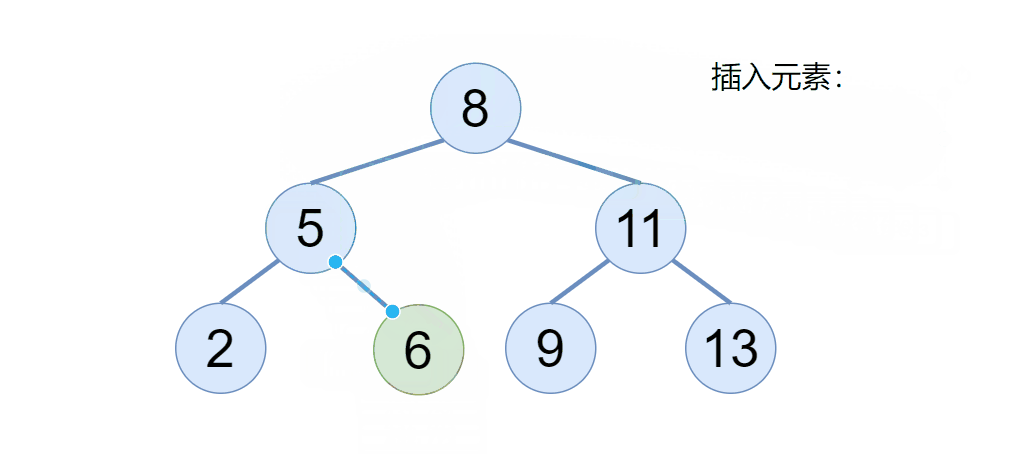
通过动图我们可以看到，当二叉搜索树不为空的时候，新的元素会依次节点比较，如果比根节点大，则去根的右边，比根节点小，则取根的左边，以此类推。(搜索二叉树不存在相同的元素)
但是我们用代码如何实现呢？定义一个 cur 引用，当 cur 等于 null 了，则表示是我要插入的位置，既然找到了要插入的位置，但是还得知道这个位置的父节点是谁，通过父节点的指针域给连接起来，于是代码可以这样写：
public boolean insert(int key) {
// 二叉搜索树没有节点的情况
if (root == null) {
root = new TreeNode(key);
return true;
}
// 二叉搜索树不为空的情况 -> 找到该节点要插入的位置进行插入
// 如果已经存在该节点了, 则不用插入 -> 二叉搜索树中不能出现重复值
TreeNode parent = null; // 记录cur的父节点
TreeNode cur = root;
while (cur != null) {
if (cur.val < key) {
parent = cur;
cur = cur.right;
} else if (cur.val > key) {
parent = cur;
cur = cur.left;
} else {
return false; // 插入重复的节点
}
}
// 走到这, cur为空了, key 需要插入到 parent 的左节点或右节点中
TreeNode newNode = new TreeNode(key);
if (parent.val < key) {
parent.right = newNode;
} else {
parent.left = newNode;
}
return true;
}2.3 search 方法
搜索方法，也就是给一个 key 你，让你在这颗二叉树找有没有这个元素，有的话返回该节点，没有的话返回 null，这个就很简单了， 跟上面的步骤一样无非就是碰到相同的元素返回 cur 嘛，当 cur 根据 key 遍历完这棵二叉搜索树的时候，也就是 cur 为 null 了，则表示没有该元素，直接返回 null即可。
代码如下：
public TreeNode search(int key) {
TreeNode cur = root;
while (cur != null) {
if (cur.val < key) {
cur = cur.right;
} else if (cur.val > key) {
cur = cur.left;
} else {
return cur;
}
}
return null;
}2.4 remove 方法(重点)
在二叉搜索树中，删除一个节点是一个比较麻烦的事，但是只要把各种删除的情况下列举出来，一一解决它即可，对于二叉搜索树来说，你删除了一个节点，它仍然满足二叉搜索树的性质。
设 cur 为要删除的节点，所以首先我们得判断这个二叉搜索树中，是否存在要删除的节点，这个逻辑上面已经写过了，找到要删除的节点后，我们一共会面临三种情况：
① 如果 cur 没有左子树的情况
- 如果 cur 是 root 的情况，只需要 root = cur.right
- 如果 cur 不是 root，cur 是 parent.left 的情况，只需要 parent.left = cur.right
- 如果 cur 不是 root，cur 是 parent.right 的情况，只需要 parent.right = cur.right
图解：
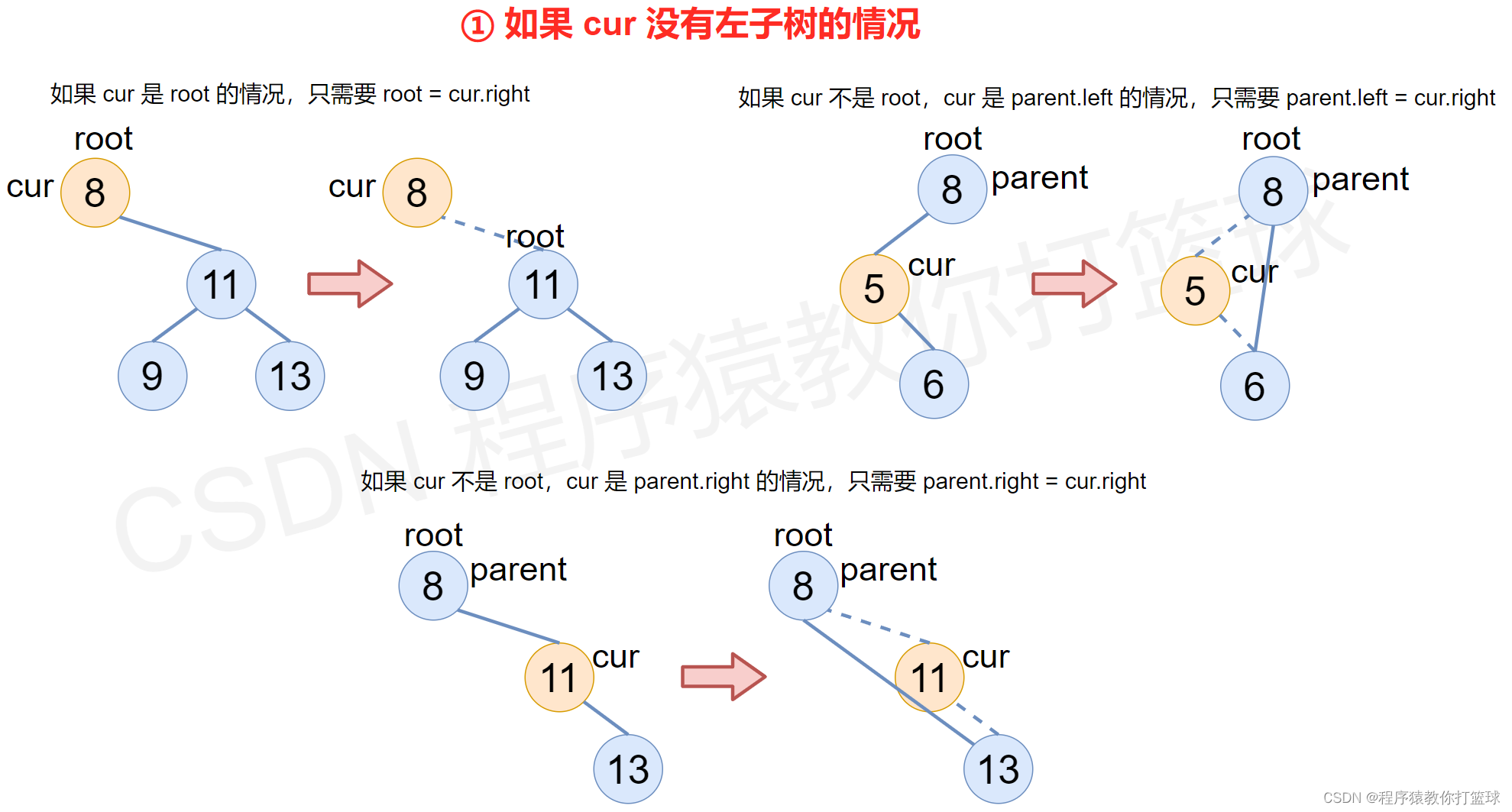② 如果 cur 没有右子树的情况
- 如果 cur 是 root 的情况，只需要 root = cur.left
- 如果 cur 不是 root，cur 是 parent.left 的情况，只需要 parent.left = cur.left
- 如果 cur 不是 root，cur 是 parent.right 的情况，只需要 parent.right = cur.left
图解：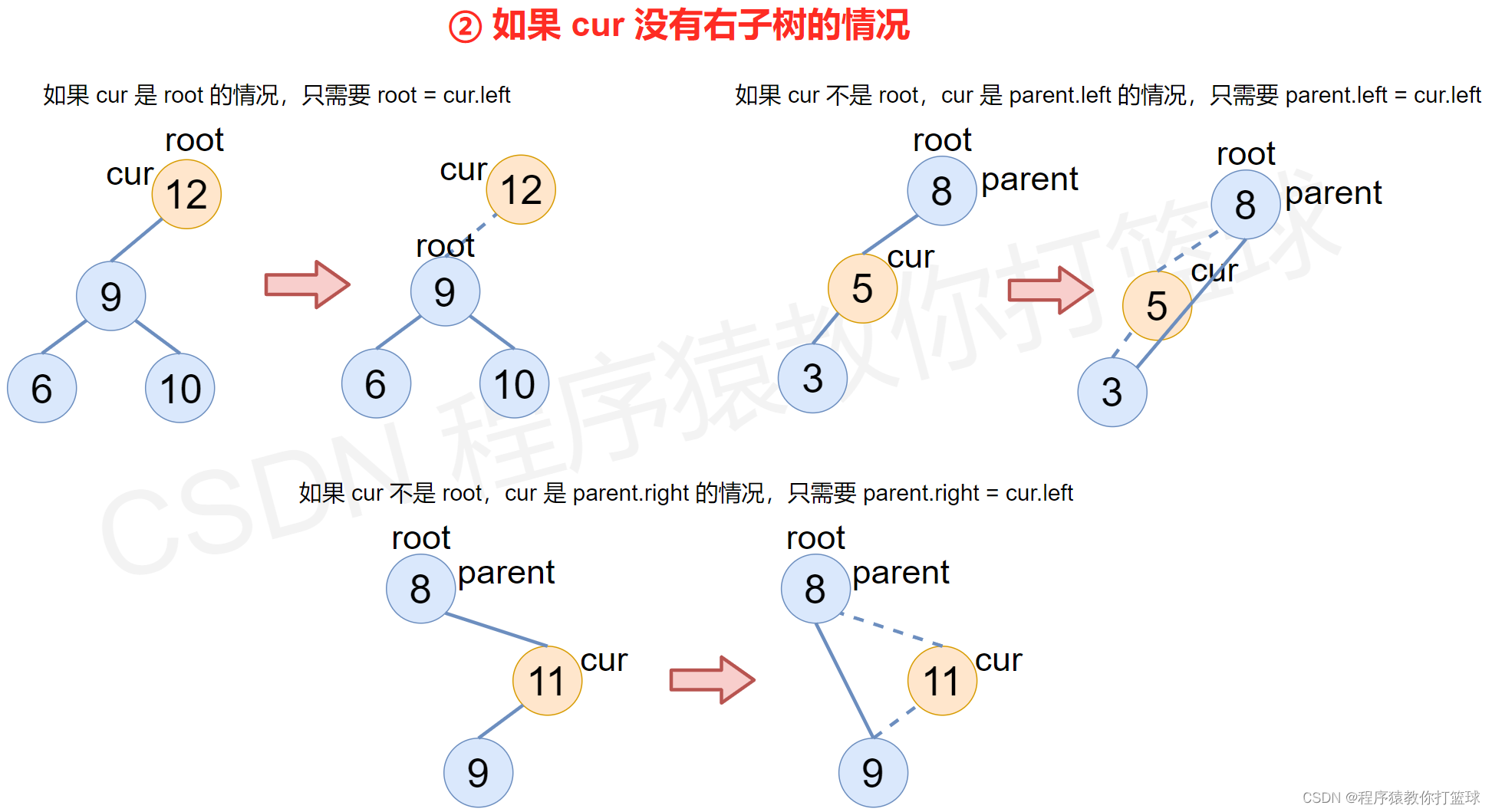 
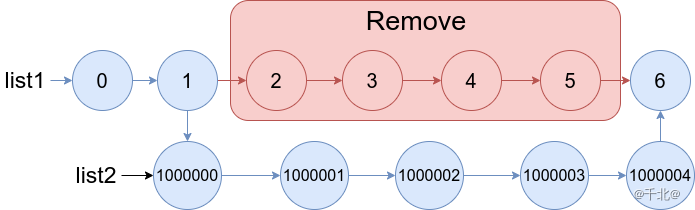
③ 如果 cur 既有左子树，又有右子树的情况
- 使用替换法进行删除，即在 cur 的右子树中，一直往左寻找最小的元素，将这个最小值赋值给要删除节点的 val 值中，接着把这个最小元素的节点删除即可，删除的逻辑见下图和完整删除代码。
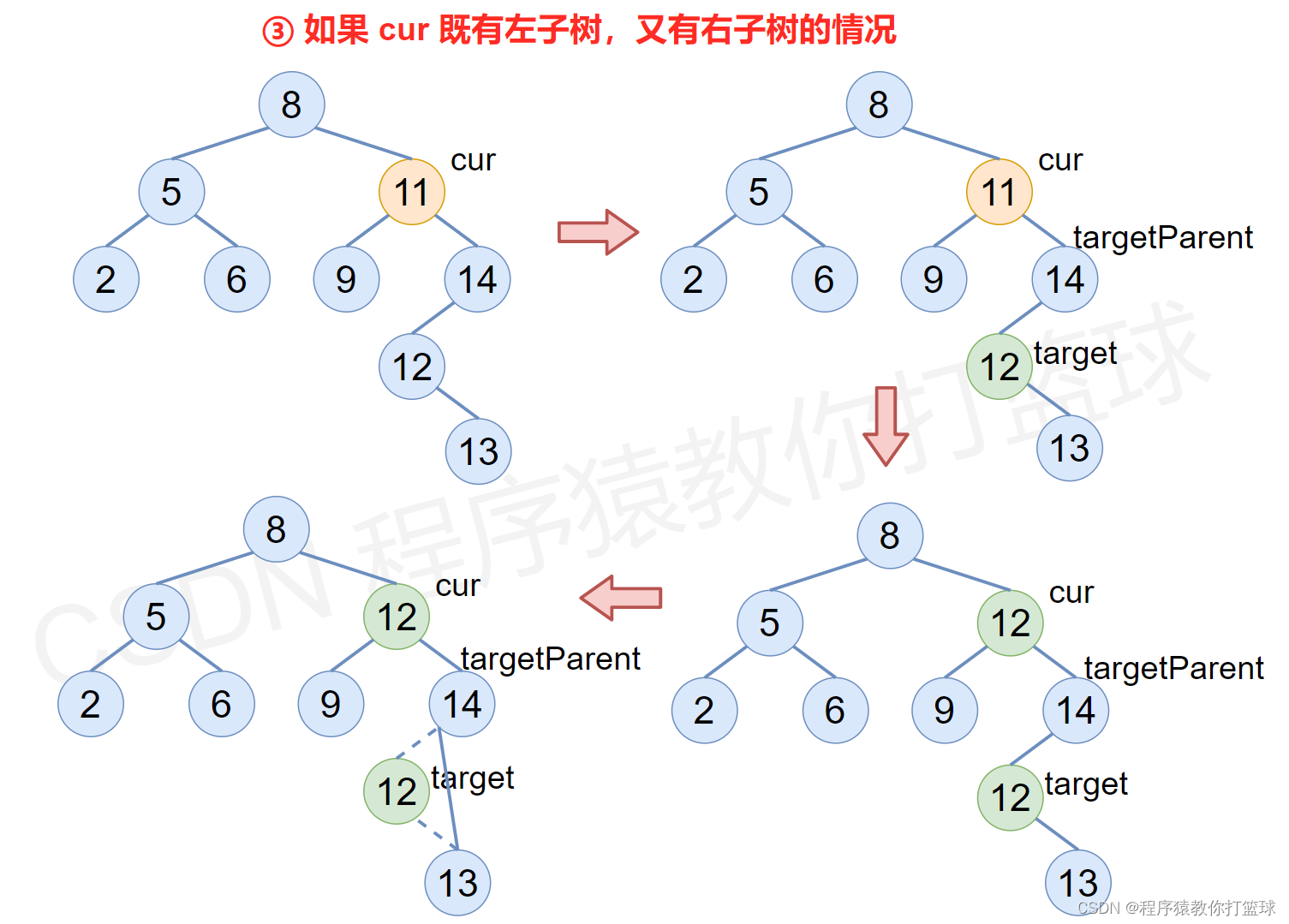
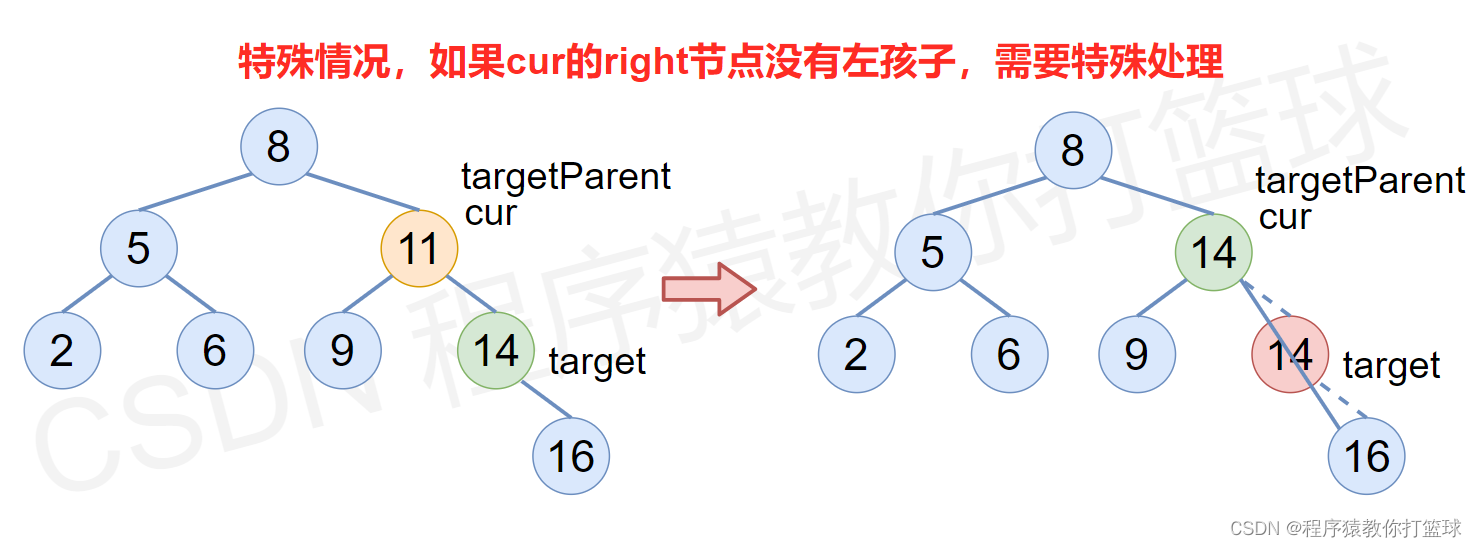
代码如下：
public boolean remove(int key) {
TreeNode parent = null;
TreeNode cur = root;
while (cur != null) {
if (cur.val < key) {
parent = cur;
cur = cur.right;
} else if (cur.val > key) {
parent = cur;
cur = cur.left;
} else {
removeNode(parent, cur);
return true;
}
}
return false;
}
private void removeNode(TreeNode parent, TreeNode cur) {
if (cur.left == null) {
if (cur == root) {
root = cur.right;
} else if (cur == parent.left) {
parent.left = cur.right;
} else {
parent.right = cur.right;
}
} else if (cur.right == null) {
if (cur == root) {
root = cur.left;
} else if (cur == parent.left) {
parent.left = cur.left;
} else {
parent.right = cur.left;
}
} else {
TreeNode target = cur.right;
TreeNode targetParent = cur;
while (target.left != null) {
targetParent = target;
target = target.left;
}
// 走到这, target就是要删除节点的右子树中最小的节点, 接下来进行覆盖
cur.val = target.val;
// 覆盖完成, 现在需要删除 target 节点
// 如果 cur.right 没有左孩子的情况, 此时的target就是cur.right
// 即直接将 cur.right 覆盖到 cur 位置, 也就是满足 target == targetParent.right 条件
// 所以需要进行特殊处理.
if (target == targetParent.right) {
targetParent.right = target.right;
} else {
targetParent.left = target.right;
}
}
}3、二叉搜索树总结
二叉搜索树在最好的情况下为完全二叉树，查找的平均比较次数为：logn
二叉搜索树在最差的情况下退化成但分支，查找的平均比较次数为：n/2
所以二叉搜索树在最差的情况下效率是不高的，为了解决单分支的情况，于是有了 AVL树，当发现二叉搜索树左右子树高度差太大，会自动旋转，以致平衡，避免旋转的次数太多，又引入了红黑树，给节点增加了颜色，细节部分后期讲解，这里有个概念即可，下期将会介绍由红黑树作为底层的集合：TreeSet 和 TreeMap
下期预告： 【Java 数据结构】TreeSet 和 TreeMap
