题目
思路
建议先看看详解rmq问题
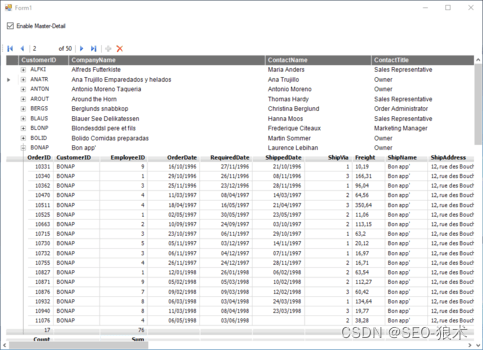
很明显这道题意是跟你一段数列,并给出多次询问,询问区间内最大值和最小值的差。
如果去暴力枚举显然会超时,所以要用st算法来解决。
我们要建立两个RMQ预处理内容,分别处理最大值和最小值。
建一个mx[i][j]代表从i开始,长度为2^j的区间内的最大值,mn[i][j]代表从i开始,长度为2^j的区间内的最小值。
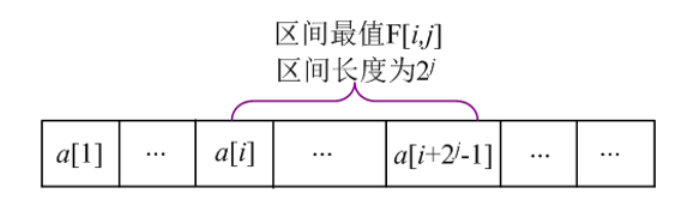
根据倍增思想,长度为2^j的区间可被分成两个长度为2^(j-1)的子区间,然后求两个子区间的最值即可。所以在预处理时将该区间从中间平均分成两部分(中间有重叠没关系,不影响求最值),每一部分的元素个数恰好为2^j-1个,也就是说,状态转移方程为:
mx[j][i] = max(mx[j][i - 1],mx[j + s[i - 1]][i - 1])
mn[j][i] = min(mn[j][i - 1],mn[j + s[i - 1]][i - 1])
(s[i]代表2^i次方)
若F[i, j]表示[i, i+2^j-1]区间的最值,区间长度为2^j,则i和j的取值范围是多少呢?
若数组的长度为n,最大区间长度2^r≤n<2^(r+1),则r=⌊log2n⌋,比如n=8时k=3,n=10时k=3。在程序中,r=log2(n),i从1~i<=r,j从1~s[i]+j-1<=n(因为i代表区间长度,j代表区间的开始位置)
预处理代码:
void pre()
{
int r = log2(n);
for(int i = 1; i <= r; i++)
for(int j = 1; s[i] + j - 1 <= n; j++)
{
mx[j][i] = max(mx[j][i - 1],mx[j + s[i - 1]][i - 1]);
mn[j][i] = min(mn[j][i - 1],mn[j + s[i - 1]][i - 1]);
}
}预处理完后,就要开始查询了。
若查询[l,r]区间的最大和最小值,则首先计算k值,和前面的计算方法相同,区间长度为r-l+1,
2^k≤r-l+1<2^(k+1),因此k=log2(r-l+1) 。
若查询区间的长度大于或等于2^k且小于2^(k+1),则根据倍增思想,可以将查询区间分为两个查询区间,取两个区间的最值即可。两个区间分别为从l向后的2^k个数及从r向前的2^k个数,这两个区间可能有重叠,但对求最值没有影响。
查询代码:
int f(int x,int y)
{
int r = log2(y - x + 1);
int t1 = max(mx[x][r],mx[y - s[r] + 1][r]);
int t2 = min(mn[x][r],mn[y - s[r] + 1][r]);
return t1 - t2;
}整体代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
int t,n,q,a[1000001],mx[1000001][20],mn[1000001][20],s[1000001],x,y;
void pre()
{
int r = log2(n);
for(int i = 1; i <= r; i++)
for(int j = 1; s[i] + j - 1 <= n; j++)
{
mx[j][i] = max(mx[j][i - 1],mx[j + s[i - 1]][i - 1]);
mn[j][i] = min(mn[j][i - 1],mn[j + s[i - 1]][i - 1]);
}
}
int f(int x,int y)
{
int r = log2(y - x + 1);
int t1 = max(mx[x][r],mx[y - s[r] + 1][r]);//最大
int t2 = min(mn[x][r],mn[y - s[r] + 1][r]);//最小
return t1 - t2;//差
}
signed main()
{
s[0] = 1;
for(int i = 1; i <= 20; i++) s[i] = s[i - 1] * 2;//s[i]代表2^i次方
scanf("%lld%lld",&n,&q);
for(int i = 1; i <= n; i++)
{
scanf("%lld",&t);
mx[i][0] = mn[i][0] = t;//初始化,从第i个位置向后延2^0位的最大值和最小值都是输入的第i个位置上的数
}
pre();//预处理
for(int i = 1; i <= q; i++)
{
scanf("%lld%lld",&x,&y);
printf("%lld\n",f(x,y));//查询
}
return 0;
}