作为一种数据结构，哈希桶有着不同于其他数据结构的思想——直接映射，这使得在哈希结构中查找数据的效率达到了最快的O(1)，比起搜索树的比较数据大小，选择左右子树中的一颗进行遍历的查找算法，在需要进行大量查找的场景中，哈希明显是我们的最佳选择。而针对一些特殊场景，虽然没有使用哈希的桶结构，但是哈希的思想却体现的淋漓尽致，为深入学习哈希，我们来看这几个常见的应用场景

位图应用

question 1

1.给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在这40亿个数中

第一种思路：将所有的数存储到set中，使用set进行数据的查找。这个时候我们就要意识到关联式容器的缺点：需要额外的空间维护结构，搜索树需要保存parent和左右子树的根节点，哈希桶需要维护指针数组与一个单链表，节点需要维护next指针，这些都是额外的开销，很有可能无法维护40亿的数据。

第二种思路：外排序后进行二分查找，首先在磁盘上进行排序的效率极低，其次二分查找需要容器支持随机访问，文件能支持随机访问吗？其实是可以的，但不像数组一样可以直接访问数据，文件只支持顺序访问，所谓随机访问只是使文件指针不断遍历数据，随机停下，到达一个随机的效果。但是移动文件指针同样很慢，外排序的思路也是不行

最后一个思路：直接映射数据的出现次数到数组中。首先我们需要存储的结果是：是否出现过，所以对于一个数据只有两种状态，出现过和没有出现过，用1表示数据出现过，用0表示数据没有出现过，用数组的下标表示数据的值，对应下标的位置上保存0或1。判断一个无符号整数是否出现过，只要将其作为数组的下标获取该位置上的数据是否为1即可。但这就有一个问题，如果这40亿个数据中包含了无符号整数的最大值和最小值，那么用来保存出现结果的数组会非常的大（因为数组的下标将达到最大的无符号整数值）假设数组的每个元素都是char，大小1字节，那这个数组将占用4个G的内存，开销非常大。但是存储0或1需要使用1字节的char类型吗？显然1个bit就能存储0或1这两种情况，所以我们可以用1个char存储8个数据的存在结果，只需要对char数据进行位运算
用最小的单位bit存储数据是否出现过的结果，将内存的开销缩小到原来的1/8，极大的节约了内存。C++也提供了相应的容器：bitset，注意它的模板参数，类型是size_t，我们要传入一个无符号整数N作为bitset的长度，当然了，位图的成员只占用了一个bit，假设N为16，bitset中的数组大小为16/8，2个字节

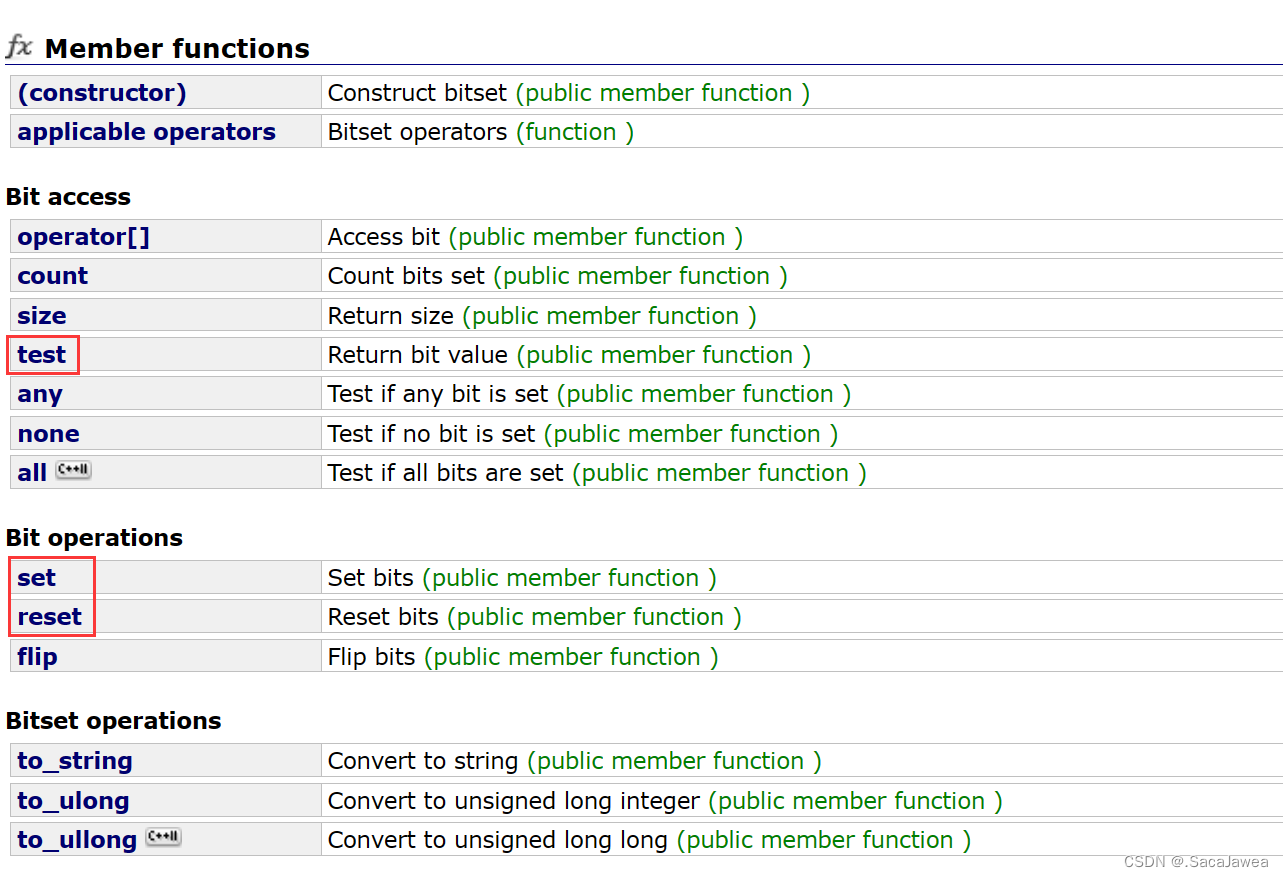
对于位图结构，最经常的接口有三个

test：检查pos位置的数据是否存在，返回bool值
set：将pos位置标记为存在，表示数据存在
reset：将pos位置标记为不存在，表示数据不存在

一开始位图数据的标记都是不存在。总结一下这个问题：给定海量的无符号数据，判断某个数据是否存在？这个问题的关键在于是否存在是一个二元结果，用0或1就能表示，所以我们就能用极少的空间存储数据是否出现的标记位，就算数据的跨度很大，内存也能hold住（如果有无符号long，还是有可能hold不住的）。判断是否存在时，只需要用给定的整数作为数组的下标访问该bit位的数据的标记即可。

question 2

给定100亿个整数，设计算法找到只出现一次的整数？

注意这里不再是判断是否存在这样的二元问题，而是只出现一次，对出现次数进行枚举：用0表示数据可能没有出现，用1表示数据出现1次，用2表示数据出现两次及以上，需要保存的存在情况从二元到了三元，一个bit显然无法存储三种情况，所以这里可以用过两个bit位存储这三种情况。即使用两张位图，一张位图表示两个bit位的高位，一张表示bit位的低位，00表示数据没有出现过，01表示数据出现一次，10或者11表示数据出现二次及以上。因此我们还是可以使用bitset容器，只是要封装一下，将一个容器当作高位，一个当作低位。最后还要注意的是：题干中说给定的是整数，即有可能是负数，所以这里的映射需要间接一下，将给定的数据加上最小整数的绝对值后才是数据映射的下标，即最小的整数映射数组的位置为0，0映射的位置是最小整数的绝对值

总结一下，这题是位图的变形，虽然变了但变了不多

question 3

给两个文件，分别有100亿个整数，我们只有1G内存，如何找到两个文件交集？

给定100亿个整数，假设整数的类型是int，100亿个int大概是40G的大小，这些整数肯定不能保存到容器中，除非电脑的内存多于80G。注意题目让我们求交集，也就是说需要保存数据是否出现过，保存一个二元结果，自然的想到了位图，int数据的范围在2的负31次方到2的31次方-1之间，两者之差大概在2的32次方，所以需要长度为2的32次方的位图，2的32次方bit大概是500M。不过我们需要明白，位图可没有保存数据啊，位图只是用数组的下标间接的表示数据的大小（或者说，用数组元素的地址与首元素的地址之间的差值表示数据的值），位图存储的只是0和1。

我们先打开A文件，读取其中的数据，创建一个位图记录数据是否出现，接着打开B文件，读取其中的数据，也创建一个位图记录数据是否出现，然后将A位图作为最后保存交集的结构，从0开始遍历整个A位图，如果在A文件出现的数据也在B文件出现，A位图不变，如果数据只在A文件出现，将该数据在A位图的映射标记为0，最后A位图就是两个文件数据的交集。总结一下，创建两个位图记录两个文件的数据是否出现，接着对两个位图做“与”运算，将结果保存到其中一个位图中，该位图就是两个文件的交集

位图的作用

讲到这里，我们总结一下位图的作用

1.位图有去重的作用，对一个位置多次调用set()接口，只是将该位置标记为1
2.位图自带排序功能，只要从0开始遍历位图，一次打印保存1的位置的下标，得到的就是升序排序的数据

哈希切分

给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址？
与上题条件相同，如何找到top K的IP？

可以注意到，位图的直接映射是建立在需要保存的结果种类较少的情况下，比如是否出现，出现次数不超过2，一个是二元结果，一个是四元结果，对于四元结果，我们可以使用两张位图，对于八元结果我们用三张位图…但是题目问的是出现次数最多的数据呢？出现次数最多会达到多少？我们不得而知，只有遍历完所有数据，我们才能知道，此时我们可以使用多张位图来表示数据的出现次数吗？首先最多的出现次数是一个未知数，我们无法预测，既然无法知道数据的具体范围，我们就不能提前创建位图，所以这里我们不能使用多种位图来表示数据的出现次数。回到题目，我们需要将IP和其出现次数作为键值对，存储在map中，极端一点，假设几乎所有P地址都不相同，只有一串IP地址出现两次，我们就需要将这100G的IP地址和其出现次数保存到map中，然后遍历map达到出现次数最多的IP。显然内存是不够的，较少的内存只支持我们一次统计一部分IP地址，所以我们需要将大文件分成多份小文件，当统计下一个小文件时，保存上次统计结果的map就需要被释放（因为内存不足），如果一个IP还没有统计完，就释放保存其出现结果的map，这样统计得到的结果将是错误的。所以我们需要一次性将相同IP的出现次数统计完，后续的统计不能出现这一IP，也就是说大文件分成的小文件需要包含同样IP的所有副本，这里有两个限制，一个是小文件不能过大，因为需要将小文件加载到内存中。二是相同IP的副本都要被放到这个小文件中，这个条件优先级高于第一个条件，所以在切分小文件时，我们要先保证一个IP的所有副本被移动到一个小文件中，然后再保证该文件的大小是否过大，如果过大该文件不能再存储其他IP，只能存储IP的副本

现在的问题就是：如果得到一个IP的所有副本？答案是设计一个哈希函数，将IP地址这个字符串转换成整数，整数就是文件的编号，A1,A2,A3…A100，所以我们只需要遍历一遍大文件，将所有IP映射成整数，再将这些IP存储到整数对应的文件中。通常的小文件不会过大，但是有一种可能，就是大文件中有的IP地址出现次数很多，极端一点，100G的文件80G都是这个IP的副本，此时切分得到的小文件中，肯定有一个小文件大小超过80G，但是统计这个小文件时，没有创建其他键值对，只是对一个IP的键值对中的出现次数不断++。我们说100G的IP地址无法加载到内存中，是假设几乎所有的IP地址都出现了一次，此时我们就要为每个IP创建一个键值对并保存其出现次数，键值对的创建将用光所有内存，但是100G的IP地址全是一个IP的副本呢？此时只要创建一个键值对，然后只需要修改键值对中的IP出现次数，这个操作又不会再使用内存，所以看似100G的数据，结果map的去重后可能只有1，2G。但是这只是两个极端情况，我们需要考虑的全面一些，如果一个小文件又全是几乎不相同的IP地址呢？程序统计该文件时，肯定会因为要创建键值对而申请内存失败，所以我们需要捕获申请内存失败的异常，在处理方法中再次用不同的哈希函数对小文件做切分。

至此，从大文件到小文件的哈希切分就没有大问题了，需要额外注意的操作就是：捕获申请内存失败的异常，用新的哈希函数重新切分小文件，再进行统计操作。每统计完一个小文件，遍历保存IP及其出现次数的map表，将出现次数最多的IP以及出现次数用一个键值对另外保存下来，接着用这个map表统计下一个小文件，遍历得到该文件中出现次数最多的IP，与之前保存的IP出现次数比较，谁多保留谁。当统计完所有的小文件，另外保存的键值对就是出现次数最多的IP及其出现次数

至于另一个变形问题：如何找出出现次数top K的IP？只需要将另外保存的键值对换成一个小堆，然后就是典型的top K问题了

布隆过滤器

如果将question 1变形

给定100G的文件，快速判断一个IP地址是否在该文件中

与第一个问题不同，需要判断的不再是整数，而是一个字符串，又和哈希切分不同，哈希切分是用来统计出现次数的，而且不能说它快速，那么判断IP是否存在可以用位图吗？虽然IP不是一个整数，但是将其转换成指定范围内的一个整数也是可以的，对于判断IP是否出现就转换成了一个整数是否出现。但是将字符串转换成整数会又问题吗？我们知道整数有限，int，long都有最大的值，表示的数量就那么多，但是字符串是无限的，将无限的数据转换成有限的数据，可能存在与其他数据冲突的情况吗？答案是这样的情况很经常发生，比如"192.168.1.1"和"127.0.0.1" 这两个字符串都转换成了66这个整数，当文件只有"127.0.0.1"这个IP时，我判断"192.168.1.1"是否存在于文件中，由于两IP转换后的整数一样，所以得到的结果是"192.168.1.1"存在于文件中，但实际并不存在。

针对上面的问题：无限的数据类型转换成有限的数据类型会发生冲突，我们的解决思路是用更多有限的数据表示无限的数据，降低冲突发生的概率。这就是布隆过滤器的思想，将位图的直接映射和多种哈希转换结合。刚刚的例子，"192.168.1.1"被三个哈希函数转换后得到用66，55，44这三个数，"127.0.0.1"可以被三个哈希函数转换后得到66，77，88这三个数，在"127.0.0.1"存在的情况下，"192.168.1.1"还会存在吗？虽然两个IP的三个整数有一个冲突了，但是最后的结果是两者不再冲突。因为只有66，77，88这三个位置都为1，才表示"192.168.1.1"存在，现在只有66的位置为1，"192.168.1.1"不与"127.0.0.1"发生冲突，即此时没有发生误判。

话虽如此，无限转有限的情况下，误判还是会发生的，布隆过滤器只是降低了冲突发生的概率，并且布隆过滤器不存储数据本身，不像位图的直接映射，数组下标就表示了数据本身，布隆过滤器只存储了数据转换后的映射结果，是一种间接映射，并且较难逆向得到原先数据，因为存在着哈希冲突以及转换顺序的不确定。所以，布隆过滤器的特点是

1.当查询结果为存在时，可能发生误判，这是无法避免的
2.当查询结果为不存在时，不存在误判，该数据就是不存在
3.不能删除数据，因为哈希映射的整数可能部分冲突，一个数据删除可能会影响到其他数据，如果支持了删除，连数据不存在都会发生误判
4.如果用引用计数来支持数据的删除，布隆过滤器将会占用大量内存，因为引用计数的上限无法确定，不仅占用内存大还难以进行维护

对于布隆过滤器的使用，我们需要创建一些哈希转换函数，还需要设置用来保存数据映射结果的数组长度，要怎么设置才能使哈希冲突的概率降到最低，并且占用最少的内存，这里可以参考这篇博客，最后再总结一下布隆过滤器的优缺点

优点
1.查找效率高，时间复杂度为O(K)，K是哈希函数的个数
2.由于哈希函数之间是异步的，所以可以并行调用哈希函数（勉强算个优点吧）
3.不存储数据本身，保密性好，并且较难逆向得到原数据
缺点
1.有误判，且无法避免，只有数据不存在才是一定准确的
2.不能获取元素本身且无法删除元素