前言

众所周知，链表可以用结构体和指针来实现，而栈和队列可以直接调用STL，那为什么还要费尽心思用数组来实现这三种数据结构呢？

首先，对于用结构体和指针实现的链表，每次创建节点都要使用 new 关键字，这一步非常慢，尤其是当链表的长度 $\geq10^5$ 时，用这种方法构造的链表在处理各种操作时很有可能TLE。其次，STL容器本身就要比原生数组慢，当数据量非常庞大的时候，使用数组来模拟这些数据结构是一个不错的选择。

一、用数组实现链表

1.1 单链表

通常，我们习惯用结构体和指针来实现单链表（两个成员变量+三个构造函数）：

struct ListNode {
    int val;
    ListNode *next;
    ListNode() : val(0), next(nullptr) {}
    ListNode(int x) : val(x), next(nullptr) {}
    ListNode(int x, ListNode *next) : val(x), next(next) {}
};

我们把用上述方式实现的链表称为动态链表，把用数组方式实现的链表称为静态链表。具体来说

使用动态链表存储数据，无需预先申请内存空间，而是在需要的时候用 malloc 或 new 关键字进行申请，所以链表的长度没有限制。动态链表因为是动态申请内存的，所以每个节点的物理地址不连续，需要通过指针来顺序访问；
使用静态链表存储数据，需要预先申请足够大的一块内存空间，所以链表的初始长度一般是固定的。静态链表因为是用数组实现的，所以每个节点的物理地址连续。

对于动态链表，每个节点不仅存储了一个值，还存储了指向下一个节点的指针，在动态链表上进行移动也是用的指针。静态链表自然也需要具备这些特性，那如何用数组的方式进行实现呢？

不妨给链表中的节点从 $0$ 开始编号，如果链表有 $n$ 个节点，则编号依次为 $0,1,\cdots,n-1$ 。每个节点的编号可以视为指向该节点的「指针」，于是用指针访问节点便成了用「索引」访问节点（因为索引就是从 $0$ 开始的）。设链表可能达到的最大长度为 $N$ ，因此开两个数组分别用来存储每个节点的值和指向下一个节点的指针：

int val[N], nxt[N];  // val用来存储每个节点的值，nxt用来存储指向下一个节点的指针

例如，对于下图中的链表（红色为节点编号，黑色为节点存储的值）

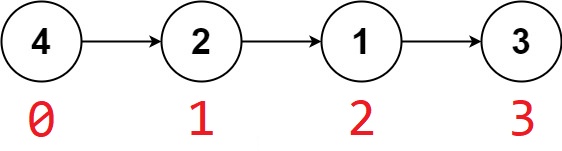
val 数组和 nxt 数组应当分别为（规定空指针为 $- 1$ ）

val[0] = 4, nxt[0] = 1;
val[1] = 2, nxt[1] = 2;
val[2] = 1, nxt[2] = 3;
val[3] = 3, nxt[3] = -1;

当然，仅用这两个数组来表示链表是远远不够的，我们还需要头指针 head 和一个指向待插入位置的指针 idx（因为是从小到大进行编号的，所以 idx 只会增加不会减少）

int head, idx;  // head是头指针，idx是指向待插入位置的指针，只增不减

头指针始终指向链表的头节点。初始时，链表为空，头指针为空指针，因此有 head = -1。因为链表中没有节点，故位置 $0$ 待插入，所以 idx = 0。链表的初始化函数如下

void init() {
    head = -1, idx = 0;
}

接下来，我们研究静态链表的插入与删除操作。

操作一：在链表头部插入元素 x。

因为 idx 为待插入的位置，因此执行 val[idx] = x 相当于创建了一个节点，接下来执行 nxt[idx] = head 相当于让该节点指向头节点，最后执行 head = idx 让头指针指向该节点。当然，不要忘了 idx++，因为 idx 已经被用过了（已经被编号了），因此待插入的位置变成 idx + 1。

void insert(int x) {
    val[idx] = x, nxt[idx] = head, head = idx++;
}

操作二：在第 $k$ 个插入的数后面插入一个数 x。

⚠️ 第 $k$ 个插入的数并不是指当前链表的第 $k$ 个数。例如操作过程中一共插入了 $n$ 个数，则按照插入的时间顺序，这 $n$ 个数依次为：第 $1$ 个插入的数，第 $2$ 个插入的数， $\cdots$ ，第 $n$ 个插入的数。

显然，idx 记录了插入顺序。即 idx 所指向的节点为按照时间顺序第 idx + 1 个插入的数（注意 idx 是从 $0$ 开始的）。

void insert(int k, int x) {
    val[idx] = x, nxt[idx] = nxt[k - 1], nxt[k - 1] = idx++;
}

操作三：删除第 $k$ 个插入的数后面的数， $k = 0$ 时表示删除头节点。

void remove(int k) {
    if (k) nxt[k - 1] = nxt[nxt[k - 1]];
    else head = nxt[head];
}

⚠️ 切勿写成 nxt[k - 1] = nxt[k]，因为编号只在数组中连续，但不一定在链表中连续，所以 nxt[k - 1] 不一定等于 k。

操作四：输出链表。

for (int i = head; ~i; i = nxt[i]) cout << val[i] << ' ';

📝 ~i 等价于 i != -1。

我们可以用面向对象的思维对上述代码进行封装，使其更加清晰易懂：

class List {
private:
    int val[N], nxt[N], head, idx;

public:
    List() : head(-1), idx(0) {}

    void insert(int x) {
        val[idx] = x, nxt[idx] = head, head = idx++;
    }

    void insert(int k, int x) {
        val[idx] = x, nxt[idx] = nxt[k - 1], nxt[k - 1] = idx++;
    }

    void remove(int k) {
        if (k) nxt[k - 1] = nxt[nxt[k - 1]];
        else head = nxt[head];
    }

    void display() {
        for (int i = head; ~i; i = nxt[i]) cout << val[i] << ' ';
    }
};

一个使用范例：

#include <iostream>

using namespace std;

const int N = 1e5 + 10;

class List {...};  // 这里省略

int main() {
    List *ll = new List();
    ll->insert(3);
    ll->insert(4);
    ll->insert(5);
    ll->insert(6);
    ll->remove(4);  // 第4个插入的数是6，所以该操作将会删除6后面的5
    ll->display();  // 输出：6 4 3
    delete ll;
    return 0;
}

1.2 双链表

用结构体和指针实现的双链表如下（三个成员变量+三个构造函数）：

struct ListNode {
    int val;
    ListNode *prev;
    ListNode *next;
    ListNode() : val(0), prev(nullptr), next(nullptr) {}
    ListNode(int x) : val(x), prev(nullptr), next(nullptr) {}
    ListNode(int x, ListNode *prev, ListNode *next) : val(x), prev(prev), next(next) {}
};

如何用数组来实现双链表呢？

回顾单链表的实现方式，我们定义了两个数组，一个用来存储节点的值，一个用来存储指向下一个节点的指针。类比到双链表，我们需要三个数组，如下

int val[N], pre[N], nxt[N];
// val用来存储节点的值
// pre用来存储指向上一个节点的指针
// nxt用来存储指向下一个节点的指针

同样地，我们还需要一个指针 idx 用来指向待插入的位置。注意到单链表是单向的，因此只需要一个头指针 head，而双链表是双向的，所以不仅需要头指针 head，还需要尾指针 tail。

为简便起见，我们省略掉头指针和尾指针，定义 $0$ 号节点和 $1$ 号节点，这两个节点实际上是两个边界，链表的实质内容在这两个节点之间更新。链表的头节点是 nxt[0]，链表的尾节点是 pre[1]，整个链表（加上两个边界）形如

$\rightleftarrows\textcolor{red}{ \text{nxt[0]}\rightleftarrows \text{nxt[nxt[0]]}\rightleftarrows \cdots\rightleftarrows \text{pre[pre[1]]}\rightleftarrows \text{pre[1]} }\rightleftarrows \text{1}$

红色部分才是链表的实质内容， $0$ 和 $1$ 仅仅起到边界的作用。

初始时，链表为空，且形如 $0\rightleftarrows1$ 。因为 $0$ 和 $1$ 已经被用过了，所以 idx 应当从 $2$ 开始。链表的初始化函数如下

void init() {
    nxt[0] = 1, pre[1] = 0, idx = 2;
}

接下来，我们研究双链表的插入与删除操作。

操作一：在第 $k$ 个插入的数后面插入一个数 x。

我们先来看如何在编号为 $k$ 的数后面插入一个数。

首先执行 val[idx] = x 来创建一个节点。然后执行 pre[idx] = k, nxt[idx] = nxt[k] 来建立新节点与已有节点之间的单向链接，最后执行 pre[nxt[k]] = idx, nxt[k] = idx 来建立双向链接（注意这里的顺序不能写反），当然不要忘了 idx++。

void insert(int k, int x) {
    val[idx] = x, pre[idx] = k, nxt[idx] = nxt[k];
    pre[nxt[k]] = idx, nxt[k] = idx++;
}

而实际上，第 $k$ 个插入的数的编号为 $k + 1$ （因为 idx 是从 $2$ 开始的，例如第 $1$ 个插入的数的编号就是 $2$ ），因此实现操作一需要这样调用

insert(k + 1, x);

操作二：在第 $k$ 个插入的数前面插入一个数 x。

注意到第 $k$ 个插入的数的编号为 $k + 1$ ，因此该操作相当于在 pre[k + 1] 的后面插入一个数 x，故可以直接调用操作一中的函数

insert(pre[k + 1], x);

操作三：在链表的头部插入数 x。

该操作等价于在 $0$ 的后面插入 x，直接调用即可

insert(0, x);

操作四：在链表的尾部插入数 x。

该操作等价于在 $1$ 的前面插入 x，也等价于在 pre[1] 的后面插入 x，直接调用即可

insert(pre[1], x);

操作五：删除第 $k$ 个插入的数。

先来看如何删除编号为 $k$ 的数。

首先执行 nxt[pre[k]] = nxt[k] 将 $k$ 前面的节点指向 $k$ 后面的节点，再执行 pre[nxt[k]] = pre[k] 将 $k$ 后面的节点指向 $k$ 前面的节点。

void remove(int k) {
    nxt[pre[k]] = nxt[k];
    pre[nxt[k]] = pre[k];
}

由于第 $k$ 个插入的数的编号为 $k + 1$ ，故实现操作五需要这样调用

remove(k + 1);

操作六：输出链表。

从头节点 nxt[0] 遍历到尾节点 pre[1] 即可。

for (int i = nxt[0]; i != 1; i = nxt[i]) cout << val[i] << ' ';

⚠️ 在实现单链表的插入操作时，形参 k 的意义是「第 $k$ 个插入的数」，而在实现双链表的插入操作时，为方便理解，形参 k 的意义变成了「编号为 $k$ 的数」。事实上，前者可以采用后者的形参意义进行实现，后者也可以采用前者的形参意义进行实现。

二、用数组实现栈

有了用数组实现链表的经验后，用数组实现栈就变得非常简单了。

class Stack {
private:
    int stk[N], idx;  // idx始终指向栈顶元素

public:
    Stack() : idx(0) {}

    void push(int x) {
        stk[++idx] = x;
    }

    void pop() {
        idx--;
    }

    int top() {
        return stk[idx];
    }

    bool empty() {
        return idx == 0;
    }

    int size() {
        return idx;
    }
};

三、用数组实现队列

设置两个指针 ql 和 qr，其中 ql 始终指向队头元素，qr 始终指向队尾元素。

class Queue {
private:
    int q[N], ql, qr;

public:
    Queue() : ql(1), qr(0) {}

    void push(int x) {
        q[++qr] = x;
    }

    void pop() {
        ql++;
    }

    int front() {
        return q[ql];
    }

    int back() {
        return q[qr];
    }

    bool empty() {
        return ql > qr;
    }

    int size() {
        return qr - ql + 1;
    }
};