在第4章，我们审视了R中基本的数据集处理方法，本章我们将关注一些高级话题。本章分为三个基本部分。在第一部分中，我们将快速浏览R中的多种数学、统计和字符处理函数。为了让这一部分的内容相互关联，我们先引入一个能够使用这些函数解决的数据处理问题。在讲解过这些函数以后，再为这个数据处理问题提供一个可能的解决方案。
接下来，我们将讲解如何自己编写函数来完成数据处理和分析任务。首先，我们将探索控制程序流程的多种方式，包括循环和条件执行语句。然后，我们将研究用户自编函数的结构，以及在编写完成后如何调用它们。
最后，我们将了解数据的整合和概述方法，以及数据集的重塑和重构方法。在整合数据时，你可以使用任何内建或自编函数来获取数据的概述，所以你在本章前两部分中学习的内容将会派上用场。

5.1 一个数据处理难题

要讨论数值和字符处理函数，让我们首先考虑一个数据处理问题。一组学生参加了数学、科学和英语考试。为了给所有学生确定一个单一的成绩衡量指标，需要将这些科目的成绩组合起来。另外，你还想将前20%的学生评定为A，接下来20%的学生评定为B，依次类推。最后，你希望按字母顺序对学生排序。数据如表5-1所示。

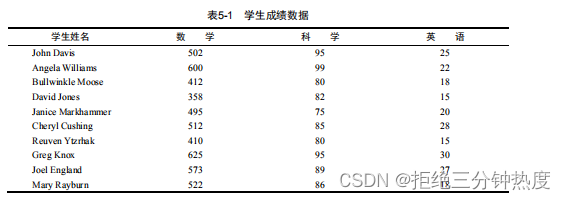
观察此数据集，马上可以发现一些明显的障碍。首先，三科考试的成绩是无法比较的。由于它们的均值和标准差相去甚远，所以对它们求平均值是没有意义的。你在组合这些考试成绩之前，必须将其变换为可比较的单元。其次，为了评定等级，你需要一种方法来确定某个学生在前述得分上百分比排名。再次，表示姓名的字段只有一个，这让排序任务复杂化了。为了正确地将其排序，需要将姓和名拆开。
以上每一个任务都可以巧妙地利用R中的数值和字符处理函数完成。在讲解完下一节中的各种函数之后，我们将考虑一套可行的解决方案，以解决这项数据处理难题。

5.2 数值和字符处理函数

本节我们将综述R中作为数据处理基石的函数，它们可分为数值（数学、统计、概率）函数和字符处理函数。在阐述过每一类函数以后，我将为你展示如何将函数应用到矩阵和数据框的列（变量）和行（观测）上（参见5.2.6节）。

5.2.1 数学函数

表5-2列出了常用的数学函数和简短的用例。


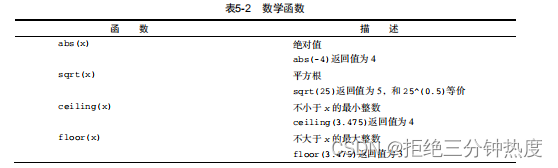
对数据做变换是这些函数的一个主要用途。例如，你经常会在进一步分析之前将收入这种存在明显偏倚的变量取对数。数学函数也被用作公式中的一部分，用于绘图函数（例如x对sin(x)）和在输出结果之前对数值做格式化。
表5-2中的示例将数学函数应用到了标量（单独的数值）上。当这些函数被应用于数值向量、矩阵或数据框时，它们会作用于每一个独立的值。例如，sqrt(c(4, 16, 25))的返回值为c(2, 4, 5)。

5.2.2 统计函数

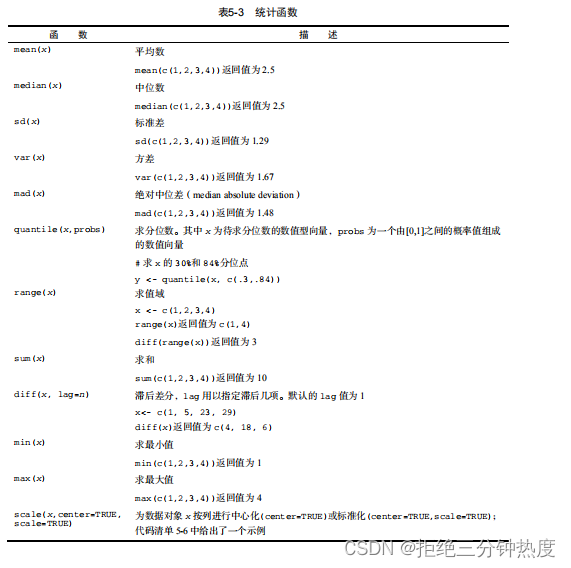
常用的统计函数如表5-3所示，其中许多函数都拥有可以影响输出结果的可选参数。举例
来说：

y <- mean(x)

提供了对象x中元素的算术平均数，而：

z <- mean(x, trim = 0.05, na.rm=TRUE)

则提供了截尾平均数，即丢弃了最大5%和最小5%的数据和所有缺失值后的算术平均数。请使用help()了解以上每个函数和其参数的用法。

要了解这些函数的实战应用，请参考代码清单5-1。这个例子演示了计算某个数值向量的均值和标准差的两种方式。
代码清单5-1 均值和标准差的计算
方法1：

x <- c(1,2,3,4,5,6,7,8)
mean(x)
sd(x)

方法2：

n <- length(x) 
meanx <- sum(x)/n 
css <- sum((x - meanx)^2)
sdx <- sqrt(css / (n-1))
meanx

第二种方式中修正平方和（css）的计算过程是很有启发性的：
(1) x等于c(1, 2, 3, 4, 5, 6, 7, 8)，x的平均值等于4.5（length(x)返回了x中元素
的数量）；
(2) (x – meanx)从x的每个元素中减去了4.5，结果为c(-3.5, -2.5, -1.5, -0.5, 0.5,
1.5, 2.5, 3.5)；
(3) (x – meanx)^2将(x - meanx)的每个元素求平方，结果为c(12.25, 6.25, 2.25,
0.25, 0.25, 2.25, 6.25, 12.25)；
(4) sum((x - meanx)^2)对(x - meanx)^2)的所有元素求和，结果为42。 R中公式的写法和类似MATLAB的矩阵运算语言有着许多共同之处。（我们将在附录D中具体关注解决矩阵代数问题的方法。）

5.2.3 概率函数

你可能在疑惑为何概率函数未和统计函数列在一起。（你真的对此有些困惑，对吧？）虽然根据定义，概率函数也属于统计类，但是它们非常独特，应独立设一节进行讲解。概率函数通常用来生成特征已知的模拟数据，以及在用户编写的统计函数中计算概率值。
在R中，概率函数形如 ：

[dpqr]distribution_abbreviation()

其中第一个字母表示其所指分布的某一方面：
d = 密度函数（density）
p = 分布函数（distribution function）
q = 分位数函数（quantile function）
r = 生成随机数（随机偏差）
常用的概率函数列于表5-4中。

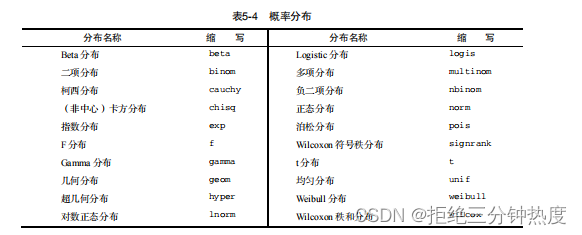
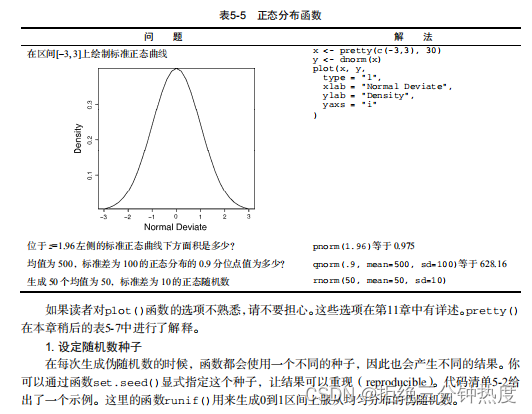
我们不妨先看看正态分布的有关函数，以了解这些函数的使用方法。如果不指定一个均值和一个标准差，则函数将假定其为标准正态分布（均值为0，标准差为1）。密度函数（dnorm）、分布函数（pnorm）、分位数函数（qnorm）和随机数生成函数（rnorm）的使用示例见表5-5。

代码清单5-2 生成服从正态分布的伪随机数

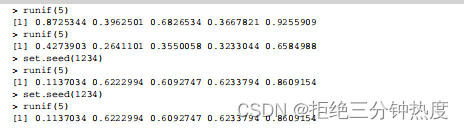
通过手动设定种子，就可以重现你的结果了。这种能力有助于我们创建会在未来取用的，以及可与他人分享的示例。

mvrnorm(n, mean, sigma)

其中n是你想要的样本大小，mean为均值向量，而sigma是方差协方差矩阵（或相关矩阵）。代码清单5-3从一个参数如下所示的三元正态分布中抽取500个观测。

代码清单5-3 生成服从多元正态分布的数据

rm(list = ls()) 
library(MASS)
options(digits=3)
set.seed(1234) # 设定随机种子点
mean <- c(230.7, 146.7, 3.6)
sigma <- matrix(c(15360.8, 6721.2, -47.1, 
                  6721.2, 4700.9, -16.5, 
                  -47.1, -16.5, 0.3), nrow=3, ncol=3)#指定均值向量，协方差阵
mydata <- mvrnorm(500, mean, sigma)# 生成数据
mydata <- as.data.frame(mydata)
names(mydata) <- c("y","x1","x2")
dim(mydata)
head(mydata, n=10)

代码清单5-3中设定了一个随机数种子，这样就可以在之后重现结果➊。你指定了想要的均值向量和方差协方差阵➋，并生成了500个伪随机观测➌。为了方便，结果从矩阵转换为数据框，并为变量指定了名称。最后，你确认了拥有500个观测和3个变量，并输出了前10个观测➍。请注意，由于相关矩阵同时也是协方差阵，所以其实可以直接指定相关关系的结构。
R中的概率函数允许生成模拟数据，这些数据是从服从已知特征的概率分布中抽样而得的。近年来，依赖于模拟数据的统计方法呈指数级增长，在后续各章中会有若干示例。

5.2.4 字符处理函数

数学和统计函数是用来处理数值型数据的，而字符处理函数可以从文本型数据中抽取信息，或者为打印输出和生成报告重设文本的格式。举例来说，你可能希望将某人的姓和名连接在一起，并保证姓和名的首字母大写，抑或想统计可自由回答的调查反馈信息中含有秽语的实例（instance）数量。一些最有用的字符处理函数见表5-6。

请注意，函数grep()、sub()和strsplit()能够搜索某个文本字符串（fixed=TRUE）或
某个正则表达式（fixed=FALSE，默认值为FALSE）。正则表达式为文本模式的匹配提供了一套清晰而简练的语法。例如，正则表达式：

^[hc]?at

可匹配任意以0个或1个h或c开头、后接at的字符串。因此，此表达式可以匹配hat、cat和at，但不会匹配bat。要了解更多，请参考维基百科的regular expression（正则表达式）条目。

5.2.5 其他实用函数

表5-7中的函数对于数据管理和处理同样非常实用，只是它们无法清楚地划入其他分类中。

表中的最后一个例子演示了在输出时转义字符的使用方法。\n表示新行，\t为制表符，’
为单引号，\b为退格，等等。（键入?Quotes以了解更多。）例如，代码：

name <- "Bob" 
cat( "Hello", name, "\b.\n", "Isn\'t R", "\t", "GREAT?\n")

可生成：

Hello Bob. 
 Isn't R GREAT?

请注意第二行缩进了一个空格。当cat输出连接后的对象时，它会将每一个对象都用空格分开。这就是在句号之前使用退格转义字符（\b）的原因。不然，生成的结果将是“Hello Bob .”。
在数值、字符串和向量上使用我们最近学习的函数是直观而明确的，但是如何将它们应用到矩阵和数据框上呢？这就是下一节的主题

5.2.6 将函数应用于矩阵和数据框

R函数的诸多有趣特性之一，就是它们可以应用到一系列的数据对象上，包括标量、向量、矩阵、数组和数据框。代码清单5-4提供了一个示例。
代码清单5-4 将函数应用于数据对象

 a <- 5 
 sqrt(a) 
 b <- c(1.243, 5.654, 2.99) 
 round(b) 
 c <- matrix(runif(12), nrow=3) 
 c 
 log(c) 
mean(c) 

请注意，在代码清单5-4中对矩阵c求均值的结果为一个标量（0.444）。函数mean()求得的是矩阵中全部12个元素的均值。但如果希望求的是各行的均值或各列的均值呢？
R中提供了一个apply()函数，可将一个任意函数“应用”到矩阵、数组、数据框的任何维
度上。apply()函数的使用格式为：

apply(x, MARGIN, FUN, ...)

其中，x为数据对象，MARGIN是维度的下标，FUN是由你指定的函数，而…则包括了任何想传递给FUN的参数。在矩阵或数据框中，MARGIN=1表示行，MARGIN=2表示列。请看以下例子。
代码清单5-5 将一个函数应用到矩阵的所有行（列）

rm(list = ls()) 
mydata <- matrix(rnorm(30), nrow=6) #生成数据
mydata
apply(mydata, 1, mean)#计算每行的均值
apply(mydata, 2, mean)#计算每列的均值
apply(mydata, 2, mean, trim=0.2)# 计算每列的截尾值

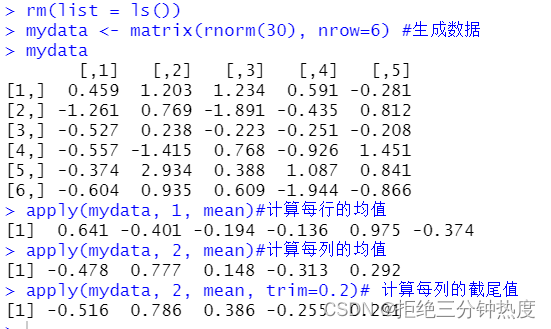
首先生成了一个包含正态随机数的6×5矩阵➊。然后你计算了6行的均值➋，以及5列的均值➌。最后，你计算了每列的截尾均值（在本例中，截尾均值基于中间60%的数据，最高和最低20%的值均被忽略）➍。
FUN可为任意R函数，这也包括你自行编写的函数（参见5.4节），所以apply()是一种很强大的机制。apply()可把函数应用到数组的某个维度上，而lapply()和sapply()则可将函数应用到列表（list）上。你将在下一节中看到sapply()（它是lapply()的更好用的版本）的一个示例。
你已经拥有了解决5.1节中数据处理问题所需的所有工具，现在，让我们小试身手。

5.3 数据处理难题的一套解决方案

5.1节中提出的问题是：将学生的各科考试成绩组合为单一的成绩衡量指标，基于相对名次前20%、下20%、等等）给出从A到F的评分，根据学生姓氏和名字的首字母对花名册进行排序。代码清单5-6给出了一种解决方案。
代码清单5-6 示例的一种解决方案


以上代码写得比较紧凑，逐步分解如下。
步骤1 原始的学生花名册已经给出了。*options(digits=2)*限定了输出小数点后数字的
位数，并且让输出更容易阅读：

步骤2 由于数学、科学和英语考试的分值不同（均值和标准差相去甚远），在组合之前需要先让它们变得可以比较。一种方法是将变量进行标准化，这样每科考试的成绩就都是用单位标准差来表示，而不是以原始的尺度来表示了。这个过程可以使用scale()函数来实现：

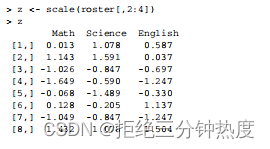
步骤3 然后，可以通过函数mean()来计算各行的均值以获得综合得分，并使用函数
cbind()将其添加到花名册中：

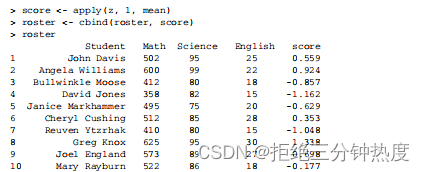
步骤4 函数quantile()给出了学生综合得分的百分位数。可以看到，成绩为A的分界点为0.74，B的分界点为0.44，等等。

步骤5 通过使用逻辑运算符，你可以将学生的百分位数排名重编码为一个新的类别型成绩变量。下面在数据框roster中创建了变量grade。

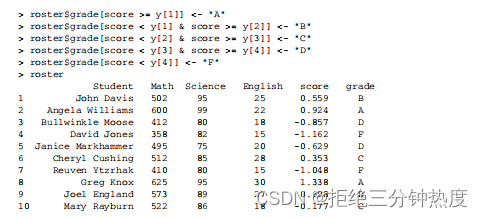
步骤6 你将使用函数strsplit()以空格为界把学生姓名拆分为姓氏和名字。把
strsplit()应用到一个字符串组成的向量上会返回一个列表：

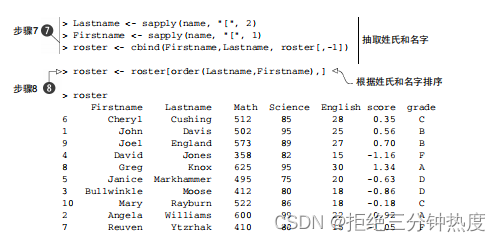
步骤7 你可以使用函数sapply()提取列表中每个成分的第一个元素，放入一个储存名字的向量Firstname，并提取每个成分的第二个元素，放入一个储存姓氏的向量Lastname。"["是一个可以提取某个对象的一部分的函数——在这里它是用来提取列表name各成分中的第一个或第二个元素的。你将使用cbind()把它们添加到花名册中。由于已经不再需要student变量，可以将其丢弃（在下标中使用–1）。

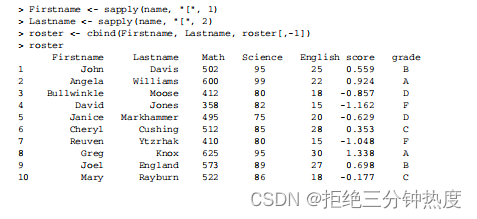
步骤8 最后，可以使用函数order()依姓氏和名字对数据集进行排序：

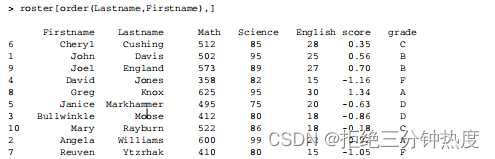
瞧！小事一桩！
完成这些任务的方式有许多，只是以上代码体现了相应函数的设计初衷。现在到学习控制结构和自己编写函数的时候了。

5.4 控制流

在正常情况下，R程序中的语句是从上至下顺序执行的。但有时你可能希望重复执行某些语句，仅在满足特定条件的情况下执行另外的语句。这就是控制流结构发挥作用的地方了。
R拥有一般现代编程语言中都有的标准控制结构。首先你将看到用于条件执行的结构，接下来是用于循环执行的结构。
为了理解贯穿本节的语法示例，请牢记以下概念：
 语句（statement）是一条单独的R语句或一组复合语句（包含在花括号{ }中的一组R
语句，使用分号分隔）；
 条件（cond）是一条最终被解析为真（TRUE）或假（FALSE）的表达式；
 表达式（expr）是一条数值或字符串的求值语句；
 序列（seq）是一个数值或字符串序列。
在讨论过控制流的构造后，我们将学习如何编写函数。

5.4.1 重复和循环

循环结构重复地执行一个或一系列语句，直到某个条件不为真为止。循环结构包括for和
while结构。
1. for结构
for循环重复地执行一个语句，直到某个变量的值不再包含在序列seq中为止。语法为：

for (var in seq) statement

在下例中：

for (i in 1:10) print("Hello")

单词Hello被输出了10次。
2. while结构
while循环重复地执行一个语句，直到条件不为真为止。语法为：

while (cond) statement

作为第二个例子，代码：

i <- 10 
while (i > 0) {print("Hello"); i <- i - 1}

又将单词Hello输出了10次。请确保括号内while的条件语句能够改变，即让它在某个时刻不再为真——否则循环将永不停止！在上例中，语句：

i <- i – 1

在每步循环中为对象i减去1，这样在十次循环过后，它就不再大于0了。反之，如果在每步循环都加1的话，R将不停地打招呼。这也是while循环可能较其他循环结构更危险的原因。
在处理大数据集中的行和列时，R中的循环可能比较低效费时。只要可能，最好联用R中的内建数值/字符处理函数和apply族函数。

5.4.2 条件执行

在条件执行结构中，一条或一组语句仅在满足一个指定条件时执行。条件执行结构包括
if-else、ifelse和switch。
1. if-else结构
控制结构if-else在某个给定条件为真时执行语句。也可以同时在条件为假时执行另外的语句。语法为：

if (cond) statement
if (cond) statement1 else statement2

示例如下：

if (is.character(grade)) grade <- as.factor(grade) 
if (!is.factor(grade)) grade <- as.factor(grade) else print("Grade already  is a factor")

在第一个实例中，如果grade是一个字符向量，它就会被转换为一个因子。在第二个实例中，两个语句择其一执行。如果grade不是一个因子（注意符号!），它就会被转换为一个因子。如果它是一个因子，就会输出一段信息。
2. ifelse结构
ifelse结构是if-else结构比较紧凑的向量化版本，其语法为：

ifelse(cond, statement1, statement2)

若cond为TRUE，则执行第一个语句；若cond为FALSE，则执行第二个语句。示例如下：

ifelse(score > 0.5, print("Passed"), print("Failed")) 
outcome <- ifelse (score > 0.5, "Passed", "Failed")

在程序的行为是二元时，或者希望结构的输入和输出均为向量时，请使用ifelse
3. switch结构
switch根据一个表达式的值选择语句执行。语法为：

switch(expr, ...)

其中的…表示与expr的各种可能输出值绑定的语句。通过观察代码清单5-7中的代码，可以轻松地理解switch的工作原理。
代码清单5-7 一个switch示例

5.5 用户自编函数

R的最大优点之一就是用户可以自行添加函数。事实上，R中的许多函数都是由已有函数构成的。一个函数的结构看起来大致如此：

myfunction <- function(arg1, arg2, ... ){ 
 statements 
 return(object) 
}

函数中的对象只在函数内部使用。返回对象的数据类型是任意的，从标量到列表皆可。让我们看一个示例。
假设你想编写一个函数，用来计算数据对象的集中趋势和散布情况。此函数应当可以选择性地给出参数统计量（均值和标准差）和非参数统计量（中位数和绝对中位差）。结果应当以一个含名称列表的形式给出。另外，用户应当可以选择是否自动输出结果。除非另外指定，否则此函数的默认行为应当是计算参数统计量并且不输出结果。代码清单5-8给出了一种解答。
代码清单5-8 mystats()：一个由用户编写的描述性统计量计算函数

if (parametric) { 
 center <- mean(x); spread <- sd(x) 
 } else { 
 center <- median(x); spread <- mad(x) 
 } 
 if (print & parametric) { 
 cat("Mean=", center, "\n", "SD=", spread, "\n") 
 } else if (print & !parametric) { 
 cat("Median=", center, "\n", "MAD=", spread, "\n") 
 } 
 result <- list(center=center, spread=spread) 
 return(result) 
}

要看此函数的实战情况，首先需要生成一些数据（服从正态分布的，大小为500的随机样本）：

set.seed(1234) 
x <- rnorm(500)

在执行语句：

y <- mystats(x)

之后，y$center将包含均值（0.00184），y$spread将包含标准差（1.03），并且没有输出结果。
如果执行语句：

y <- mystats(x, parametric=FALSE, print=TRUE)

y$center将包含中位数（–0.0207），y$spread将包含绝对中位差（1.001）。另外，还会输出以下结果：

Median= -0.0207 
MAD= 1

下面让我们看一个使用了switch结构的用户自编函数，此函数可让用户选择输出当天日期的格式。在函数声明中为参数指定的值将作为其默认值。在函数mydate()中，如果未指定type， 则long将为默认的日期格式：

mydate <- function(type="long") { 
 switch(type, 
 long = format(Sys.time(), "%A %B %d %Y"), 
 short = format(Sys.time(), "%m-%d-%y"), 
 cat(type, "is not a recognized type\n") 
 ) 
}

实战中的函数如下：

mydate(“long”)
[1] “Monday July 14 2014”
mydate(“short”)
[1] “07-14-14”
mydate()
[1] “Monday July 14 2014”
mydate(“medium”)
medium is not a recognized type
请注意，函数cat()仅会在输入的日期格式类型不匹配"long"或"short"时执行。使用一
个表达式来捕获用户的错误输入的参数值通常来说是一个好主意。
有若干函数可以用来为函数添加错误捕获和纠正功能。你可以使用函数warning()来生成一条错误提示信息，用message()来生成一条诊断信息，或用stop()停止当前表达式的执行并提示错误。20.5节将会更加详细地讨论错误捕捉和调试。
在创建好自己的函数以后，你可能希望在每个会话中都能直接使用它们。附录B描述了如何定制R环境，以使R启动时自动读取用户编写的函数。我们将在第6章和第8章中看到更多的用户自编函数示例。
你可以使用本节中提供的基本技术完成很多工作。第20章的内容更加详细地涵盖了控制流和其他编程主题。第21章涵盖了如何创建包。如果你想要探索编写函数的微妙之处，或编写可以分发给他人使用的专业级代码，个人推荐阅读这两章，然后阅读两本优秀的书籍，你可在本书末尾的参考文献部分找到：Venables & Ripley（2000）以及Chambers（2008）。这两本书共同提供了大量细节和众多示例。
函数的编写就讲到这里，我们将以对数据整合和重塑的讨论来结束本章。

5.6 整合与重构

R中提供了许多用来整合（aggregate）和重塑（reshape）数据的强大方法。在整合数据时，往往将多组观测替换为根据这些观测计算的描述性统计量。在重塑数据时，则会通过修改数据的结构（行和列）来决定数据的组织方式。本节描述了用来完成这些任务的多种方式。
在接下来的两个小节中，我们将使用已包含在R基本安装中的数据框mtcars。这个数据集是从Motor Trend杂志（1974）提取的，它描述了34种车型的设计和性能特点（汽缸数、排量、马力、每加仑汽油行驶的英里数，等等）。要了解此数据集的更多信息，请参阅help(mtcars)。

5.6.1 转置

转置（反转行和列）也许是重塑数据集的众多方法中最简单的一个了。使用函数t()即可
对一个矩阵或数据框进行转置。对于后者，行名将成为变量（列）名。代码清单5-9展示了一个例子。
代码清单5-9 数据集的转置

为了节约空间，代码清单5-9仅使用了mtcars数据集的一个子集。在本节稍后讲解reshape2包的时候，你将看到一种更为灵活的数据转置方式。

5.6.2 整合数据

在R中使用一个或多个by变量和一个预先定义好的函数来折叠（collapse）数据是比较容易的。调用格式为：

aggregate(x, by, FUN)

其中x是待折叠的数据对象，by是一个变量名组成的列表，这些变量将被去掉以形成新的观测，而FUN则是用来计算描述性统计量的标量函数，它将被用来计算新观测中的值。
作为一个示例，我们将根据汽缸数和挡位数整合mtcars数据，并返回各个数值型变量的均值（见代码清单5-10）。
代码清单5-10 整合数据

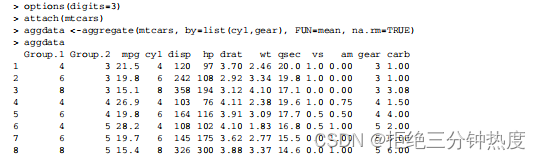
在结果中，Group.1表示汽缸数量（4、6或8），Group.2代表挡位数（3、4或5）。举例来说，拥有4个汽缸和3个挡位车型的每加仑汽油行驶英里数（mpg）均值为21.5。
在使用aggregate()函数的时候，by中的变量必须在一个列表中（即使只有一个变量）。你可以在列表中为各组声明自定义的名称，例如 by=list(Group.cyl=cyl, Group.
gears=gear)。指定的函数可为任意的内建或自编函数，这就为整合命令赋予了强大的力量。但说到力量，没有什么可以比reshape2包更强。

5.7 小结

本章总结了数十种用于处理数据的数学、统计和概率函数。我们看到了如何将这些函数应用到范围广泛的数据对象上，其中包括向量、矩阵和数据框。你学习了控制流结构的使用方法：用循环重复执行某些语句，或用分支在满足某些特定条件时执行另外的语句。然后你编写了自己的函数，并将它们应用到数据上。最后，我们探索了折叠、整合以及重构数据的多种方法。
既然已经集齐了数据塑形（没有别的意思）所需的工具，你就准备好告别第一部分并进入激动人心的数据分析世界了！在接下来的几章中，我们将探索多种将数据转化为信息的统计方法和图形方法。

6.参考来源