注：本文为第2章谱域图卷积介绍视频笔记，仅供个人学习使用

---

---

1、图卷积简介

1.1 图卷积网络的迅猛发展

• 16年以前，每年只有1-2篇相关文献

• 18年，有些会议上大概有了7-8篇

• 19年，文章数量爆炸性增长，仅仅NIPS一个会议就有49篇文章

1.2 回顾，经典卷积神经网络已在多个领域取得成功

1.3 两大类数据

规则数据（欧氏空间）	不规则数据（非欧氏空间）
语音：一维向量；图像：二维矩阵；视频：三维矩阵	社交数据 、分子结构 、人体骨架

1.4 经典卷积神经网络的局限：无法处理图数据结构

经典卷积处理图结构数据的局限：

• 只能处理固定输入维度的数据
• 局部输入必须有序

1.5 将卷积扩展到图结构数据中

1. 频域：指将信号转换为频率的域，通过对频率的分析来研究信号的频率特性。常用的转换方法是使用傅里叶变换。在频域中，信号可以表示为各个频率分量的相对强度。
2. 谱域：指将信号转换为能量或功率的域，通过对能量或功率的分析来研究信号的能量或功率分布。常用的转换方法是使用功率谱密度函数。在谱域中，信号可以表示为各个频率分量的能量或功率。
3. 空域：指将信号转换为空间坐标的域，通过对空间坐标的分析来研究信号的空间特性。在空域中，信号可以表示为在不同空间位置上的强度。
4. 时域：指将信号转换为时间坐标的域，通过对时间坐标的分析来研究信号的时间特性。在时域中，信号可以表示为在不同时间上的变化。

---

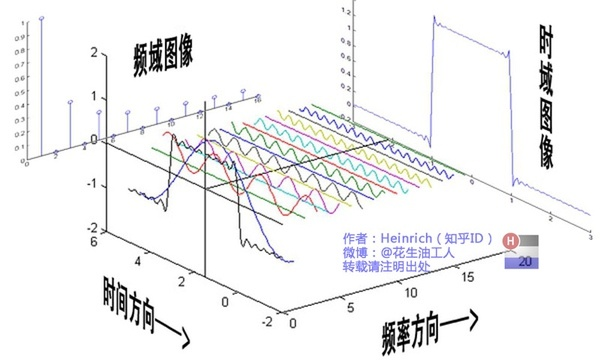
谱域图卷积

• 根据图谱理论和卷积定理，将数据由空域转到谱域做处理

• 有较为坚实的理论基础

空域图卷积

• 不依靠图谱卷积理论，直接在空间上定义卷积操作
• 定义直观，灵活性强

部分经典模型

2、图谱卷积背景知识

2.1 谱域图卷积实现思路

根据卷积定理，两信号在空域（或时域）卷积的傅里叶变换等于这俩个信号在频域中的傅里叶变换的乘积：

也可以通过反变换的形式来表达：

f1(t) 定义为空域输入信号，f2(t)定义为空域卷积核，卷积操作即为：先将空域上的信号f1(t)转换到频域信号F1(w)，f2(t)转换到频域F2(w)，然后将频域信号相乘，再将相乘后的结果通过傅里叶反变换转回空域，这个就是谱域图卷积的实现思路（将空域转换到频域上处理，处理完再返回)。

经典的卷积操作具有序列有序性和维数不变性的限制，使得经典卷积难以处理图数据，对于一个3x3的卷积核，它的形状是固定的，它的感受野的中心节点必须要有固定的邻域大小才能使用卷积核，但是图上的节点的领域节点是不确定的，此外图上节点的领域节点也是没有顺序的，这就不能直接在空域使用经典的卷积。但是当把数据从空域转换到频域，在频域处理数据时，只需要将每个频域的分量放大或者缩小就可以了，不需要考虑信号在空域上存在的问题，这个就是谱域图卷积的核心。

经典傅里叶变换：

基于图谱理论，可以使用图傅里叶变换。

2.2 拉普拉斯矩阵

2.2.1 拉普拉斯算子

拉普拉斯算子△ 的定义为梯度gradient▽的散度divergence▽·。即Δf=▽·(▽f) = div(grad(f))。

对于n维欧式空间，可普遍认为拉普拉斯算子是一个二阶微分算子，即在各个维度求二阶导数后求和。

在3维欧氏空间，对于一个三元函数f(x,y,z)，可以得到

离散情况下欧氏空间的拉普拉斯算子 ，对于两个变量的函数f(x,y)

那么两个变量的离散拉普拉斯算子可以写成：

二维的拉普拉斯算子可以理解为中心节点与周围节点的差值，然后求和。如下图，对于某个中心像素（红色）的算子为周围四个像素之和减去4倍的自己。

类似，在图上的拉普拉斯算子定义：

其中，f = (f1, f2, ···, fn)，代表n个结点上每个结点的信号。

当有权重时：

可以理解为中心节点依次减去周围节点，乘以权重后，然后求和。

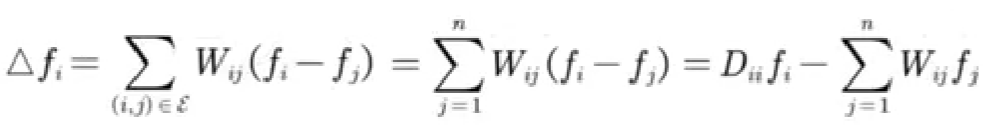
对于n个节点有：

2.2.2 拉普拉斯矩阵

拉普拉斯矩阵是图上的一种拉普拉斯算子。

D为度矩阵，它对角线上的值是从 i 节点出发的所有边的权重之和（nxn的方阵，是对角矩阵）。

拉普拉斯矩阵（L）是度矩阵（D）减去邻接矩阵（W），即L = D - W。

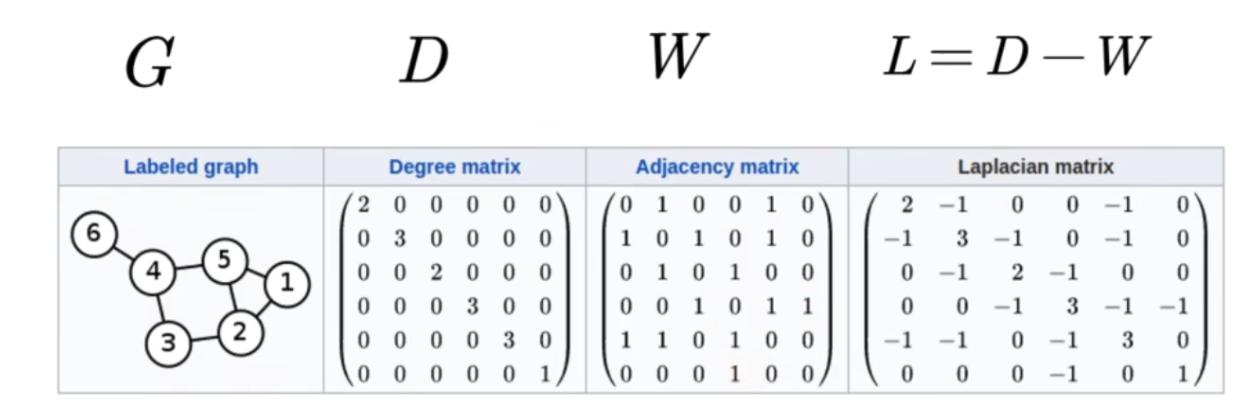
• 性质：拉普拉斯矩阵是对称半正定矩阵，因此该矩阵的特征值一定非负，一定有n个线性无关的特征向量，它们是n维空间中的一组标准正交基，组成正交矩阵。

特征分解（Eigen decomposition），又称谱分解（Spectral decomposition），是将矩阵分解为由其特征值和特征向量表示的矩阵之积的方法。

L是拉普拉斯矩阵，U是拉普拉斯矩阵特征向量组成的矩阵，λ是特征向量，组成对角阵∧。

拉普拉斯矩阵有n个线性无关的特征向量，可以组成n维线性空间中的一组基。

又因为对称矩阵的不同特征值对应的特征向量相互正交，这些正交的特征向量构成的矩阵为正交矩阵。所以拉普拉斯矩阵的n个特征向量是n维空间中的一组标准正交基。

2.3 图傅里叶变换

图上信号的定义：一般表达为一个向量。假设有n个节点，将图上的信号记为：
每一个节点上有一个信号值，节点i上的值为x(i) = xi

下图中蓝色线段代表信号的大小，类似于图像上灰度图像像素，像素越高，画的这个线段越长。

经典傅里叶变换如下

• 傅里叶正变换F：求线性组合的系数。具体做法是由原函数和基函数的共轭的内积求得。
• 傅里叶反变换f：一个信号由不同频率的基函数信号叠加而成，即把任意一个函数表示成了若干个正交基函数的线性组合。

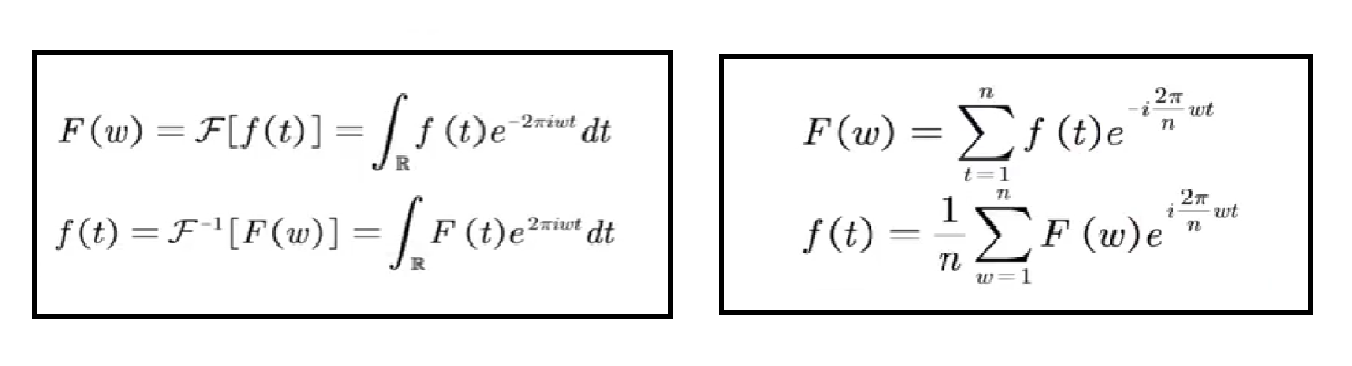
左边为连续空间中的傅里叶变换，右边为离散傅里叶变换。

傅里叶变换的本质是内积，三角函数是完备的正交函数集，不同频率的三角函数的之间的内积为0，只有频率相等的三角函数做内积时，才不为0。

参考自 一文道破傅里叶变换的本质，优缺点一目了然

经典傅里叶变换：一个信号由不同频率的基函数信号叠加而成。左图中红色信号是原信号，蓝色信号是不同频率上的基函数信号（余弦或者正弦函数）。则红色原信号可以由不同频率的基函数线性组合而成，右图蓝色的高度表示基前面的系数，也就是所谓的傅里叶系数，也就是原函数在这个基上的坐标分量。

相位在图中被忽略了，实际上的傅里叶系数包含振幅和相位。

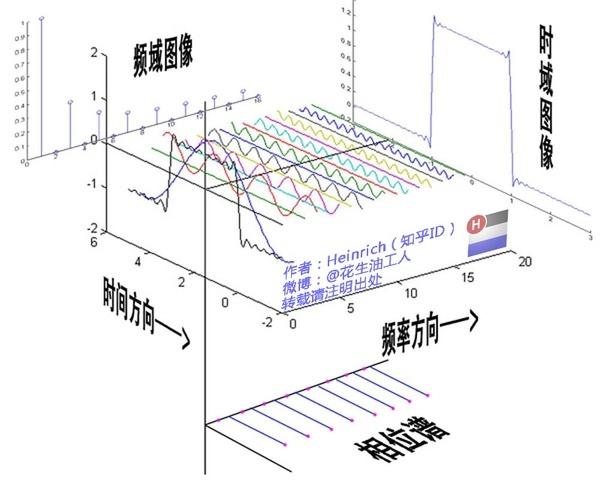
对应经典傅里叶变换的思想，对于图上信号x的傅里叶变换，希望找到一组正交基，通过这组正交基的线性组合来表达x。而拉普拉斯矩阵的特征向量正好是正交的，可以作为图傅里叶变换的基函数。

则傅里叶逆变换可以将图上的信号可以表示为：

小结：依靠图傅里叶变换可以将定义在图上结点上的信号x从空间域与转到谱域。

经典傅里叶变换	图傅里叶变换
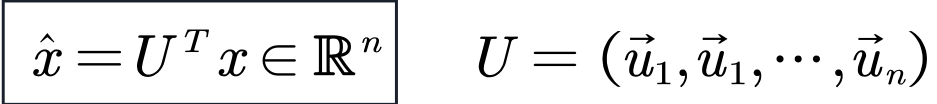基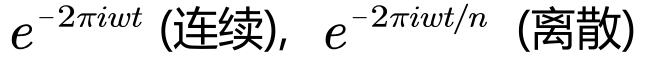：	基：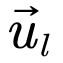
频率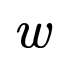：	频率”：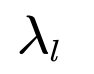
分量的振幅(和相位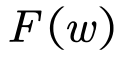）:	分量的振幅: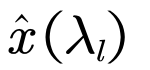

2.4 图卷积定理

图上的卷积定义：先对输入信号 x 和卷积核 g 做傅里叶正变换，然后在谱域上做 harmand 乘积，也就是 F ( x ) ⊙ F ( g ) 。最后通过傅里叶反变换 F^-1 将结果返回到空域。

如果用矩阵乘法的形式来表达这个公式，去掉harmand乘积。同时，通常并不关心空间域上的滤波器信号g是什么样子的，只关心其在频域的情况。令

则公式等价的转换成下式：

所有的谱图卷积都遵循这些定义，唯一的不同就是 滤波器 filter 的选取

3、三个经典图谱卷积模型

简介

• 三个图谱卷积模型（SCNN、ChebNet、GCN）均立足于谱图理论且一脉相承。
• ChebNet可看做SCNN的改进，GCN可看做ChebNet的改进。
• 三个模型均可认为是下式的一个特例。

在卷积前后：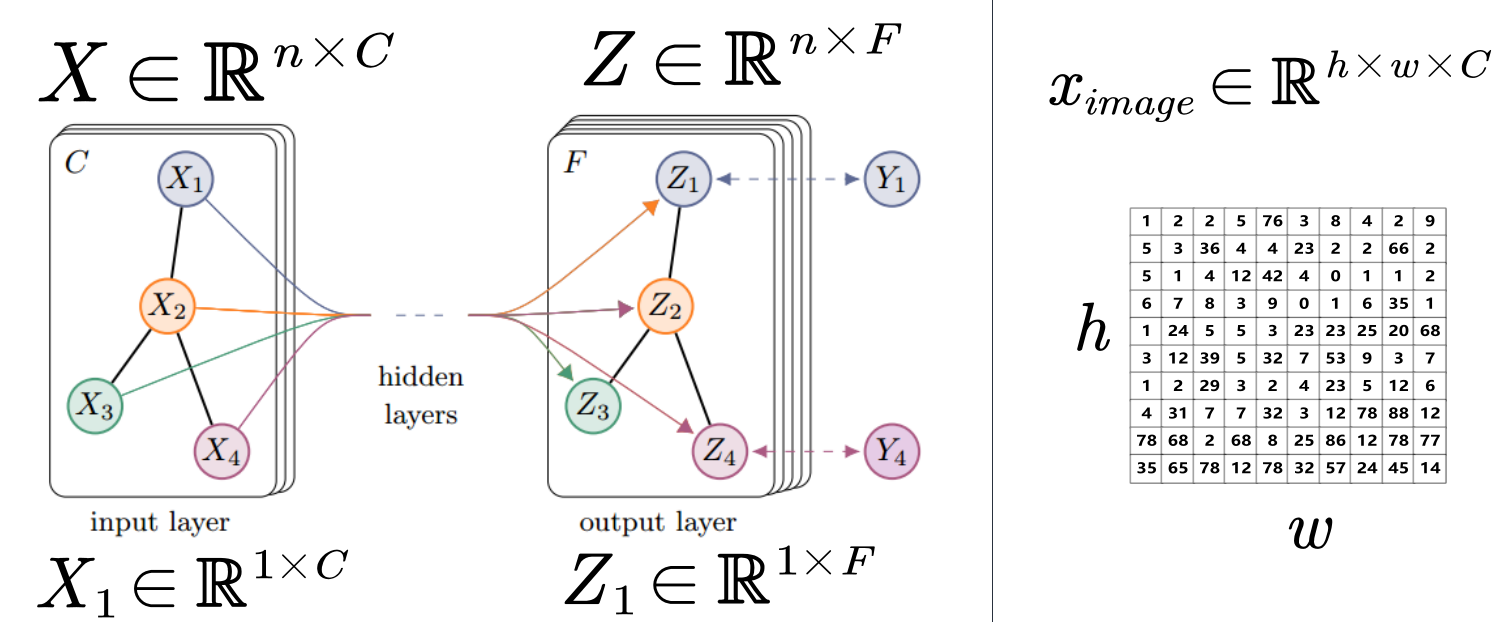
其中，某一层的特征图可以表示为一个 nxc 的矩阵。n代表图中有n个结点，C是通道个数。图中的信号可以分解为各个结点上的信号。X代表整个图上的信号，是nxc 的矩阵，X_i代表某个结点的信号，是一个 1xc 的向量。

在不同层中，特征图结构是不发生变化的，只有图上的信号会发生变化。

---

3.1 SCNN

论文：Spectral networks and locally connected networks on graphs

第一代GCN，文中给出了两个模型，分别是基于空间域的和基于谱域的。基于谱域的模型的核心是用对角矩阵来代替谱域的卷积核

核心思想：用可学习的对角矩阵来代替谱域的卷积核，从而实现图卷积操作。即：

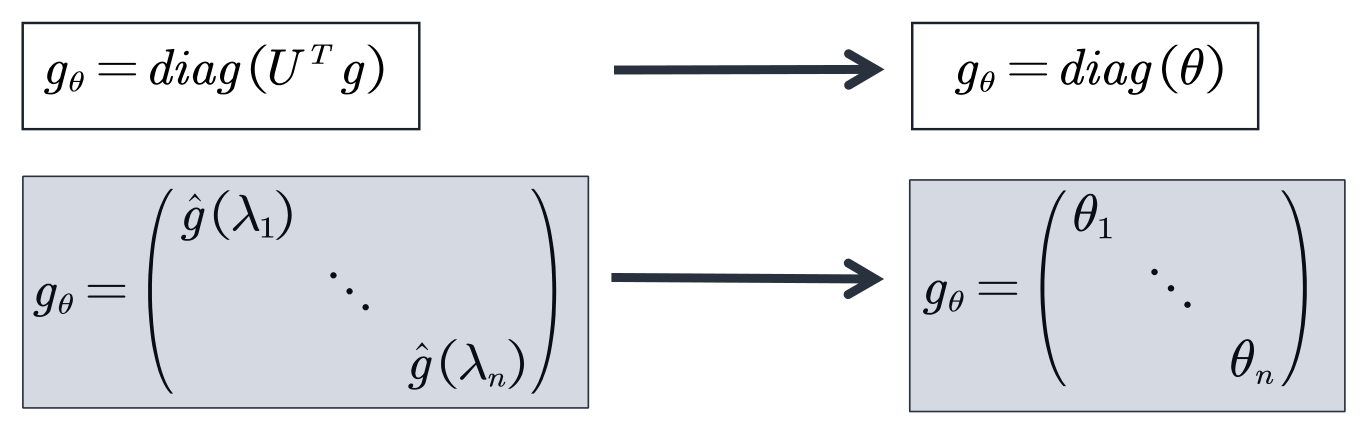
公式定义如下：

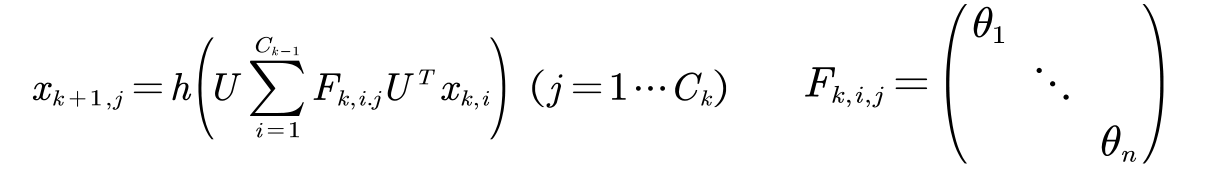
• 其中， C_k表示第k层的channel（通道）个数， x_k,i ∈ Rⁿ表示第k层的第i个channel的 feature map（特征图）
• F_k,i,j 属于 R^nxn 代表参数化的谱域的卷积核矩阵。 它是一个对角矩阵，包含了n个可学习的参数。h(·) 是激活函数。

SCNN的缺点

• 计算拉普拉斯矩阵的特征值分解非常耗时。计算复杂度为O(n³) ，n为节点个数。当处理大规模图数据时（比如社交网络数据，通常有上百万个节点）会面临很大的挑战。
• 模型的参数复杂度较大。计算复杂度为 ，当节点数较多时容易过拟合。
• 无法保证局部链接，因为将频域转为空域后是全局连接。

3.2 ChebNet

论文：Convolutional neural networks on graphs with fast localized spectral filtering

切比雪夫多项式：

在矩阵状态下， 切比雪夫多项式可以表示为：

核心思想：采用切比雪夫多项式近似谱域的filter。

因为切比雪夫多项式在逼近理论中，可以用于多项式插值，也就是说可以利用切比雪夫多项式来逼近函数。

在拟合时，将x的k次方换成了切比雪夫多项式的k阶项，用切比雪夫多项式来进行逼近。如下图：

为什么要替换？当替换后，SCNN中可以省略对于拉普拉斯矩阵的特征值分解这一最耗时的操作，直接使用拉普拉斯矩阵即可

ChebNet特点：

• 卷积核只有K+1个可学习的参数，一般 K远小于n，参数的复杂度被大大降低
• 采用Chebyshev多项式代替谱域的卷积核后，经过推导，ChebNet不需要对拉普拉斯矩阵做特征分解了。省略了最耗时的步骤。
• 卷积核具有严格的空间局部性。同时，K就是卷积核的“感受野半径”。即将中心顶点K阶近邻节点作为邻域节点。

3.3 GCN

论文：Semi-supervised classification with graph convolutional networks

GCN可视为对ChebNet的进一步简化：仅考虑1阶切比雪夫多项式，且每个卷积核仅只有一个参数，所以只有两个参数。

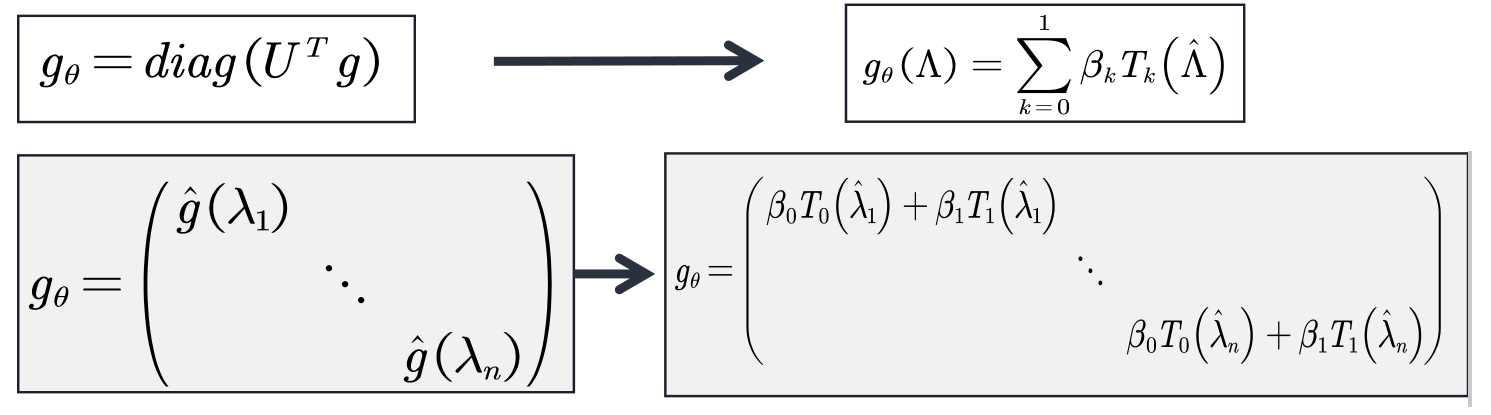
理解：

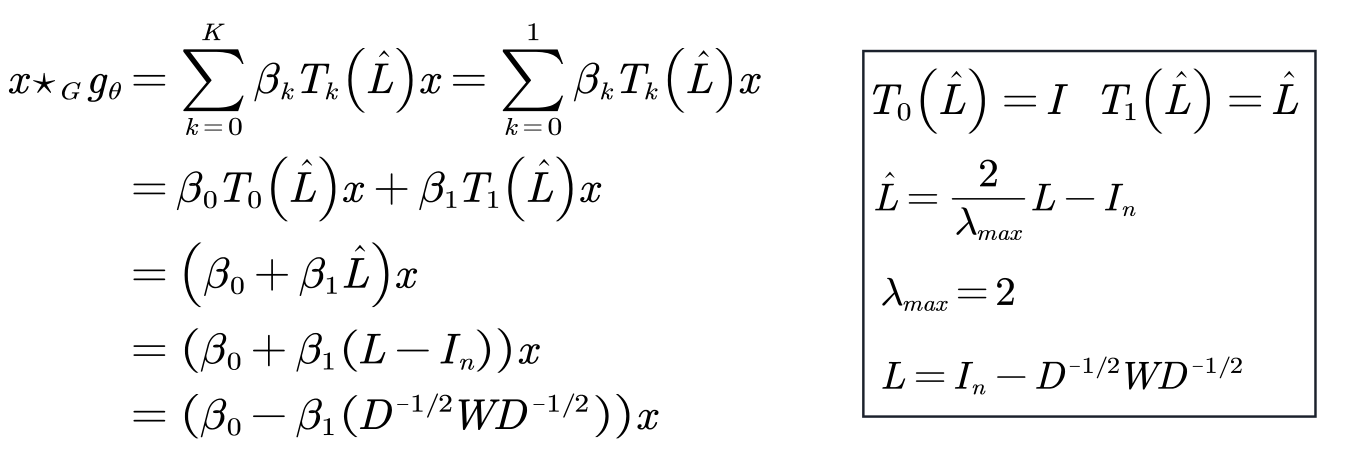
进一步简化，使得每个卷积核只有一个可学习的参数。

因为 有范围[0,2]的特征值，如果在深度神经网络模型中使用该算子，则反复应用该算子会导致数值不稳定（发散）和梯度爆炸/消失，为了解决该问题, 引入了一个 renormalization trick.

从而得到GCN的最终公式

GCN的特点：

• 在忽略input channel 和 output channel的情况下，卷积核只有1个可学习的参数，极大的减少了参数量。（ 按照作者的说法: “We intuitively expect that such a model can alleviate the problem of overfitting on local neighborhood structures for graphs with very wide node degree distributions, such as socialnetworks, citation networks, knowledge graphs and many other real-world graph datasets.”）
• 虽然卷积核大小减少了（GCN仅仅关注于一阶邻域，类似于3X3的经典卷积），但是作者认为通过多层堆叠GCN，仍然可以起到扩大感受野的作用。
• 与此同时，这样极端的参数削减也受到一些人的质疑。他们认为每个卷积核如果只设置一个可学习参数，会降低模型的能力。（可以参考博文How powerful are Graph Convolutions? ）
  • 如果将传统图像的每一个像素视为graph的一个节点，节点之间为八邻域链接，图像也可以看做一张特殊的图。那么在每个3*3的卷积核里，仅仅存在1个可学习的参数。
  • 从目前应用在image的深度学习经验看来，这样的卷积模型复杂度虽然低，但是模型的能力也遭到了削弱，可能难以处理复杂的任务。