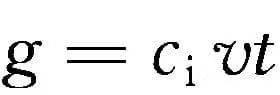一、题目

在这里插入图片描述

二、思路

这道题其实不太容易看出背后的模型。这道题本质上是一个分组背包问题。我们将每一个公司看成一组，而在每一个组内，将不同情况下的盈利状况看作物品的价值，而得到这种利益所需的机器数目看作物品的体积。

因此，这个问题就变成了，从不同的组内，至多选取一个物品，在背包容量允许的条件下，我们所能携带的最大价值。

那么这道题的其中一问就可以解决了。如果大家不懂分组背包的话，建议大家去看作者之前的文章：分组背包问题详解

那么第二个问题是我们今天讨论的重点，即对于背包问题而言，我们如何存储最优解的方案？

此时我们采用拓扑图的角度来理解这个问题，我们求解答案的过程就是构建拓扑图的过程。我们将每个状态看作一个点，然后通过点与点之间的连接体现DP中的状态转移方程。如下图所示：
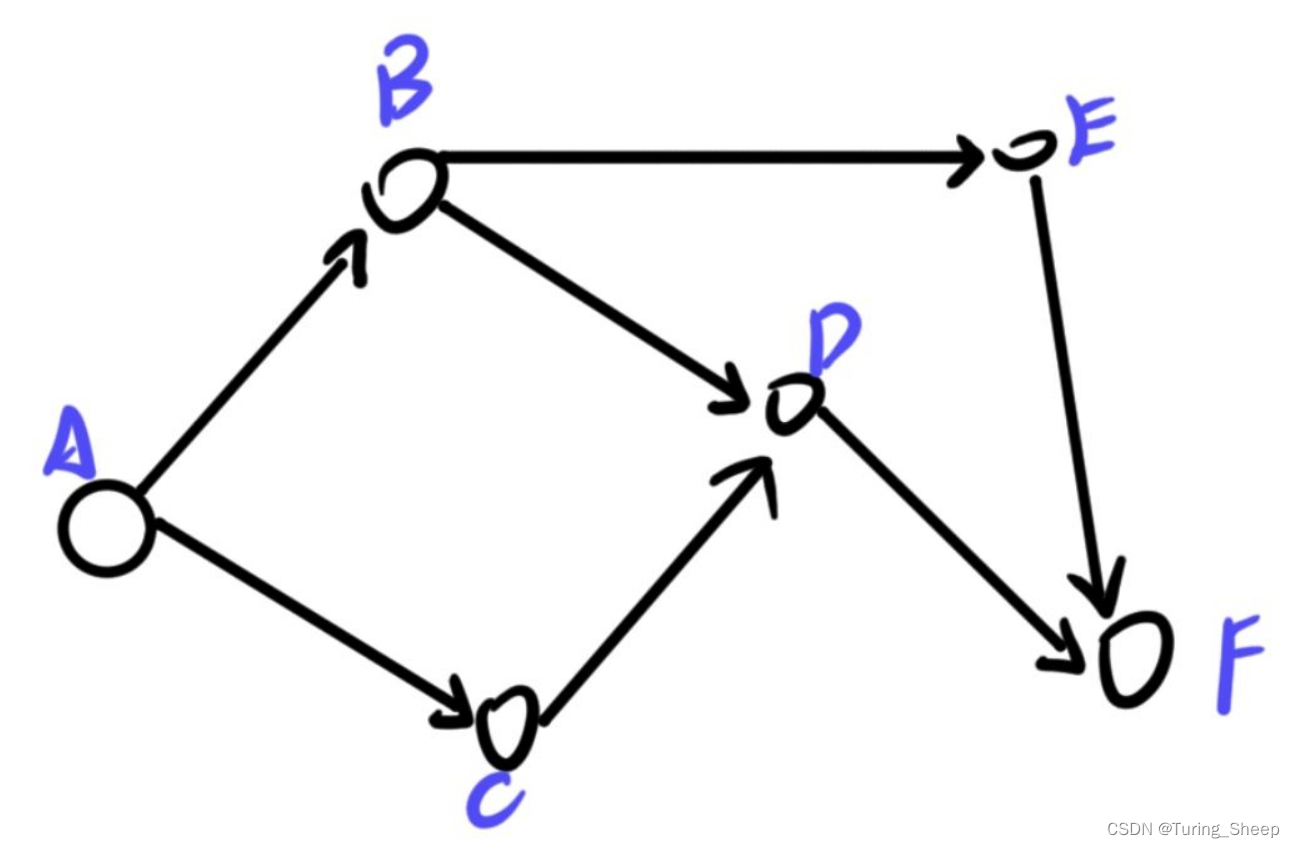在这里插入图片描述 A点就是我们初始化的状态，当我们的得到了A点后，才能够通过转移，即图中的边，得到状态B。

当我们算出了状态B和状态C的时候，才能够通过边的连接得到状态D，状态D到底是什么则需要对比由B和C转移过来的两条路线中哪个是当下的最优解，当比较出最优解后，我们的状态D就可以被赋值为这个最优解。

如果将上述的拓扑图看作一个动态的过程的话，我们会发现这是一个从一个点不断地变成图的过程。

接下来，我们利用上面的图来分析如何得到详细地方案，首先我们想知道到达某个状态的方案，放在这个图里，即我们想知道到达一个点的路线（但并不是所有能到当前的点的路线都是答案，我们需要在这些路线中比较出最优的）。

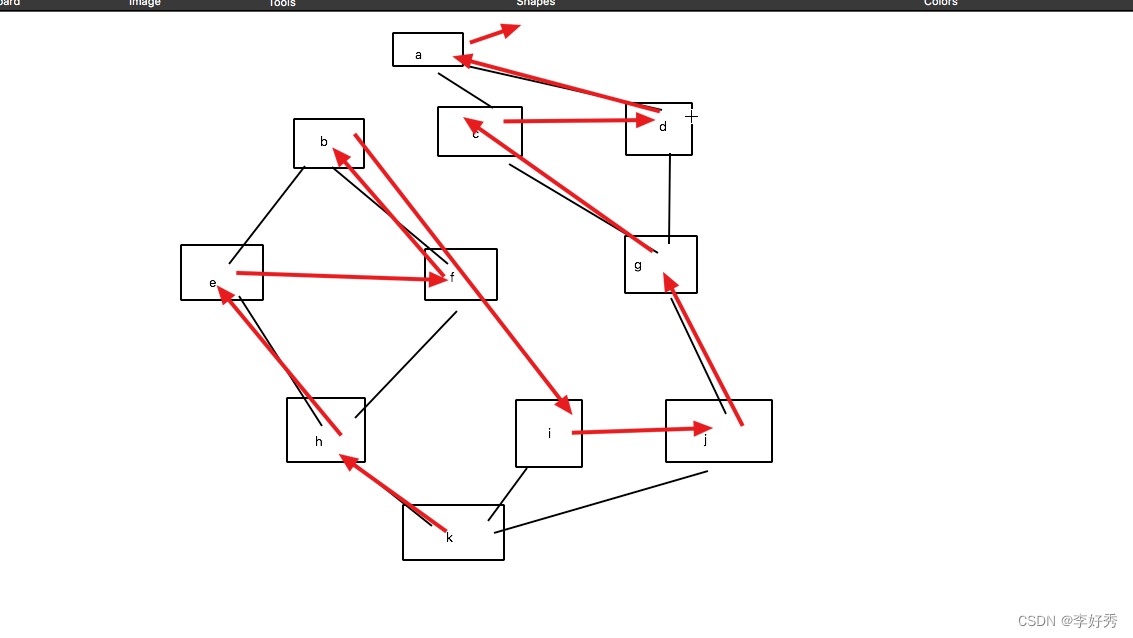
很明显，我们需要先在图中定位到这个点，然后观察它的入度，如下图，假设我们想知道到达F点的最优解的路线：
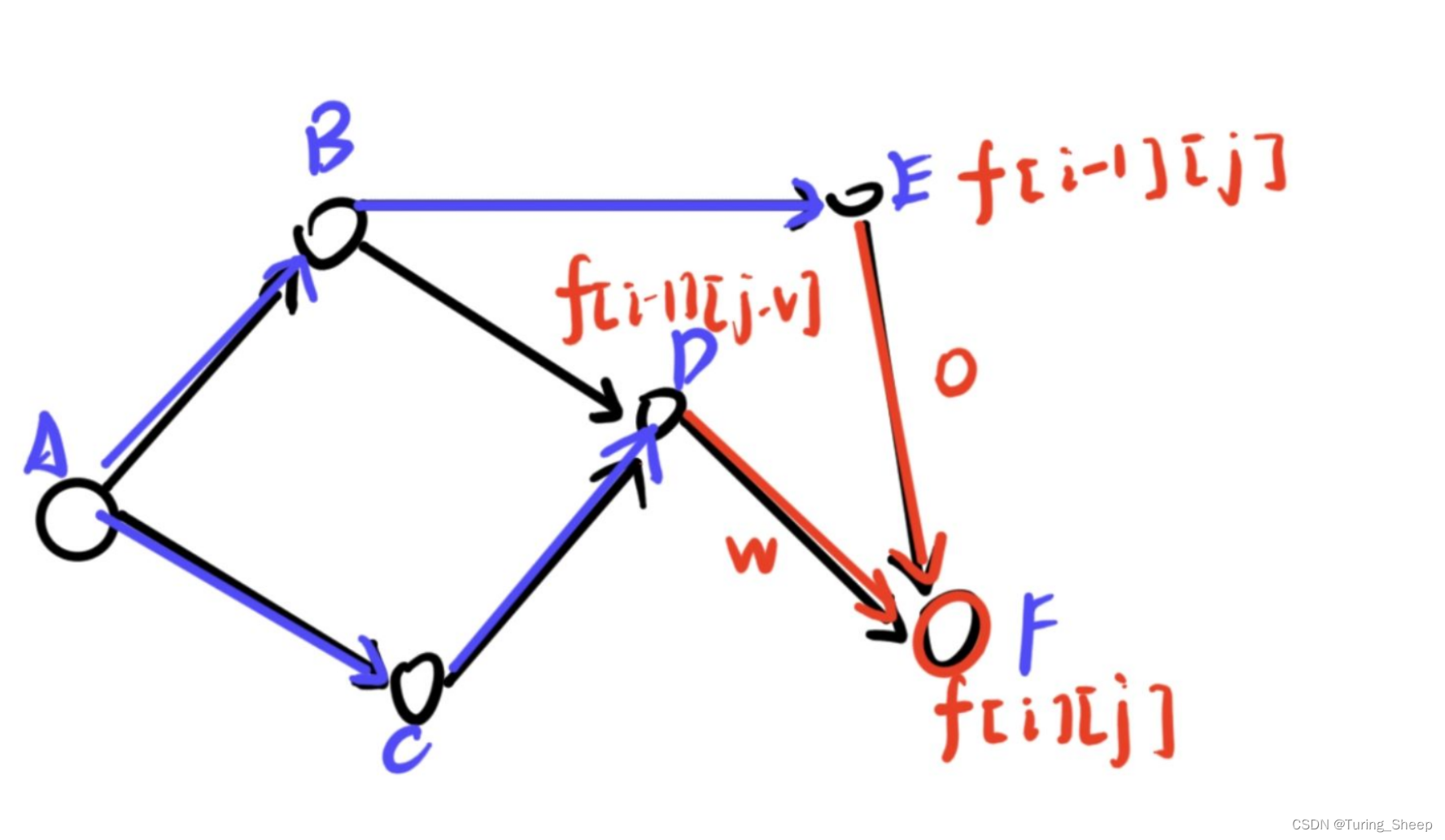
在这里插入图片描述
单纯地看这个图的话，还是比较抽象的，因此我们把01背包的方程映射到这个图中，（这里只是因为01背包比较容易映射，分组背包等问题同理）。我们发现想要得到F状态可以通过DF和EF两个状态通过边分别转移过来。但是我们想得到的是最优的，如果两个转移状态的过程是相等的，即f[i-1][j-v]+w==f[i-1][j]，那么就说明这两个边都可以（所以我们将这两个边搞成红色），任意选一个边即可。

接着，我们以DF这条边为例子，我们还需要知道D状态怎么转化而来，同理我们比较CD和BD两个转移过程，发现CD是最优的，那么DC就是最优解方案中的一部分。

就这样我们可以从终点逆推起点，从而记录方案。

那么这道题也同理，对于一个点而言，可以由前一个组内的任意一个物品转移过来，但是我们需要通过比较找到最优的路线。然后慢慢地逆推得到方案。

三、代码

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=15,M=20;
int f[N][M],v[N][M],w[N][M];
int way[N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        {
            scanf("%d",&w[i][j]);
            v[i][j]=j;
        }
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
            for(int k=0;k<=m;k++)
            {
                if(j>=v[i][k])
                f[i][j]=max(f[i][j],f[i-1][j-v[i][k]]+w[i][k]);
            }
        }
    }
    cout<<f[n][m]<<endl;
    int j=m;
    for(int i=n;i>=1;i--)
    {
        for(int k=0;k<=m;k++)
        {
            if(j>=v[i][k]&&f[i][j]==f[i-1][j-v[i][k]]+w[i][k])
            {
                way[i]=k;
                j-=k;
                break;
            }
        }
    }
    for(int i=1;i<=n;i++)cout<<i<<" "<<way[i]<<endl;   
    return 0;
}