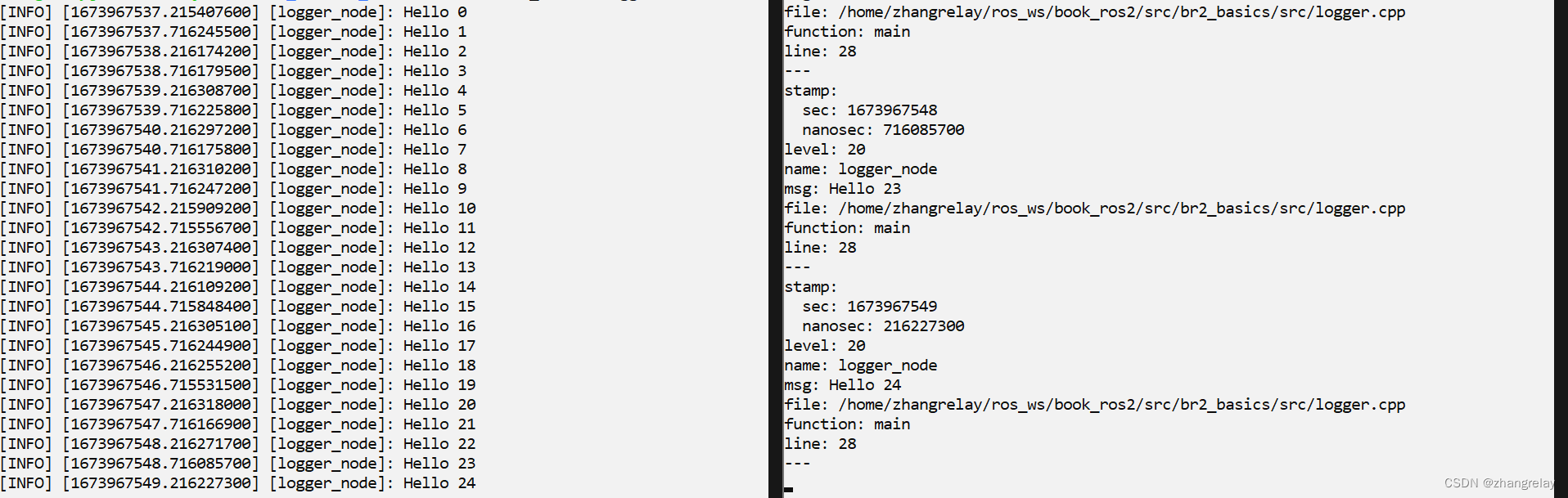
(1)位运算的本质,其实是对二进制补码储存形式的修改。
位运算常见的运算符为
<<左移n个位置(算数移位,符号位不变)
>>右移动n个位置(采用直接丢弃末尾数字的方法,符号位不变)
(移位都是算数移位)
~按位取反(对于包括符号位在内全部取反)
&按位与
|按位或
^按位异或
注意上述操作,全是对补码进行的,所以说学好计算机组成很重要(2)位运算时候要注意的几个问题
(1)关于负数左移溢出,在实际应用里面遇到了这个问题
先说是怎么样移动的,比如100111(假设这种数据类型长度只有六位,补码)
左移移位就会变成001110,是个正数。但是右移的时候会变成110011,还是个负数。这种移动方法似乎和王道等课程的说法不同,下面两个实验验证并总结
cout<<((int)(pow(2,30))<<1)<<endl;
//这个东西其实就是0,100000000.。。000;左移一位变成最小负数1,0000000000...000
//这就印证了(存储和操作的形式是补码)(符号位参与移动/逻辑移位)
cout<<((-2)>>1);
//1,1111111..10 右移一位变成1,11111111.。11;
//转化为源码就是1,000000.。01,结果就是-1,这里可以看出符号位不参与移动
//或者说负数补码补的是1,所以等于没移动(可以视作算数移位)
//总结起来就是对于无符号数,右移为算术移位,左移为逻辑移位,只有向右才会涉及到符号的保留所以一般涉及到左右移位的时候,我们要尽可能使用无符号数来减少错误(unsigned int)
(2)因为是补码嘛,所以取反的结果可能不太一样。取反的时候连同符号位一起变化,并且是对补码形式进行操作。但是变成数值的时候还是按照补码转化源码的规则来的。
所以说尽量不要对负数进行取反操作
(3)遇到的几个题
(1)第一种类型,对于一个数的二进制形式进行判断
比如2的幂次方,结构就0001000..000,判断方法就是先按位取反1110111..111,然后和原本进行异或操作,如果异或结果为0,就代表符合这个结构
再比如4的幂次方,这个就不能用形式进行位操作的,要用数学归纳找到规律
//231题 2的幂
//原理为,(n)1000 (n-1)0111进行&操作,如果结果为0,那就是2的幂次方
//或者说相加为2n-1,也是可以的
//另外好要注意一个情况,2的n次方一定是正数
bool isPowerOfTwo(int n) {
if((n&(n-1))==0){
return true;
}else{
return false;
}
}
//342 4的幂
//4的幂的特点就是,在2次幂次方的基础上,mod3=1
bool isPowerOfFour(int n) {
if((n>0&&n&(n-1))==0){
return (n%3==1);
}else{
return false;
}
}
191题,检查1的位数
//191,每次向右移动一位,然后和1进行&操作,每个位置都检查一遍
int hammingWeight(uint32_t n) {
int count=0;
for(int i=1;i<=32;i++){
if((n&1)==1)
count++;
n>>1;
}
return count;
}面试题16.01,两数交换,其实运用的离散数学的规则就是a=a^b^b;
//面试题目16.01,两数交换,不开辟别的变量,交换两个数字
//注意这两个数字可能查出int最大界限,所以不能移动到没有计数的位置上,而是用^的方法进行处理
//举个例子,a=1101 b=0110; 先a=a^b=1011;1代表这个位置上ab不一样,0代表了这个位置上数字一样的
//分析,接下来a=1011,b=0110,分为四种情况
//如果a是1,b也是1,那么就代表原本的a在这位上和b不一样,为0
//如果a是1,b也是0,那么就代表原本的a在这位上和b不一样,为1
//如果a是0,b也是1,那么就代表原本的a在这位上和b一样,为1
//如果a是0,b也是0,那么就代表原本的a在这位上和b一样,为0
//这个关系恰好为异或,也就是说存在一个a=a^b^b的关系
//所以b可以变化为a,a也可以直接转化为b
vector<int> swapNumbers(vector<int>& numbers) {
//原理其实就是a^b^b=a
numbers[0]=numbers[0]^numbers[1];
numbers[1]=numbers[0]^numbers[1];
numbers[0]=numbers[0]^numbers[1];
return numbers;
}136题,寻找数组里单个的数字。。。这个可以说是专门为异或准备的一个题了
//136题,寻找单个的数,用位运算就能解释
int singleNumber(vector<int>& nums) {
int n=0;
for(int i=0;i<nums.size();i++){
n=n^nums[i];
}
return n;
}693题,判断一个二进制数是否为交替的,这个题目还是蛮重要的。
思路就是两位两位地进行判断,采用右移(这题给的就是正整数,所以不用担心符号位是啥)
判断方法,和00000000..0011进行异或,如果结果为0或者11就代表这两位是一样的
//693交替二进制数
//写法上要注意点问题就是,有符号数的负值进行左移时会发生溢出报错,因为第一位符号位不变
//所以说尽可能右侧移动
bool hasAlternatingBits(int n) {
while(n){
if((n&3)!=0&&(n&3)!=3){
n=n>>1;
}else{
return false;
}
}
return true;
}371题。。你可能需要更多一点的经验才能很快地做出这道逆天题目

先分析一下这道题,明显是要用位运算了
比如两个数字 a=011,b=010;
相加的话,首先a^b=001,这是按位相加后每一位的数字,a&b结果为010,是每个位置上产生的进位,因为每个位的进位要加到更高位上,所以就可以转化为
0001+0100(a&b左移一位,再和a^b相加),一直往下,直到没有进位(a&b变成0了),就返回此时的啊a
所以说这题很容易就能用递归处理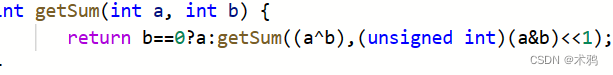
另外关于我们之前一直关心的负数问题,递归过程中根据异或和且的性质,可以保留的
面试题15.01,纯纯的位操作
把对应位置全都改成0,然后直接加上移动后的数字即可
//15.01面试题
//其实不要给自己下绊子来得更快
int insertBits(int N, int M, int i, int j) {
int n=pow(2,j-i+1)-1;//这个的计算没出问题
int u=(N&~(n<<i))+(M<<i);
return u;
}