BFS的入门与应用

news2024/12/31 7:05:14

目录

一、前言

二、BFS原理

二、BFS与最短路径

1、最短路径问题用BFS

2、迷宫（2019年省赛，填空题，lanqiaoOJ题号602）

（1）字典序最小的最短路径

（2）输出路径的两种方法

三、BFS与连通性判断

1、全球变暖（2018年省赛，lanqiaoOJ题号178）

（1）queue

（2）list

（3）deque

2、剪邮票（2016年省赛，填空题，lanqiaoOJ题号1505）

一、前言

本文主要讲了BFS的原理、BFS与最短路径、BFS与连通性判断以及相应的例题。

二、BFS原理

BFS搜索的原理：“逐层扩散”。从起点出发，按层次从近到远，逐层先后搜索。

编码：用队列实现。

应用：BFS 一般用于求最短路径问题，BFS 的特点是逐层搜索，先搜到的层离起点更近。

【比如：找从@到*的最短路径】

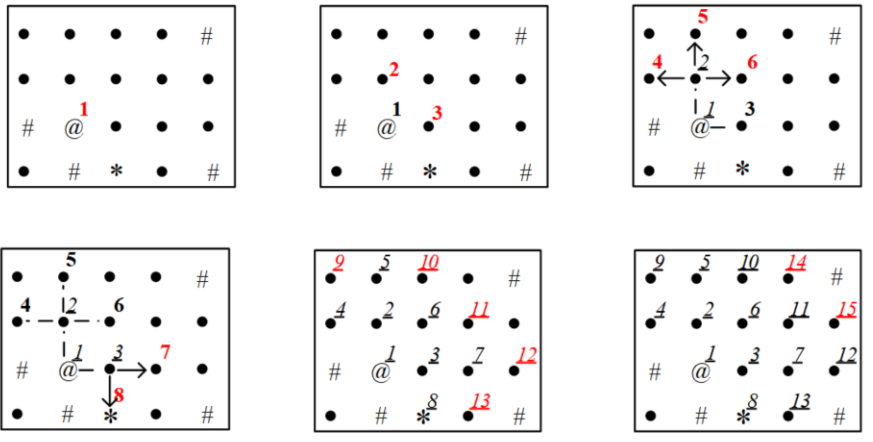
【用队列实现】

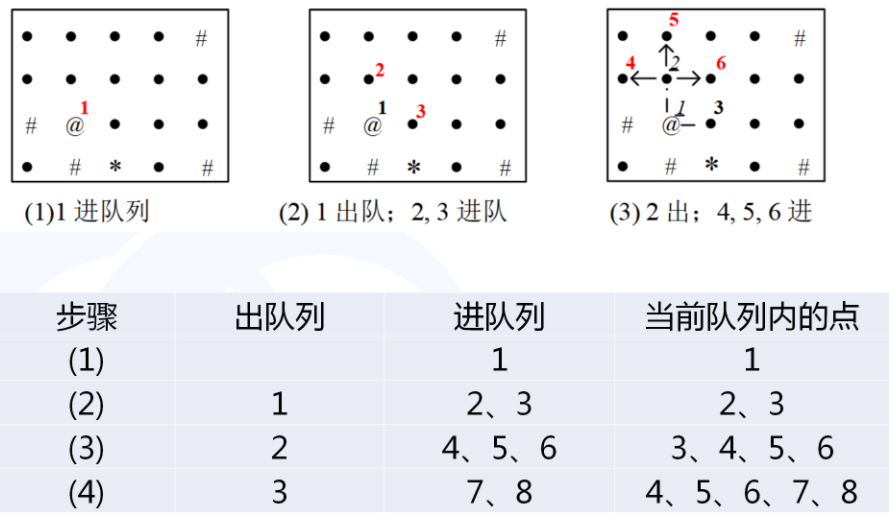
二、BFS与最短路径

1、最短路径问题用BFS

BFS的特点：逐层扩散。

  • 往 BFS 的队列中加入邻居结点时，按距离起点远近的顺序加入：先加入距离起点为 1 的邻居结点，加完之后，再加入距离为 2 的邻居结点，等等
  • 搜完一层，才会继续搜下一层。

最短路径：从起点开始，沿着每一层逐步往外走，每多一层，路径长度就增加 1。

所有长度相同的最短路径都是从相同的层次扩散出去的。

搜到第一个到达终点的路径，就是最短路径。

【应用场合】

点和点直接的距离是1，即边长是1。

2、迷宫（2019年省赛，填空题，lanqiaoOJ题号602）

【题目描述】

下图给出了一个迷宫的平面图，其中标记为 1 的为障碍，标记为 0 的为可以通行的地方。

010000

000100

001001

110000

迷宫的入口为左上角，出口为右下角，在迷宫中，只能从一个位置走到这个它的上、下、左、右四个方向之一。对于上面的迷宫，从入口开始，可以按 DRRURRDDDR 的顺序通过迷宫，一共 10 步。其中 D、U、L、R 分别表示向下、向上、向左、向右走。对于下面这个更复杂的迷宫 (30行50列)，请找出一种通过迷宫的方式，其使用的步数最少，在步数最少的前提下，请找出字典序最小的一个作为答案。请注意在字典序中 D<L<R<U。

（1）字典序最小的最短路径

  • 题目求字典序最小的最短路径
  • 在每次扩散下一层 (往 BFS 的队列中加入下一层的结点) 时，按字典序 "D<L<R<U" 的顺序加下一层的结点，那么第一个搜到的最短路径就是字典序最小的。
  • 计算复杂度：每个点只搜一次，即进入队列和出队列一次。复杂度 O(n)，n 是迷宫内结点的总数。
  • BFS 能用于解决1千万个点的最短路问题。

（2）输出路径的两种方法

【简单方法】

  • 每扩展到一个点 v，都在 v 上存储从起点 s 到 v 的完整路径。
  • 到达终点 t 时，得到了从起点 s 到 t 的完整路径。

优点：简单、适合小图。

缺点：占用大量空间，因为每个点上都存储了完整的路径。不适合大图。

from queue import Queue

mp=[]
for i in range(0,30):
    mp.append(input())      #读迷宫
for i in range(len(mp)):
    mp[i]='1'+mp[i]+'1'     #为迷宫加左边和右边的围墙
mp=[52*'1']+mp+[52*'1']     #为迷宫加上面和下面的围墙

#print([52*'1'])
#print(mp)                  mp现在是一个只含有字符串的列表

vis=[list(map(int,list(i))) for i in mp]    #记录迷宫的状态,vis是一个二维数组
#print(vis)

k=('D','L','R','U')         #方向
dir=((1,0),(0,-1),(0,1),(-1,0))

vis[1][1]=1         #起点是(1,1),终点是(30,50)
q=Queue()           #BFS: 队列实现
q.put((1,1,""))     #队列: 坐标x、坐标y、路径
while q.qsize()!=0: #以(1,1)为起点开始移动
    x,y,p=q.get()
    if x==30 and y==50:
        print(p)
        exit	    #打印完整路径，退出
    for i in range(4):
        nx=x+dir[i][0]
        ny=y+dir[i][1]
        if vis[nx][ny]!=1:  #把访问过的点变成墙，后面不再访问
            vis[nx][ny]=1
            path=p+k[i]     #记录从起点到这个点的完整路径
            q.put((nx,ny,path))

【标准方法】

  • 在每个点上记录它的前驱点
  • 从终点一步步回溯到起点，得到一条完整路径。

优点：节省空间，因为每个点上只存储了上一个点。适合大图。

(在DFS中，路径可以用栈来记录，参考 19 讲 “路径之谜，lanqiaoOJ题号89” )

from queue import Queue
def print_path(x,y):
    if x==1 and y==1:
        return          #回溯到了起点，递归结束，返回
    if pre[x][y]=='D':
        print_path(x-1,y)   #回溯，往上 U
    if pre[x][y]=='L':
        print_path(x,y+1)   #回溯，往右 R
    if pre[x][y]=='R':
        print_path(x,y-1)   #回溯，往左 L
    if pre[x][y]=='U':
        print_path(x+1,y)
    print(pre[x][y],end="")

mp=[]
for i in range(0,30):
    mp.append(input())      #读迷宫
for i in range(len(mp)):
    mp[i]='1'+mp[i]+'1'     #为迷宫加左边和右边的围墙
mp=[52*'1']+mp+[52*'1']     #为迷宫加上面和下面的围墙
vis=[list(map(int,list(i))) for i in mp]    #记录迷宫的状态
k=('D','L','R','U')     #方向
dir=((1,0),(0,-1),(0,1),(-1,0))

pre=[[(-1,-1)]*(52) for i in range(32)]     #用于保存前一个点
#下面是bfs
vis[1][1]=1     #起点是(1,1),经过了这一点，就把这一点变成围墙
q=Queue()
q.put((1,1))
while q.qsize()!=0:     #以(1,1)为起点开始移动
    x,y=q.get()
    if x==30 and y==50:
        print_path(30,50)
        exit            #打印路径，退出
    for i in range(4):      #BFS: 队列实现
        nx=x+dir[i][0]
        ny=y+dir[i][1]
        if vis[nx][ny]!=1:      #把访问过的点变成墙，后面不再访问
            vis[nx][ny]=1
            pre[nx][ny]=k[i]
            q.put((nx,ny))

三、BFS与连通性判断

连通性判断：

图论的一个简单问题，给定一张图，图由点和连接点的边组成，要求找到图中互相连通的部分。（在DFS中，我们也讲解了连通性判断）

1、全球变暖（2018年省赛，lanqiaoOJ题号178）

【题目描述】

你有一张某海域 NxN 像素的照片，"." 表示海洋、"#" 表示陆地，如下所示：

其中 "上下左右" 四个方向上连在一起的一片陆地组成一座岛屿。例如上图就有 2 座岛屿。由于全球变暖导致了海面上升，科学家预测未来几十年，岛屿边缘一个像素的范围会被海水淹没。具体来说如果一块陆地像素与海洋相邻 (上下左右四个相邻像素中有海洋)，它就会被淹没。例如上图中的海域未来会变成如下样子：

请你计算：照片中有多少岛屿会被完全淹没。照片保证第 1 行、第 1 列、第 N 行、第 N 列的像素都是海洋。

【输入描述】

第一行包含一个整数 N (1<N<1000)。以下 N 行 N 列代表一张海域照片。

【输出描述】

输出一个整数表示答案。

【BFS判断连通性的步骤】

  • 从图上任意一个点 u 开始遍历，把它放进队列中。
  • 弹出队首 u，标记 u 已搜过，然后搜索 u 的邻居点，即与 u 连通的点，放到队列中。
  • 继续弹出队首，标记搜过，然后搜索与它连通的邻居点，放进队列。

继续以上步骤，直到队列为空，此时一个连通块已经找到。

其他没有访问到的点，属于另外的连通块，按以上步骤再次处理这些点。

最后所有点都搜到，所有连通块也都找到。

【什么岛屿不会被完全淹没】

  • 若岛中有个陆地（称为高地），它周围都是陆地，那么这个岛不会被完全淹没。
  • 用 BFS 搜出有多少个岛（连通块），检查这个岛有没有高地，统计那些没有高地的岛 (连通块) 的数量，就是答案。
  • 计算复杂度：每个像素点只用搜一次且必须至少搜一次，共 N^2 个点，BFS 的复杂度是 O(N^2)，不可能更好了。

【BFS的三种实现】

  • queue
  • list
  • deque。 deque最快

用 “全球变暖” 这题演示三种实现

（1）queue

from queue import *
def bfs(x,y):
    global flag
    q=Queue()
    q.put((x,y))
    vis[x][y]=1
    while not q.empty():
        x,y=q.get()
        if mp[x][y+1]=='#' and mp[x][y-1]=='#' and mp[x+1][y]=='#' and mp[x-1][y]=='#':
            flag=1
        for u,v in ((0,1),(0,-1),(1,0),(-1,0)):     #拓展四个方向
            nx=x+u
            ny=y+v
            if vis[nx][ny]==0 and mp[nx][ny]=="#":
                q.put((nx,ny))
                vis[nx][ny]=1

n=int(input())
mp=[]
for i in range(n):
    mp.append(list(input()))
vis=[]
for i in range(n):
    vis.append([0]*n)
ans=0
for i in range(n):
    for j in range(n):
        if vis[i][j]==0 and mp[i][j]=="#":   #没被访问过且是陆地
            flag=0
            bfs(i,j)
            if flag==0:
                ans+=1
print(ans)

（2）list

def bfs(x,y):
    global flag
    q=[(x,y)]   #用list实现队列
    vis[x][y]=1
    while q:
        x,y=q.pop(0)
        if mp[x][y+1]=='#' and mp[x][y-1]=='#' and mp[x+1][y]=='#' and mp[x-1][y]=='#':
            flag=1
        for u,v in ((0,1),(0,-1),(1,0),(-1,0)):     #拓展四个方向
            nx=x+u
            ny=y+v
            if vis[nx][ny]==0 and mp[nx][ny]=="#":
                q.append((nx,ny))
                vis[nx][ny]=1

n=int(input())
mp=[]
for i in range(n):
    mp.append(list(input()))
vis=[]
for i in range(n):
    vis.append([0]*n)
ans=0
for i in range(n):
    for j in range(n):
        if vis[i][j]==0 and mp[i][j]=="#":   #没被访问过且是陆地
            flag=0
            bfs(i,j)
            if flag==0:
                ans+=1
print(ans)

（3）deque

deque 最快，建议需要用队列时，用 deque

from collections import *
def bfs(x,y):
    global flag
    q=deque()
    q.append((x,y))
    vis[x][y]=1
    while q:
        x,y=q.popleft()
        if mp[x][y+1]=='#' and mp[x][y-1]=='#' and mp[x+1][y]=='#' and mp[x-1][y]=='#':
            flag=1
        for u,v in ((0,1),(0,-1),(1,0),(-1,0)):     #拓展四个方向
            nx=x+u
            ny=y+v
            if vis[nx][ny]==0 and mp[nx][ny]=="#":
                q.append((nx,ny))
                vis[nx][ny]=1

n=int(input())
mp=[]
for i in range(n):
    mp.append(list(input()))
vis=[]
for i in range(n):
    vis.append([0]*n)
ans=0
for i in range(n):
    for j in range(n):
        if vis[i][j]==0 and mp[i][j]=="#":   #没被访问过且是陆地
            flag=0
            bfs(i,j)
            if flag==0:
                ans+=1
print(ans)

2、剪邮票（2016年省赛，填空题，lanqiaoOJ题号1505）

【题目描述】

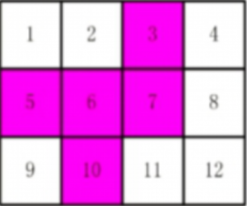
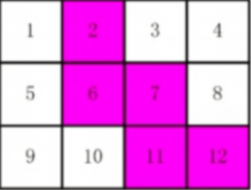
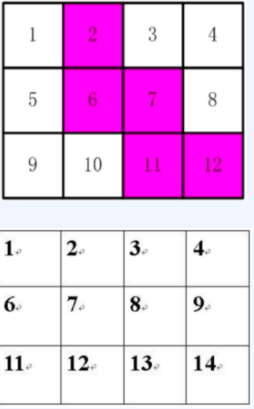
有 12 张连在一起的 12 生肖的邮票。现在要从中剪下 5 张来，要求必须是连着的。仅仅连接一个角不算相连。比如图中，粉红色所示部分是合格的剪取。

请你计算一共有多少种不同的剪取方法。

 

【思路：暴力求全排列+检查连通性】

（1）用递归暴力列出所有可能的排列：从 12 个数中选 5 个数进行全排列。

（2）判断这 5 个数是否连通。

算法复杂度：12*11*10*9*8=12!/7!=95040

可行！

【判断 2 个数是否连通】

小技巧：

  • 在原图中向上为 -4，向下为 +4，向左为 -1，向右为 +1，但是遇到 34578 这种 4+1=5，这种情况不符合，所以重构一下原图。
  • 向上为 -5，向下为 +5，向左为 -1，向右为 +1。

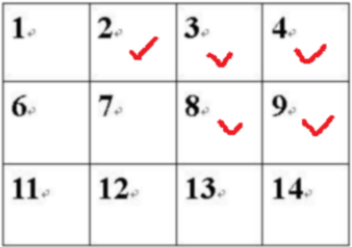
判断图中的 {2，3，4，8，9} 是否连通。用队列：

  • 2 进队列：当前队列是(2)；
  • 2 的邻居进(push)队列：当前队列是(2 3);
  • 弹出(pop)2：当前队列是(3);
  • 3 的邻居进队列：当前队列是(3 4 8);
  • 弹出 3；当前队列是(4 8)
  • 4 的邻居进队列：当前队列是(4 8 9)
  • 弹出 4：当前队列是(8 9)
  • 8没有没处理过的邻居了。
  • 弹出 8：当前队列是(9)
  • 弹出9;
  • 队列空。

如果5个数都进过队列，它们就是连通的。

from queue import *
def bfs():      #a[0]~a[4]这前5个数是递归出来的5个数。用BFS判断它们是否连通
    vis=[0]*5   #这5个数的状态，判断其中某个数是否已经用队列处理过
    p=0         #进队列的个数。如果5个数都进过队列，说明这5个数连通
    q=Queue()
    q.put(0)    #第一个进队列的数
    vis[0]=1    #表示0用队列处理过了
    while not q.empty():
        i=q.get()   #得到队列的第一个数
        p+=1
        for j in range(5):
            if vis[j]==0:   #j没有用队列处理过
                for k in (-1,1,-5,5):   #k是上下左右4个方向
                    if a[i]+k==a[j]:    #与j在k方向连接
                        q.put(j)
                        vis[j]=1        #进队列了
    if p==5:
        return True
    else:
        return False

def perm(s,t):
    global num
    if s==5:
        if bfs()==True:
            num+=1          #得到一个5个数的排列，用bfs判断5个数是否连通
    else:
        for i in range(s,t+1):
            a[s],a[i]=a[i],a[s]     #交换
            perm(s+1,t)
            a[i],a[s]=a[s],a[i]

a=[1,2,3,4,6,7,8,9,11,12,13,14]     #不包括5, 10
num=0           #统计排列数
perm(0,11)      #求从第0个数到第11个数的全排列
print(num//120) #除以120得到组合数

以上，BFS的入门与应用

祝好

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/170678.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

拉伯证券|今年首批游戏版号发放，机构看好春节行业景气度恢复

拉伯证券|今年首批游戏版号发放，机构看好春节行业景气度恢复

2023年第一批游戏版号发放。 昨日晚间&#xff0c;国家新闻出版署发布1月国产网络游戏审批信息&#xff0c;共88款游戏获批&#xff0c;其我国内各大游戏龙头均有所收成&#xff0c;包含腾讯《黎明觉悟&#xff1a;活力》、网易《逆水寒》&#xff08;移动版&#xff09;、完美…
阅读更多...
数据治理：数据治理之道-组织机制-敏捷的治理组织

数据治理：数据治理之道-组织机制-敏捷的治理组织

参考《一本书讲透数据治理》、《数据治理》等 组织机制&#xff1a;敏捷的治理组织 数据、组织、软件平台&#xff0c;是企业数字化转型面临的三座大山 数据&#xff1a;数据是企业数字化转型的根本驱动力之一&#xff0c;数字化转型中的企业必须做好数据治理与应用&#xff…
阅读更多...
8Manage：分散的软件正在扼杀公司的生产力

8Manage：分散的软件正在扼杀公司的生产力

在企业领域&#xff0c;数字化不仅仅是指工具能力&#xff0c;而是指用户如何很好地应用他们的知识来做决策&#xff0c;培养关系&#xff0c;建立声誉&#xff0c;以及动员同事、团队。几十年来&#xff0c;企业已经部署了生产力、搜索和协作平台&#xff0c;以提高员工和业务…
阅读更多...
使用 tslib 库

使用 tslib 库

tslib 是专门为触摸屏设备所开发的 Linux 应用层函数库&#xff0c;并且是开源。tslib 为触摸屏驱动和应用层之间的适配层&#xff0c; 它把应用程序中读取触摸屏 struct input_event 类型数据&#xff08;这是输入设备上报给应用层的原始数据&#xff09;并进行解析的操作过程…
阅读更多...
ceres学习笔记(三)

ceres学习笔记(三)

学习了example中pose_graph_3d的部分&#xff0c;记录一下学习过程。 前言&#xff1a; 翻译一下readme里面的内容&#xff1a; ... 该示例还说明了如何将 Eigen 的几何模块与 Ceres 的自动微分功能结合使用。 为了表示方向&#xff0c;我们将使用 Eigen 的四元数&#xff…
阅读更多...
测试开发 | Pytest 结合 Allure 生成测试报告

测试开发 | Pytest 结合 Allure 生成测试报告

本文节选自霍格沃玆测试学院测试开发内部教材&#xff0c;进阶学习文末加群&#xff01; 测试报告在项目中是至关重要的角色&#xff0c;一个好的测试报告&#xff1a; 可以体现测试人员的工作量&#xff1b; 开发人员可以从测试报告中了解缺陷的情况&#xff1b; 测试经理可…
阅读更多...
锂电产业如何利用视觉检测系统降本增效？

锂电产业如何利用视觉检测系统降本增效？

导语&#xff1a;机器视觉检测已在锂电池生产的各个环节中&#xff0c;为产品产量与质量提供可靠保障。维视智造作为锂电池视觉检测系统提供商&#xff0c;为企业提供专业、系统、稳定的锂电行业解决方案&#xff0c;可保证0漏检&#xff0c;确保安全生产&#xff0c;全面提升生…
阅读更多...
炫酷 RGB 之.NET nanoFramework 点灯大师

炫酷 RGB 之.NET nanoFramework 点灯大师

前面介绍了 .NET nanoFramework 入门&#xff0c;本文继续以微雪的 ESP32-S2-Pico 为例介绍 .NET nanoFramework 的开发&#xff1a;控制 ESP32 板载 RGB 灯 和 外接 RGB 灯。内容包含 状态灯的意义、WS2812 、HSV、PWM 等相关知识。 文章目录1. 背景2. 状态灯的意义3. 板载 LE…
阅读更多...
萌新如何使用printf函数？

萌新如何使用printf函数？

&#x1f40e;作者的话 如果你搜索输入输出函数&#xff0c;那么你会看到输入输出流、Turbo标准库、标准输出端、stdout什么什么乱七八糟的&#xff0c;作为一个萌新&#xff0c;哪懂这些&#xff1f; 本文介绍萌新在前期的学习中&#xff0c;常用的输入输出函数及其功能~ 跳跃…
阅读更多...
ROS2机器人编程简述humble-第二章-Controlling the Iterative Execution .3.1

ROS2机器人编程简述humble-第二章-Controlling the Iterative Execution .3.1

2.3 ANALYZING THE BR2 BASICS PACKAGE 这一节内容有些多……前一篇&#xff1a;ROS2机器人编程简述humble-第二章-DEVELOPING THE FIRST NODE .2里面只有节点&#xff0c;没有任何实际功能。logger.cpp代码如下所示&#xff1a;#include "rclcpp/rclcpp.hpp"using n…
阅读更多...
微信小程序分享的图片被裁切了。怎么让他不裁剪正常比例5:4显示

微信小程序分享的图片被裁切了。怎么让他不裁剪正常比例5:4显示

现在的效果 希望的效果 最主要的是下面的这个函数。把图片转成了5:4的临时图片 cutShareImg(doctorImg:string ){let thatthis;return new Promise((resolve) > {wx.getImageInfo({src: doctorImg, // 这里填写网络图片路径 success: (res) > {var data resconsole.l…
阅读更多...
使用 LibreOffice 将 word 转化为 pdf 并解决中文乱码问题

使用 LibreOffice 将 word 转化为 pdf 并解决中文乱码问题

目录 一、安装 LibreOffice 二、解决乱码问题 2.1 查看是否安装中文字体 2.2 准备字体 2.3 导入字体 2.4 验证 项目中有一个在线上传 word 并预览 pdf 报告的需求&#xff0c;因为项目部署在 ubuntu 上面&#xff0c;所以借助libreoffice 实现 word 转 pdf&#xff0c;然…
阅读更多...
详细实例说明+典型案例实现 对枚举法进行全面分析 | C++

详细实例说明+典型案例实现 对枚举法进行全面分析 | C++

第五章 枚举法 目录 ●第五章 枚举法 ●前言 1.简要介绍 2.代码及结果示例&#xff08;简单理解&#xff09; 3.生活实例 ●二、枚举法的典型案例——鸡兔同笼&质数求解 1.鸡兔同笼 2.质数求解&#xff08;枚举法&#xff09; ●总结 前言 简单的来说…
阅读更多...
最新 vue-cli 构建项目

最新 vue-cli 构建项目

vue-cli 构建项目 当前使用最新版本构建一个vue node项目 插件 vue-clivueelement-plusroutervuex 安装vue-cli npm install -g vue-cli安装完后 vue --version 查看版本 vue --version创建一个项目 vue create demo这里要选择版本&#xff0c;不同版本要相组合配置的插件…
阅读更多...
反射的基本使用

反射的基本使用

文章目录1. 一个需求引出反射2. 反射机制2.1 Java Reflection2.2 Java 反射机制可以完成2.3 反射相关的主要类2.4 反射优点和缺点2.5 反射调用优化-关闭访问检查3. Class类3.1 基本介绍3.2 Class类的常用方法3.3 获取Class类对象3.4 哪些类型有Class对象3.5 类加载3.6 类加载流…
阅读更多...
aws imagebuilder 理解并使用imagebuilder构建pcluster自定义ami

aws imagebuilder 理解并使用imagebuilder构建pcluster自定义ami

参考资料 ec2-image-builder-workshop Troubleshoot EC2 Image Builder 理解imagebuilder imagebuilder 使用 cinc-client 进行客户端统一配置&#xff0c;CINC is not Chef&#xff0c;而是chef的免费分发版本。 https://cinc.sh/about/ imagebuilder管道的整体逻辑如下 核…
阅读更多...
OpenHarmony如何切换横竖屏？

OpenHarmony如何切换横竖屏？

前言在日常开发中&#xff0c;大多APP可能根据实际情况直接将APP的界面方向固定&#xff0c;或竖屏或横屏。但在使用过程中&#xff0c;我们还是会遇到横竖屏切换的功能需求&#xff0c;可能是通过物理重力感应触发&#xff0c;也有可能是用户手动触发。所以本文主要带大家了解…
阅读更多...
Git 代码版本管理工具详解 进厂必备

Git 代码版本管理工具详解 进厂必备

目录前言Git 概述什么是版本控制&#xff1f;为什么需要版本控制&#xff1f;版本控制工具集中式分布式Git 工作机制Git安装Git 常用命令(部分)初始化本地库设置用户签名初始化本地库查看本地库状态***工作区代码编写***添加暂存区撤销工作区的修改***提交本地库***工作区修改代…
阅读更多...
选择排序算法的实现和优化

选择排序算法的实现和优化

初识选择排序&#xff1a; 算法思想[以升序为例]&#xff1a; 第一趟选择排序时&#xff0c;从第一个记录开始&#xff0c;通过n-1次关键字的比较&#xff0c;从第n个记录中选出关键字最小的记录&#xff0c;并和第一个记录进行交换 第二趟选择排序时&#xff0c;从第二个记…
阅读更多...
Linux学习笔记【part1】目录结构与VIM文本编辑器

Linux学习笔记【part1】目录结构与VIM文本编辑器

Linux基础篇学习笔记 1.CentOS 7 64位安装 第一步&#xff0c;在软件选择中可以设置图形界面。 第二步&#xff0c;手动分区中设置挂载点&#xff0c;分别为引导分区、通用分区和交换区。 第三步&#xff0c;设置内核崩溃转储机制&#xff0c;这对服务器来说非常有用。 第四步…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023