最大子矩阵
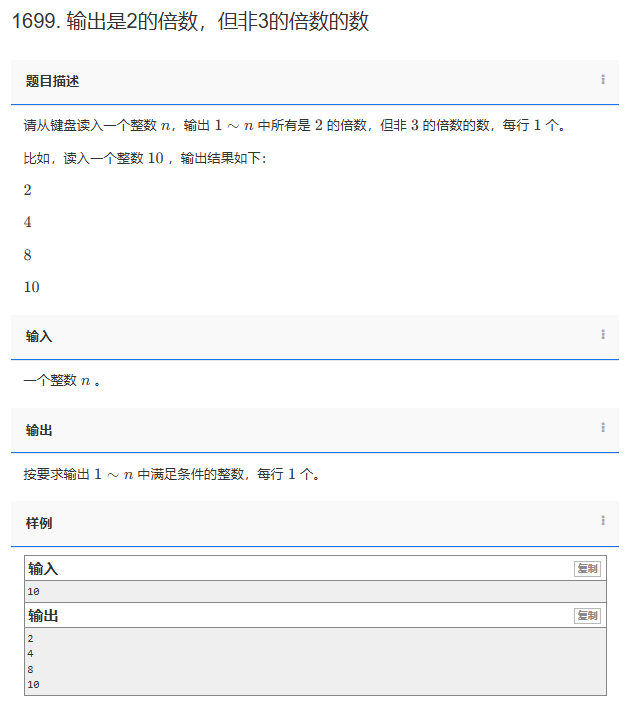
题目

思路
确定一个矩阵中的子矩阵,只需要确定矩阵对角线上两点的坐标即可,
在确定了子矩阵之后,还需要计算子矩阵中各元素之和,如果按照常规的循环方法来解决,时间复杂度是O(N^6),对于本题200长度大小,会超时,所以应该再另寻方法,仔细思考一番发现,确定子矩阵的四层循环,似乎是在所难免的,那么接下来的重点就是处理子矩阵中各元素和上边了,可以采用如下方法:定义一个同原始矩阵大小一样的矩阵,定义dp[i][j]为以[0][0]和[i][j]顶点矩阵的各元素之和,如果提前计算好,即将dp[][]的初始化和填表完成在寻找子矩阵之前,那么时间复杂度就变成了O(N^4),当确定好dp[][]之后,当确定了子矩阵的对角线上两点的坐标后,例如(x1,y1)和(x2,y2),将采取如下方法进行计算
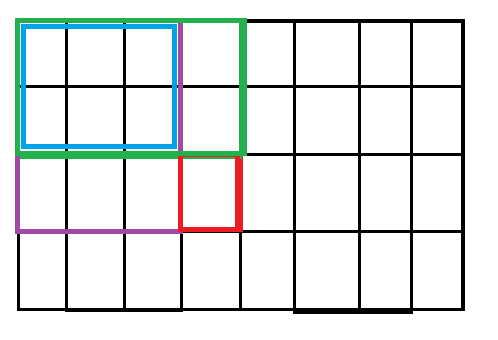
填写dp[][]表时,当填写红色位置的值时,只需将S(紫)+S(绿)-S(蓝)+红色位置在原始矩阵中对应的值即可,即dp[i][j]=dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]+matrix[i-1][j-1].(假设dp表比原始矩阵多一行,多一列)。
那么接下来在完成dp表的填写后,确定子矩阵的元素之和大小可采用如下方法:
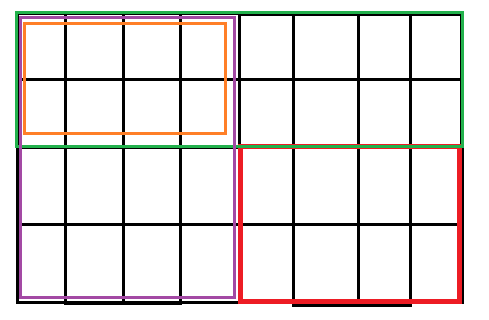
确定红色区域之和=整个区域-绿色区域-紫色区域+橙色区域
即S(红)= dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1].
在完成以上点之后,接下来确定最大子矩阵的坐标就信手拈来了,定义一个变量记录之前的最大值,当遇到破纪录的值时,更新最大子矩阵的坐标。
代码
class Solution {
public:
int dp[210][210];
vector<int> getMaxMatrix(vector<vector<int>>& matrix) {
vector<int> ans(4);
int a,b,c,d;
int m=matrix.size(),n=matrix[0].size();
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++)
dp[i][j]=dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]+matrix[i-1][j-1];
int ma=INT_MIN;
for(int x1=1;x1<=m;x1++)
for(int y1=1;y1<=n;y1++)
for(int x2=x1;x2<=m;x2++)
for(int y2=y1;y2<=n;y2++)
{
int ret=dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1];
if(ret>ma){
ma=ret;
// ans[0]=x1-1,ans[1]=y1-1,ans[2]=x2-1,ans[3]=y2-1;
a=x1-1,b=y1-1,c=x2-1,d=y2-1;
}
}
ans[0]=a,ans[1]=b,ans[2]=c,ans[3]=d;
return ans;
}
};经过试验发现,如果采用注释掉的方法进行更新,会超时,但是采用上边的方法,就可以通过了。
01矩阵
题目


思路
采用广度优先遍历来解决,创建一个同原始矩阵同样大小的矩阵dists,矩阵中各位置的值为该点距离0的最短距离,对于原始矩阵中值为0的点,在dists矩阵中对应的值为0,首先将原始矩阵中值为0的点放到队列中,然后不断地进行广度优先遍历,对于没遍历过的点,放入队列中,直到队列为空,更新结束。
代码
class Solution {
public:
vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
int m=mat.size(),n=mat[0].size();
vector<vector<int>> dists(m,vector<int>(n,INT_MAX));
queue<pair<int,int>> q;
for(int i=0;i<m;i++)
for(int j=0;j<n;j++)
{
if(mat[i][j]==0){
q.push({i,j});
dists[i][j]=0;
}
}
int dx[4]={0,0,1,-1};
int dy[4]={-1,1,0,0};
while(!q.empty()){
int a=q.front().first;
int b=q.front().second;
int dist=dists[a][b];
q.pop();
for(int k=0;k<4;k++){
int x=a+dx[k];
int y=b+dy[k];
if(x>=0 && x<m && y>=0 && y<n){
if(dists[x][y]>dist+1){
dists[x][y]=dist+1;
q.push({x,y});
}
}
}
}
return dists;
}
};