以太坊（2）——共识机制与挖矿算法

news2024/12/25 9:19:12

共识机制

ETH采用的是基于GHOST协议的共识机制

"GHOST"（Greedy Heaviest-Observed Sub-Tree）共识机制，它是以太坊使用的一种改进的区块链共识算法。GHOST共识机制旨在提高链的安全性和效率，通过考虑非主链区块的贡献，减少网络中的分支和拜占庭错误，从而增加整体网络的可靠性。

新的共识机制

原因

ETH的区块产生时间短，更容易出现分支

  1. 新的共识机制着力于解决挖出分支链该怎么办的问题

  2. 新的共识机制解决了 挖矿奖励与算力不成线性正比 和 使分支回到最长合法链 的两个问题

解决方法

对于挖出区块属于的非最长合法链的矿工予以补偿

为什么？

在ETH体系中，依旧有矿池的存在。假设按照BTC的处理方法

一个矿池挖出了一个区块，那么他肯定会沿着这个区块继续挖下去，而其他矿工的算力是分散的，而且更倾向于沿着矿池挖掘的最长合法链挖矿。这就导致了散户矿工拿到的收益与矿池拿到的收益和他们付出的算力不成正比，出现mining centralization的现象，矿池占到更大的便宜。

共识机制的演化

第一版

协议

  1. 每个区块可以包含uncle block，

  2. 被包含的uncle block获得出块奖励的7/8

  3. 包含uncle block的新区块额外获得出块奖励的1/32

  4. 对于uncle block，只判断它的哈希值是否合法，不管它的内容

优点

  1. 补偿了挖出分支区块的矿工

  2. 使得区块链分叉后的更快合并

存在问题

  1. 有的矿工去到很早的节点（几千几万个之前）挖分支区块，由于那时候挖矿难度低，他能获得大量区块，这时候他在主链上把这些区块当成uncle block包含进去，获得大量的以太币。

  2. 某些矿池为了压倒对手，故意不承认uncle block。损己一分，伤敌28倍

第二版

协议改进

  1. 规定uncle block获得的奖励为1-n/8。七代以内有共同祖先的区块才能算是uncle block

  2. 每个区块最多可以包含两个uncle block

改进意义

  1. 鼓励矿工尽早解决分支问题

  2. 小矿工可以尽早转入最长合法链，将自己的区块认作uncle block

区块实例

e0719ec2acb148189034cc3e8e2c9756.png

共识机制补充

局限

共识机制无法改变之前讲到的state fork（软/硬分叉）

BTC和ETH的收入

BTC

静态收入：挖矿奖励

动态收入：交易手续费

静态收入逐渐降低，是为了营造比特币“数字黄金”的稀缺性

ETH

静态收入：挖出最长合法链区块奖励 挖出分支区块的补偿 认叔奖励

动态收入：gas

静态收入基本不会降低，保证了gas费不会成为主要收入，进而保证了对于矿工的补偿机制，可以理解为，以太币是汽油（不会消失的消耗品）

另类uncle block

对于一个长分支链，每个区块都不会获得分支奖励

因为如果奖励的话会降低分叉攻击的成本。

挖矿算法

BTC挖矿的问题

挖矿设备的专业化，降低了去中心化的程度

one CPU，one Vote

因此，此后的加密货币要实现的是ASIC resistance

ASIC resistance可以先看一下BTC部分的挖矿

解决方案

  1. 内存，使得挖矿设备更接近通用计算机

  2. 权益证明，盘外招？

  3. 预挖矿，使得开发者拥有大量资产

方案一

设计需要大量内存的mining puzzle

这种mining puzzle的设计参考了莱特币

LiteCoin（莱特币）

  1. LiteCoin使用的是 scrypt mining puzzle

  2. scrypt mining puzzle是一种需要大量内存的哈希算法

  3. 设计原理：

    1. 创建一个数组，使用一个seed，计算出的值填在第一个位置

    2. 之后，第一个位置的数取哈希，放在第二个的位置，以此类推往后放，直到将整个数组填充满

    3. 在求解mining_puzzle的时候，先取出一个指定位置的存储结果，将这个结果进行一定的运算得到下一个位置；取出”下一个位置“的值，按上述的方法以此类推，最终得到结果

  4. 这样做的好处：使得求解过程变成memory_hord，如果你不用这个数组，计算难度就会大幅度上升（不存储，只能一次一次算到该位置的哈希）；如果你使用的话，对内存要求就会很高，实现了ASIC_resistance

  5. ASIC_resistance设计的核心思想是：增加计算过程对于内存的访问次数，使得这个过程跟贴近于普通计算机对于计算资源的配备

  6. 方案劣势：对于轻节点而言，也是memory_hard,因此在实际LiteCoin的使用中，最大的数组为128K。这也使得它对于ASIC的抵制性不高

ETH的挖矿设计

ETH挖矿使用了两个数据集小的是16M的 cache，大的是1G的dataset（DAG）

轻节点只用保存cache，矿工需要保存DAG

数据集

两个数据集的内存大小都在随时间上涨，适应计算机与日俱增的内存容量

cache

生成方式与莱特币数组生成的方式类似（seed在cache中）

DAG

  1. 根据cache，取出某个位置的数据，按照莱特币的方法，迭代256次，放入DAG数组的第一个位置，之后以同样的方法放在DAG的第二个位置，以此类推形成完整的DAG数据集

  2. 求解mining_puzzle的方法是，依照nonce和BlockHeader的数据，映射到DAG的某一个位置；取出这个位置和相邻下一个位置的数据，计算哈希映射到之后的位置，以此类推循环64次计算出区块哈希

  3. 验证区块哈希是否符合target要求

实现代码

ETHASH伪代码

生成cache

def mkcache(cache_size, seed):
    o = [hash(seed)]
    for i in range(1, cache_size):
        o.append(hash(o[-1]))
    return o

  1. 这个函数是通过seed计算出来cache的伪代码(cache中每个元素都是64字节的hash值)。

  2. 伪代码略去了原来代码中对cache元素进一步的处理，只展示原理，即cache中元素按序生成，每个元素产生时与上一个元素相关。

  3. 每隔30000个块会重新生成seed(对原来的seed求哈希值)，并且利用新的seed生成新的cache。

  4. cache的初始大小为16M，每隔30000个块重新生成时增大初始大小的1/128(128K)。

生成DAG

//生成DAG中的一个元素
def calc_dataset_item(cache, i):
    cache_size = cache.size
    mix = hash(cache[i % cache_size] ^ i)
    for j in range(256):
    cache_index = get_int_from_item(mix)
    mix = make_item(mix, cache[cache_index % cache_size])
return hash(mix)
//多次调用生成整个DAG
def calc_dataset(full_size, cache):
    return [calc_dataset_item(cache, i)for i in range(full_size)]

  1. 这是通过cache来生成dataset中第 i 个元素的伪代码。

  2. 这个dataset叫作DAG,初始大小为1G，每30000个块更新，同时增大初始大小的1/128（8M）

  3. 先通过cache中的第i%cache_size个元素生成初始的mix，因为两个不同的dataset元素可能对应同一个cache中的元素，为了保证每个初始的mix都不同，(i也参与哈希计算)

  4. 随后循环256次，每次通过get_int_from_item来根据当前的mix值求得一个要访问的cache元素的下标，用这个cache元素和mix通过make_ item求得新的mix值。(由于初始的mix值都不同，所以访问cache的序列也都是不同的)

  5. 迭代256次最终返回mix的哈希值，得到第 i 个dataset中的元素。

  6. 多次调用这个函数，就可以得到完整的dataset。

挖矿与验证

//全节点挖矿
挖出一次hash（取名为最终哈希）
def hashimoto_full(header, nonce, full_size, dataset):
    mix = hash(header, nonce)
    for i in range(64):
        dataset_index= get_int_from_item(mix) % full_size
        mix = make_item(mix,dataset[dataset index])
        mix = make_item(mix,dataset[dataset index + 1])
    return hash(mix)
挖出hash的主循环函数
def mine(full size, dataset, header,target):
    nonce =random.randint(0，2**64)
    while hashimoto_full(header, nonce, full_size, dataset)target:
        nonce =(nonce +1)%2**64
    return nonce
//轻节点验证
def hashimoto_light(header, nonce, full_size, cache):
    mix = hash(header.nonce)
    for i in range(64):
        dataset_index = get_int_from_item(mix) % full_size
        mix = make_item(mix, calc_dataset_item(cache, dataset index))
        mix = make_item(mix, calc_dataset_item(cache, dataset index + 1))
    return hash(mix)

挖矿一次函数

  1. 使用块头，使得轻节点存储占据内存小，方便验证。full_size是数据集的全部元素个数

  2. 首先根据块头的信息和nonce算出初始的哈希值。经过64次循环，每次循环读取大数据集中两个相邻的数（读取的位置由当前哈希值计算出），最后返回一个哈希值

挖出hash主循环函数

将调用一次上面挖矿函数返回的“最终哈希”与target进行比较，如果不满足，再调用挖矿函数

验证函数

  1. 这里的nonce是发布的区块块头里的nonce；使用cache验证，但是这里的full_size指的还是DAG里面的元素个数。

  2. 由于轻节点没有存储DAG，因此需要从cache中重新生成，其他操作的和上述生成一次最终hash类似

  3. 验证的操作分成两步，我们和BTC类比

    1. 验证哈希来源是否合法：BTC验证nonce值是不是生成hash的值，只需要结合块头进行一次哈希计算；而ETH的验证就是走一遍上面生成“最终哈希”的过程，看看生成的hash是不是公布的hash。

    2. 验证哈希是否符合要求（区块是否合法）：二者都验证了公布的hash是不是满足target要求

效果

对于轻节点而言，验证的时候只用进行一次“最终哈希的计算”，因此可以逐次计算1G的DAG，但是对于矿工而言。如果存储DAG，每次试“最终哈希”的时候都可以使用，如果不存储，每次都要算，计算量大大提升。

实际上，ETH使用的挖矿算法ethash，到目前为止有效的将挖矿手段限制在了GPU的水平，取得了很好的ASIC_resistance的效果

方案二

使用权益证明（PoS）替代工作量证明（Pow）

权益证明

在权益证明中，区块的产生不再依赖于计算复杂的数学题，而是通过持有和抵押一定数量的以太币（ETH）来获得网络的投票权。持有更多以太币的节点将有更高的几率被选为下一个出块节点，并且会因此获得相应的奖励。

吓唬大家的手段？

之后会讲

方案三

预挖矿（Pre-mining）：发行的一部分货币留给以太坊的开发者

预售（Pre-sale）：将一部分Pre-mining货币换成资产（现实），用于以太坊的开发工作。如果投资者看好这种货币，可以在Pre-sale阶段购买，等到货币成熟（升值）之后获得收益。

4a136fb924eb46d5a61b20430d96f52c.png

挖矿挖的再努力，赢在起跑线上最重要！（dog）

关于安全性的另一种想法

使用ASIC挖矿有利于安全性提高

  1. 增加了攻击的代价ASIC芯片具有专一性，研发周期长，研发投入高的特点。因此，购买大量矿机的矿池，拥有大量的该货币资产。他们会尽量维持区块链的安全性，因为如果安全性降低（被攻击），该货币就会贬值。

    1. 挖矿收入和现有资产缩水

    2. 购入的矿机由于只能挖这一条链，所以现有的矿机化为废品

  2. 如果通用计算机可以挖矿，那么一些不法分子可能通过租借云计算资源的方式进行攻击，攻击的硬件成本大大降低，区块链安全性下降

至于哪种说法对？具体情况具体分析

挖矿难度的调整

调整算法

基础调整

492704647fc54246be93ca2ec936eb5c.png

  1. 难度炸弹是为了向权益证明过渡

  2. 红色部分设置的是挖矿的难度下限

36cbdd8da8974da79b398b76edd3d984.png

ea75fef64dd14345a1d8a6cd827d6908.png

难度炸弹

c272722298334d29a59b6fe2dc74ab24.png

由于权益证明会导致现有的ETH挖矿体系的硬件设备报废，为了防止出现节点因为不同的意见（造成社区的分裂）而出现分叉的情况，设计了难度炸弹。

之前是设置难度炸弹逼大家转，后来是PoS设计不出来，不得不延长“爆炸”的时间，将区块号回退3000000个。

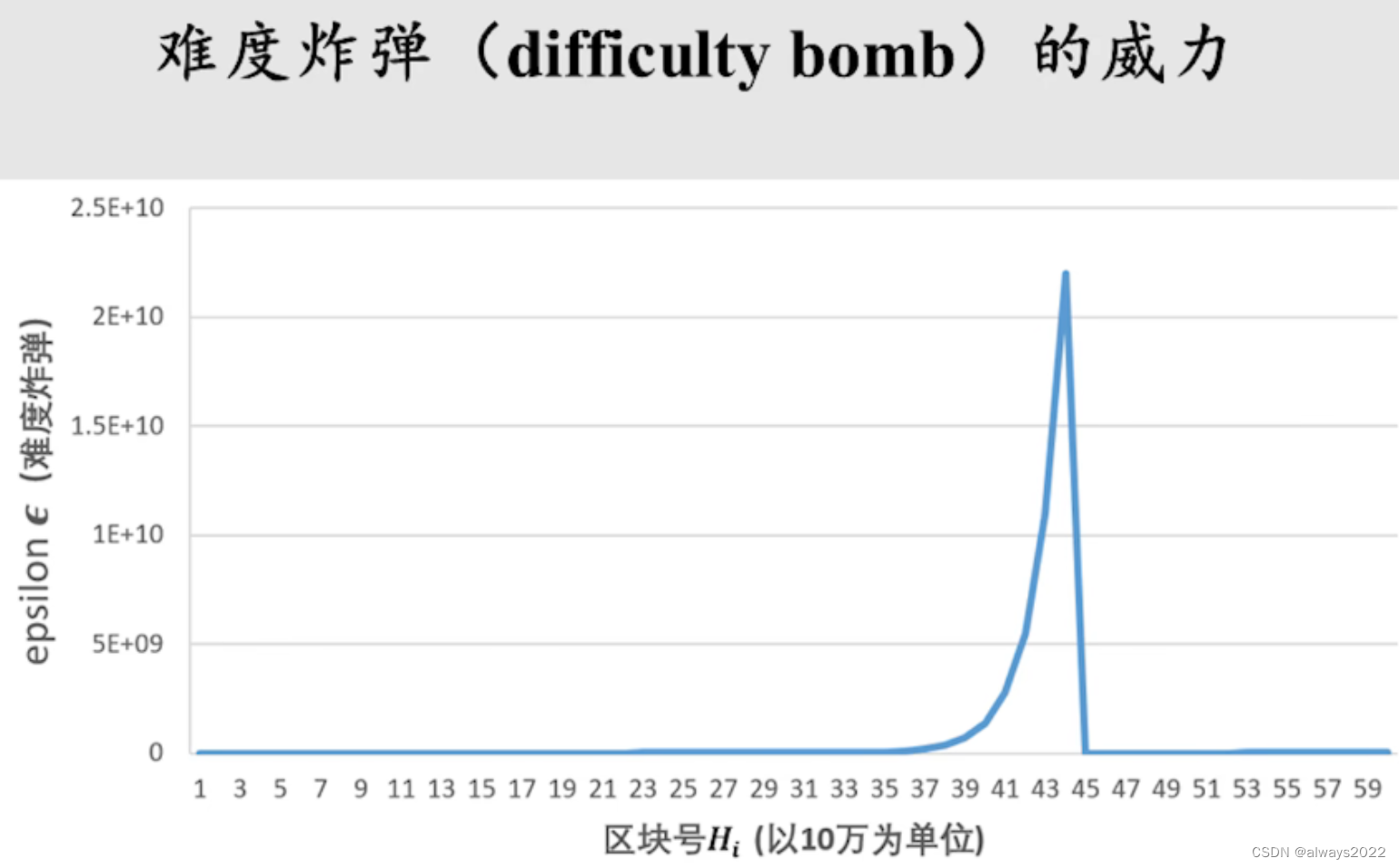
c6163386061b42b2afba751d5ccd932b.png

前半部分，影响挖矿难度的主要是“基础调整”的公式；难度炸弹爆炸的时候，挖矿难度由它决定，剧增，使得人们转向PoS的证明共识。但是由于研究设计PoS遇到问题，不得不回调难度炸弹的区块数，又出现了此后的情况。

ETH的发展阶段

14d6c7d1443c43e79210d1858ad5c89d.png

BIP（BitCoin Improvement Proposal）

在下调挖矿难度（难度炸弹的回调）的同时要下调挖矿的收入，这是为了

  1. 让之前较难时候挖到区块的矿工承受的住一夜之间难度骤减的心理冲击，得到一些心理安慰。

  2. 同时也维持了挖出货币的总供应量

代码实现

拜占庭阶段计算挖矿难度的调整代码

// calcDifficultyByzantium is the difficulty adjustment algorithm.
// It returns the difficulty that a new block should have when created at the given time,
// given the parent block's time and difficulty. The calculation uses the Byzantium rules.
func calcDifficultyByzantium(time uint64, parent *types.Header) *big.Int {
    // https://github.com/ethereum/EIPs/issues/100
    // algorithm:
    // diff = (parent diff + (parent diff / 2048 * max((2 if len(parent.uncles) else 1) * ((timestamp - parent.timestamp) * 0.9), -99)) + 2^(periodcount-2)
    bigTime := new(big.Int).SetUint64(time)
    bigParentTime := new(big.Int).Set(parent.Time)
    x := new(big.Int)
    y := new(big.Int)
    // More code goes here...
}

基础部分计算

// calcDifficultyByzantium is the difficulty adjustment algorithm.
// It returns the difficulty that a new block should have when created at the given time,
// given the parent block's time and difficulty. The calculation uses the Byzantium rules.
func calcDifficultyByzantium(time uint64, parent *types.Header) *big.Int {
    // https://github.com/ethereum/EIPs/issues/100
    // algorithm:
    // diff = (parent diff + (parent diff / 2048 * max((2 if len(parent.uncles) else 1) * ((timestamp - parent.timestamp) * 0.9), -99)) + 2^(periodcount-2)
    bigTime := new(big.Int).SetUint64(time)
    bigParentTime := new(big.Int).Set(parent.Time)
    x := new(big.Int)
    y := new(big.Int)
    
    // Calculate x: (2 if len(parent.uncles) else 1) * ((timestamp - parent.timestamp) / 9)
    x.Sub(bigTime, bigParentTime)
    x.Div(x, big.NewInt(9))
    if parent.UncleHash == types.EmptyUncleHash {
        x.Sub(big.NewInt(1), x)
    } else {
        x.Sub(big.NewInt(2), x)
    }
    
    //与-99相比
    // Calculate max((2 if len(parent.uncles) else 1) * ((timestamp - parent.timestamp) / 9), -99) 
    if x.Cmp(big.NewInt(-99)) < 0 {
        x.Set(big.NewInt(-99))
    }
​
    // Calculate y: parent difficulty / 2048
    y.Div(parent.Difficulty, big.NewInt(2048))
​
    // Calculate diff: parent diff + (parent diff / 2048 * max((2 if len(parent.uncles) else 1) * ((timestamp - parent.timestamp) / 9), -99))
    x.Mul(y, x)
    x.Add(parent.Difficulty, x)
​
    // Set minimum difficulty
    if x.Cmp(big.NewInt(131072)) < 0 {
        x.Set(big.NewInt(131072))//难度下限
    }
​
    return x
}

难度炸弹计算

// Calculate a fake block number for the ice-age delay:
// https://github.com/ethereum/EIPs/pull/669
// Fake block number = min(0, block.number - 3,000,000)
fakeBlockNumber := new(big.Int)
if parent.Number.Cmp(big.NewInt(2999999)) >= 0 {//判断的是负区块的序号
    fakeBlockNumber.Sub(parent.Number, big.NewInt(2999999))
}
​
// For the exponential factor:
periodcount := new(big.Int).Set(fakeBlockNumber)
periodcount.Div(periodcount, expDiffPeriod)
​
// The exponential factor, commonly referred to as "the bomb":
// diff = diff + 2^(periodcount - 2)
if periodcount.Cmp(big.NewInt(1)) > 0 {
    expDiffPeriod := big.NewInt(100000)
    y := new(big.Int).Sub(periodcount, big.NewInt(2))
    y.Exp(big.NewInt(2), y, nil)
    x.Add(x, y)//x 基础部分难度  y  难度炸弹的附加难度
}

 

 

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1684786.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

如何保护Kubernetes集群

如何保护Kubernetes集群

2018年黑客入侵了特斯拉在亚马逊上的Kubernetes容器集群。由于该集群控制台未设置密码保护&#xff0c;黑客便得以在一个Kubernetes pod中获取到访问凭证&#xff0c;然后据此访问其网络存储桶S3&#xff0c;通过S3获取到了一些敏感数据&#xff0c;比如遥测技术&#xff0c;并…
阅读更多...
llama-factory学习个人记录

llama-factory学习个人记录

框架、模型、数据集准备 1.llama-factory部署 # 克隆仓库 git clone https://github.com/hiyouga/LLaMA-Factory.git # 创建虚拟环境 conda create --name llama_factory python3.10 # 激活虚拟环境 conda activate llama_factory # 安装依赖 cd LLaMA-Factory pip install -…
阅读更多...
Vue——开发前的准备和创建一个vue的工程

Vue——开发前的准备和创建一个vue的工程

文章目录 前言安装 Node js1、下载node.js2、安装node.js3、查看是否安装成功 创建 vue 工程Visual Studio Code 配置目录结构 前言 本篇博客主要讲解Vue开发前的环境配置与一些说明。 安装 Node js 环境需要安装配置一个nodejs 的环境。 vue3 最低nodejs 版本要求为 15.0 1…
阅读更多...
2024.5.1学习记录

2024.5.1学习记录

1、代码随想录&#xff1a;贪心刷题 2、react 高级使用( hoc render、props、函数组件、serState 传送门等) 3、游山玩水
阅读更多...
linux部署rustdesk

linux部署rustdesk

1.拉取RustDesk镜像 sudo docker image pull rustdesk/rustdesk-server2.启动hbbs服务 sudo docker run --name hbbs -p 21115:21115 -p 21116:21116 -p 21116:21116/udp -p 21118:21118 -v pwd:/root -td --nethost rustdesk/rustdesk-server hbbs3.启动hbbr服务 sudo dock…
阅读更多...
sqli-labs靶场

sqli-labs靶场

less---11 1.求闭合字符 输入1报错说明存在注入点 存在注入点 2.查库名 使用报错注入查库名 admin” and (select 1 from (select count(*),concat(database(),floor(rand(0)*2))x from information_schema.tables group by x)y)# //floor函数报错 3.查表名 admin and upd…
阅读更多...
一、QGroundControl地面站使用介绍

一、QGroundControl地面站使用介绍

文章目录 环境功能介绍飞行视图规划视图飞机设置分析工具程序设置 连接飞机飞机设置分析工具飞行视图规划任务 总结参考 环境 QGroundControl V4.2.0PX4-Autopilot V1.3.0devGazebo 模拟无人机 功能介绍 飞行视图规划视图飞机设置分析工具程序设置 飞行视图 软件打开后为飞…
阅读更多...
OWASP Benchmark | OWASP 基准项目介绍

OWASP Benchmark | OWASP 基准项目介绍

1. 背景 市面上的静态代码检测SAST工具越来越多&#xff0c;除了业界比较知名的Coverity、Fortify、CheckMax&#xff0c;还有CodeQL、SonarQube、CppCheck等&#xff0c;国内也涌现了一大波检测工具&#xff0c;如鸿渐SAST、奇安信代码卫士、北大Cobot、酷德啄木鸟等&#xf…
阅读更多...
KT142C语音芯片音量详细汇总 包含记忆 低功耗的音量_开机音量

KT142C语音芯片音量详细汇总 包含记忆 低功耗的音量_开机音量

关于KT142C语音芯片sop16的音量详细汇总&#xff0c;包含记忆&#xff0c;低功耗唤醒之后的音量&#xff0c;开机音量 芯片的音量是分为三部分&#xff0c;详见手册的“3.4.2”章节 串口发送指令设置&#xff0c;但是掉电或者进入低功耗被唤醒&#xff0c;这两种情况都会恢复到…
阅读更多...
nvm介绍、下载、安装、配置及使用，(Node Version Manager)nodejs版本管理切换工具

nvm介绍、下载、安装、配置及使用，(Node Version Manager)nodejs版本管理切换工具

1、介绍nvm 在Web前端项目开发过程中&#xff0c;由于各种前端框架、插件 以及 Nodejs、Npm 的飞速更新&#xff0c;在项目新开发 或 对老项目进行更新维护时&#xff0c;有些项目版本的配置 和 当前Node、Npm环境不匹配&#xff0c;导致运行报错&#xff0c;甚至都无法启动。…
阅读更多...
代码随想录算法训练营第二天| 977.有序数组的平方 、209.长度最小的子数组、 59.螺旋矩阵II

代码随想录算法训练营第二天| 977.有序数组的平方 、209.长度最小的子数组、 59.螺旋矩阵II

977. 有序数组的平方 题目链接&#xff1a;977. 有序数组的平方 文档讲解&#xff1a;代码随想录 状态&#xff1a;so easy 刚开始看到题目第一反应就是平方之后进行排序&#xff0c;数据量在 1 0 4 10^4 104&#xff0c;可以使用O(nlogn)的排序。但是更好的方式是使用双指针&a…
阅读更多...
Java面试八股之什么是死锁

Java面试八股之什么是死锁

什么是死锁 死锁&#xff08;Deadlock&#xff09;是多线程编程中的一种常见问题&#xff0c;特别是在涉及到资源共享和同步的时候。具体来说&#xff0c;死锁是指两个或两个以上的线程在执行过程中&#xff0c;由于互相持有并等待对方释放的资源&#xff0c;而导致所有线程都…
阅读更多...
Centos7.9上安装Oracle 11gR2 RAC 三节点（ASMlib管理asm磁盘）

Centos7.9上安装Oracle 11gR2 RAC 三节点（ASMlib管理asm磁盘）

服务器规划 OS 规格 主机名 IP VIP private IP scanip centos 7.9 1C4G racdb01 192.168.40.165 192.168.183.165 192.168.40.16 192.168.40.200 centos 7.9 1C4G racdb02 192.168.40.175 192.168.183.175 192.168.40.17 192.168.40.200 centos 7.9 1C4G…
阅读更多...
php题解（巩固基础知识）代码审计

php题解（巩固基础知识）代码审计

1.[NISACTF 2022]easyssrf 1&#xff09;进入环境后&#xff0c;他给了一个上url个文本框 2&#xff09;看了源码&#xff0c;没啥用&#xff0c;那就直接跟着它提示走&#xff0c;输入一个网址http://127.0.0.1/flag.php 3&#xff09;回显又给了/fl4g&#xff0c;直接file…
阅读更多...
微服务：Ribbon负载均衡与加载时机修改

微服务：Ribbon负载均衡与加载时机修改

Ribbon 负载均衡 执行流程 负载均衡策略 调整负载均衡方案&#xff1a; 配置类中&#xff08;全局&#xff09;&#xff1a; // 负载均衡策略Beanpublic IRule randomRule() {return new RandomRule();}yaml配置 userservice: # 给某个微服务配置负载均衡规则&#xff…
阅读更多...
【UE HTTP】“BlueprintHTTP Server - A Web Server for Unreal Engine”插件使用记录

【UE HTTP】“BlueprintHTTP Server - A Web Server for Unreal Engine”插件使用记录

1. 在商城中下载“BlueprintHTTP Server - A Web Server for Unreal Engine”插件 该插件的主要功能有如下3点&#xff1a; &#xff08;1&#xff09;监听客户端请求。 &#xff08;2&#xff09;可以将文件直接从Unreal Engine应用程序提供到Web。 &#xff08;3&#xff…
阅读更多...
elementui中 表格使用树形数据且固定一列时展开子集移入时背景色不全问题

elementui中 表格使用树形数据且固定一列时展开子集移入时背景色不全问题

原来的效果 修改后实现效果 解决- 需要修改elementui的依赖包中lib/element-ui.common.js中的源码 将js中此处代码改完下面的代码 watch: {// dont trigger getter of currentRow in getCellClass. see https://jsfiddle.net/oe2b4hqt/// update DOM manually. see https:/…
阅读更多...
Oracle体系结构初探：数据库启动与停止

Oracle体系结构初探：数据库启动与停止

往期内容 参数管理 控制文件添加 启动 在启动Oracle数据库时&#xff0c;我们一般会使用如下命令&#xff1a; startup 虽然命令只有一个&#xff0c;但其中却是经历了3个阶段&#xff0c;从下面执行 startup 命令返回也可以看出来。 总结为3个阶段&#xff1a; nomount&…
阅读更多...
【Unity2D 2022：Cinemachine】相机跟随与地图边界

【Unity2D 2022：Cinemachine】相机跟随与地图边界

一、导入Cinemachine工具包 1. 点击Window-Package Manager&#xff0c;进入包管理界面 2. 点击All&#xff0c;找到Cinemachine工具包&#xff0c;点击Install 二、相机跟随角色 1. 选中Main Camera&#xff0c;点击Component-Cinemachine-CinemachineBrain&#xff0c;新建…
阅读更多...
【stm32/CubeMX、HAL库】嵌入式实验五：定时器(2)|PWM输出

【stm32/CubeMX、HAL库】嵌入式实验五：定时器(2)|PWM输出

参考&#xff1a; 【【正点原子】手把手教你学STM32CubeIDE开发】 https://www.bilibili.com/video/BV1Wp42127Cx/?p13&share_sourcecopy_web&vd_source9332b8fc5ea8d349a54c3989f6189fd3 《嵌入式系统基础与实践》刘黎明等编著&#xff0c;第九章定时器&#xff0c…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023