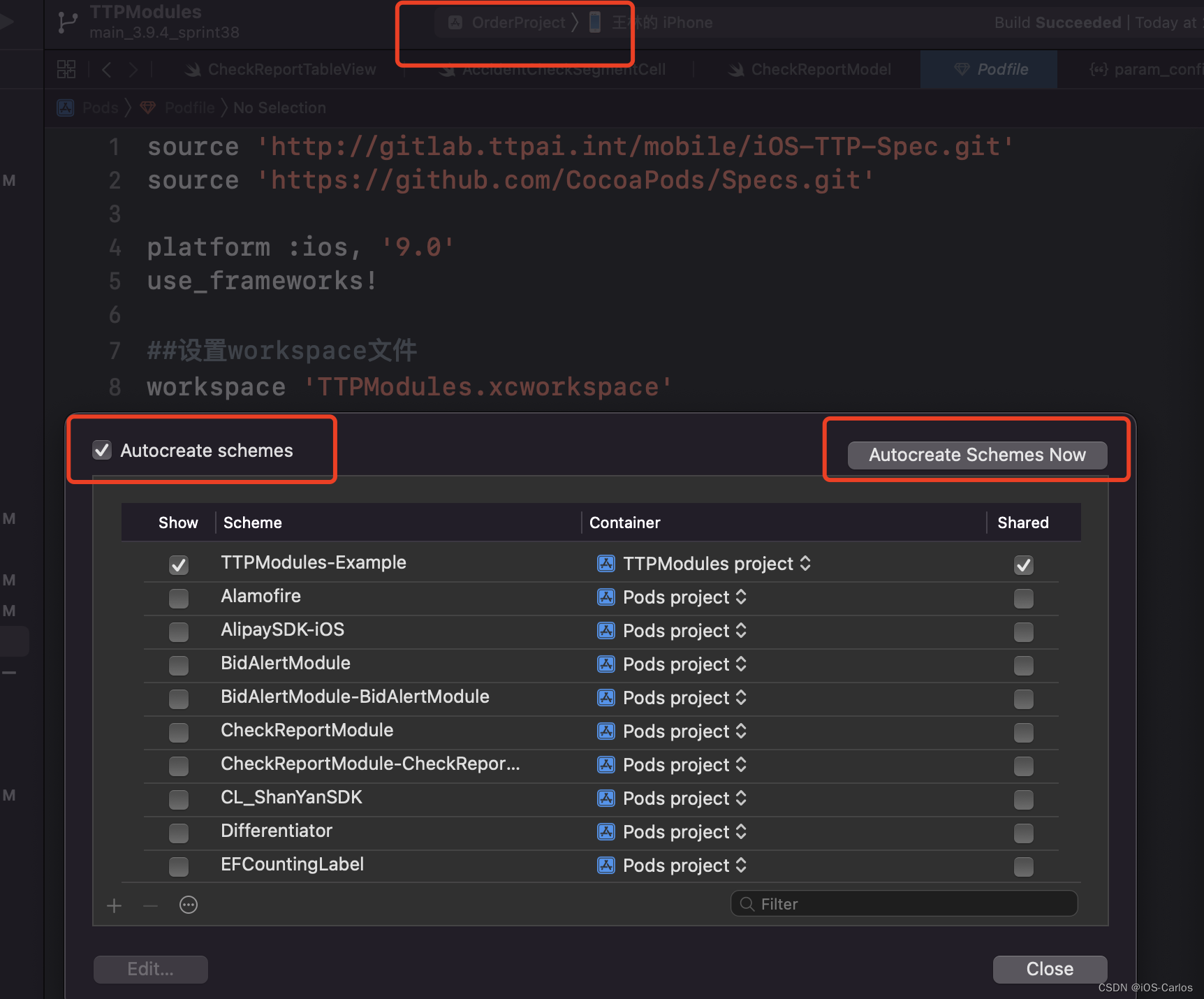
1.block内相邻元素规约（线程不连续）

 上图为1个block内的16个线程的操作示意：

第0个线程会和第1，2，4，8发生关系

第2个线程会和第3个线程发生关系

第4个线程会和第5，6个线程发生关系

...

以上规律就是满足t%(2*stride)==0，stride为1，2，4，8。。。。直到stride大于block总线程数

#define THREAD_LENGTH 1024
__global__ void reduceSum(double *d_A, int n){
    unsigned int t = threadIdx.x;// 获取block内线程编号
    unsigned int idx = blockIdx.x*blockDim.x + t;//获取grid内总的线程编号
    __shared__ double partialSum[THREAD_LENGTH];
    if(blockIdx.x*blockDim.x + t < n)
        partialSum[t] = d_A[idx];
    else 
        partialSum[t] = 0;
    __syncthreads();  //将数组加载到共享存储器。
    for(unsigned int stride = 1; stride < blockDim.x; stride *= 2){
        if(t % (2*stride) == 0) //指令分化没法保证warp统一计算
            partialSum[t] += partialSum[t + stride];
        __syncthreads();//等前面没有东西算了再加起来
    }
    if(t == 0)   
        d_A[idx] = partialSum[t];//把每个block求和结果写入到每个block的第一个位置。
}

 该方法导致活动指令不是连续的，计算核闲置较多，不利于并行加速。

2.block内相邻元素规约（线程连续,bank不连续）

 前面是第几个线程就访问对应位置的数据，现在我们为了要连续线程内操作不分化，所以考虑让连续线程访问不同位置的数据：

stride=1: 让线程0～7，访问第1，3，5，7，9个数字，

stride=2: 让线程0～3，访问第1，4，8, 12个数字

....

__global__ void reduceSum1(double *d_A, int n){
    unsigned int t = threadIdx.x;// 获取block内线程编号
    unsigned int idx = blockIdx.x*blockDim.x + t;//获取grid内总的线程编号
    __shared__ double partialSum[THREAD_LENGTH];
    if(blockIdx.x*blockDim.x + t < n)
        partialSum[t] = d_A[idx];
    else 
        partialSum[t] = 0;
    __syncthreads();  //将数组加载到共享存储器。
    for(unsigned int stride = 1; stride < blockDim.x;  stride*= 2)
    {
        int index = 2*stride*t;
        if(index<blockDim.x)
            partialSum[index] += partialSum[index + stride];
        __syncthreads();
    }
    if(t == 0)   
        d_A[idx] = partialSum[t];
}

  该方法可以保证活动指令具有连续性，但是地址访问不连续。

3.交错配对规约

 该方法可以保证连续线程执行的指令一致，而且数据地址访问也连续，比较有利于并行

以图为例，第0～7个线程，让第0～7和第8～15数字相关（stride=8）

然后第0～3个线程，让第0～3和4～7个数字相关。（stride=4)

既数据前半部和后半部相关，以此类推。

__global__ void reduceSum2(double *d_A, int n)
{
    unsigned int t = threadIdx.x;// 获取block内线程编号
    unsigned int idx = blockIdx.x*blockDim.x + t;//获取grid内总的线程编号
    __shared__ double partialSum[THREAD_LENGTH];
    if(blockIdx.x*blockDim.x + t < n)
        partialSum[t] = d_A[idx];
    else 
        partialSum[t] = 0;
    __syncthreads();  //将数组加载到共享存储器。
    for(unsigned int stride = blockDim.x/2; stride>0;  stride/= 2)
    {
        if(t<stride)
            partialSum[t] += partialSum[t + stride];
        __syncthreads();
    }
    if(t == 0)   
        d_A[idx] = partialSum[t];

}

这样同时保证了wrap内指令的一致，也保证了bank的访问连续，该方法在绝大多数情况基本已经可以满足要求了，但是其实在kernel执行时，也会有1半的线程空闲，所以还可以继续优化。