难度分布
根据排行榜情况,大致分布如下:
Easy:AIDE
Middle:CJF
Hard:GBH
题解
A. Hello World.(题意实现)
直接输出Hello world.
I. lgl想签到(题意实现)
统计周一到周六晚上同时学习和打游戏的天数
周日同时学习和打游戏会导致下周一迟到,不计入本周
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int a[N],cnt,c;
int main(){
//while(cin>>a[++c]);
//assert(c==15);
for(int i=1;i<=14;++i)cin>>a[i];
for(int i=1;i<7;++i){
if(a[i]==1 && a[i+7]==1)cnt++;
}
cout<<cnt<<endl;
return 0;
}D. 位数相加(思维,规律)
记一个数i迭代若干次之后,最终得到的个位数的结果是g(i)
打表发现,g(i)呈1、2、3、4、5、6、7、8、9的循环分布
所以一定是1>=2,只需判断g(n)=1是否成立,g(n)=1说明1多一个,否则相等
而注意到n%9也呈0、1、2、3、4、5、6、7、8的循环分布,且g(1)%9=1%9
所以,要判断g(n)=1,只需判断n%9=1是否成立即可
#include<bits/stdc++.h>
using namespace std;
int n;
int main(){
cin>>n;
assert(1<=n && n<=1000000000);
if(n%9==1)cout<<"1>2";
else cout<<"1=2";
return 0;
}
/*
#include<bits/stdc++.h>
using namespace std;
int n;
int f(int x){
int ans=0;
for(;x>0;x/=10)ans+=x%10;
return ans;
}
int main(){
cin>>n;
assert(1<=n && n<=1000000000);
while(n/10)n=f(n);
if(n==1)cout<<"1>2";
else cout<<"1=2";
return 0;
}
*/E. 沙(思维)
按题意,先把x=1和x=n这两个元素去掉,不统计,剩余n-2个元素
1. 如果k=1,可以单点加,则可以令其中一半上取整个,使之满足要求
2. 如果k>=2,设操作了至少一次,且同时操作了a[i]和a[i-1],令其+1,
再比较a[i]和a[i-1]+a[i+1]的大小时,发现a[i]-(a[i-1]+a[i+1])不变,
如果同时操作了a[i]、a[i-1]、a[i+1],发现a[i]-(a[i-1]+a[i+1])变得更小了,
所以不如不操作,直接统计初始局面的合法元素个数
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n,k,a[N],cnt;
int main(){
cin>>n>>k;
assert(3<=n && n<=100000);
assert(1<=k && k<=n);
for(int i=1;i<=n;++i){
cin>>a[i];
assert(0<=a[i] && a[i]<=1000000000);
}
if(k==1){
n-=2;
cout<<(n+1)/2<<endl;
return 0;
}
for(int i=2;i<n;++i){
if(a[i]>a[i-1]+a[i+1]){
cnt++;
}
}
cout<<cnt<<endl;
return 0;
}C. 深度学习(题意实现)
按照题面描述模拟即可,
分类讨论了一下补一圈0的情况
#include<bits/stdc++.h>
using namespace std;
const int N=105+10;
int m,x,y,p,a[N][N],b[N][N];
int main(){
cin>>m>>x>>y>>p;
assert(3<=m && m<=100);
assert(1<=x && x<=100);
assert(1<=y && y<=100);
assert(0<=p && p<=1);
if(p==1){
m+=2;
for(int i=2;i<m;++i){
for(int j=2;j<m;++j){
cin>>a[i][j];
assert(0<=a[i][j] && a[i][j]<=30);
}
}
}
else{
for(int i=1;i<=m;++i){
for(int j=1;j<=m;++j){
cin>>a[i][j];
assert(0<=a[i][j] && a[i][j]<=30);
}
}
}
for(int i=1;i<=x;++i){
for(int j=1;j<=y;++j){
cin>>b[i][j];
assert(0<=b[i][j] && b[i][j]<=30);
}
}
for(int i=1;i+x-1<=m;++i){
for(int j=1;j+y-1<=m;++j){
int cnt=0;
for(int k=i;k<=i+x-1;++k){
for(int l=j;l<=j+y-1;++l){
cnt+=a[k][l]*b[k-i+1][l-j+1];
}
}
cout<<cnt;
if(j+y-1==m)cout<<endl;
else cout<<" ";
}
}
return 0;
}J. lgl学图论(最短路)
最短路 - OI Wiki板子题,用dijkstra跑1号点出发的单源最短路即可,
数据范围1e6,需要堆优化,注意图可能不连通,注意重边和自环
#include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> P;
const int N=1e6+10,INF=0x3f3f3f3f;
int n,m,u,v,w,dis[N];
bool vis[N];
vector<P>e[N];
struct Q{
int d,u;
Q(){}
Q(int dd,int uu):d(dd),u(uu){}
};
bool operator<(Q a,Q b){
return a.d>b.d;
}
priority_queue<Q>q;
void dijkstra(int s){
memset(dis,INF,sizeof dis);
q.push(Q(0,s));
dis[s]=0;
while(!q.empty()){
Q z=q.top();q.pop();
int d=z.d,u=z.u;
if(vis[u])continue;
vis[u]=1;
for(auto &x:e[u]){
int v=x.first,w=x.second;
if(dis[v]>dis[u]+w){
dis[v]=dis[u]+w;
q.push(Q(dis[v],v));
}
}
}
}
signed main(){
scanf("%d%d",&n,&m);
assert(1<=n && n<=1000000);
assert(1<=m && m<=1000000);
for(int i=1;i<=m;++i){
scanf("%d%d%d",&u,&v,&w);
assert(1<=u && u<=n);
assert(1<=v && v<=n);
assert(1<=w && w<=1000);
if(u==v)continue;
e[u].push_back(P(v,w));
e[v].push_back(P(u,w));
}
dijkstra(1);
for(int i=1;i<=n;++i){
printf("%d%c",dis[i]==INF?-1:dis[i]," \n"[i==n]);
}
return 0;
}F. 瞄准(数论)
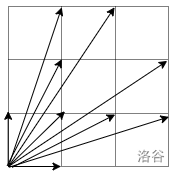
欧拉函数板子题,
注意到答案除了(1,1)点以外,其他点是关于直线y=x对称的
所以可以统计某一半的答案,记为ans,则最终答案为2*ans+1
不妨统计直线y=x以下部分(y<x)的答案,
如果两个(x,y)的点的斜率相同,则只能被统计一次,
换言之,需要满足被统计到答案内的y/x,是最简分数,
且注意到被统计的那一次x和y互质,即统计:
,
其中,额外加上的1,是(1,0)这个点
根据欧拉函数定义,这就是:
所以,预处理欧拉函数及其前缀和,对于每个询问O(1)回答即可
1e6,用线性筛或者类似埃筛的O(nlogn)写法均可通过
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6+10,mod=998244353;
bool ok[N];
int t,n,prime[N],phi[N],cnt;
void sieve(){
phi[1]=1;
for(ll i=2;i<N;++i){
if(!ok[i]){
prime[cnt++]=i;
phi[i]=i-1;
}
for(int j=0;j<cnt;++j){
if(i*prime[j]>=N)break;
ok[i*prime[j]]=1;
if(i%prime[j]==0){
phi[i*prime[j]]=phi[i]*prime[j];//prime[j]是i的因子 prime[j]的素因子项包含在i的素因子项里
break;
}
else phi[i*prime[j]]=phi[i]*(prime[j]-1);//prime[j]与i互质 phi[i*prime[j]=phi[i]*phi[prime[j]]
}
}
for(int i=2;i<N;++i){
phi[i]=(phi[i-1]+phi[i])%mod;
}
}
int main(){
sieve();
cin>>t;
assert(1<=t && t<=1000000);
while(t--){
cin>>n;
assert(1<=n && n<=1000000);
int ans=(2ll*phi[n]+1)%mod;
cout<<ans<<endl;
}
return 0;
}G. 魔方物品(动态规划)
分两种情况,即打折和不打折,
如果打折的话,最优的操作是把某一个魔法物品最后放入,让前面的物品都打折
1. 不打折,直接做完全背包
2. 打折,对体积>=C的物品做一次01背包,表示必取的最后一个物品,然后再对所有物品做体积为6/7的完全背包,表示前面取的物品
注意此时由于体积>=C的物品必取,前驱只能从做过01背包的值转移而来,
这里由于每个物品的val>0,就只能从>0的dp值转移而来
看了出题人的题解,最后一个物品枚举就行了,做什么01背包
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e4+10,M=1e6+10;
int n,v,c,a[N],b[N];
ll dp[M],ans;
int main(){
cin>>n>>v>>c;
assert(1<=n && n<=10000);
assert(1<=c && c<=v && v<=1000000);
ll w=1ll*n*v;
assert(1<=w && w<=10000000);
for(int i=1;i<=n;++i){
cin>>a[i]>>b[i];
assert(7<=a[i] && a[i]<=10000);
assert(a[i]%7==0);
assert(1<=b[i] && b[i]<=1000000);
for(int j=a[i];j<=v;++j){
dp[j]=max(dp[j],dp[j-a[i]]+b[i]);
}
}
ans=dp[v];
memset(dp,0,sizeof dp);
for(int i=1;i<=n;++i){
if(a[i]>=c){
for(int j=v;j>=a[i];--j){
dp[j]=max(dp[j],dp[j-a[i]]+b[i]);
}
}
}
for(int i=1;i<=n;++i){
a[i]/=7;a[i]*=6;
for(int j=a[i];j<=v;++j){
if(dp[j-a[i]]>0)dp[j]=max(dp[j],dp[j-a[i]]+b[i]);
}
}
ans=max(ans,dp[v]);
cout<<ans<<endl;
return 0;
}B. 恐怖的期末考试月(思维 二分/逆序贪心)
本题是Codeforces Round #808 (Div. 2) C题的减弱版,可以二分或逆序考虑
做法1(二分):
如果q>=n显然全取,否则最终智商一定为0,
而{第i天减1,后面提前减为0,导致最后的有一些不选},
显然是不如{把第i天减1的机会往后挪,这样有可能能有更多的可以选},
所以,可以二分天数x,即二分找到这样的最小的第x天,
使得第[1,x)天需要降智的不选,不需要降智的选,
而第[x,n]天全选,该降智就降智,这些天里恰能把q次降智机会都用完,
用不完就向更小的天数二分,直到q次能用完,或者x=1。
做法2(逆序贪心):
如果q>=n显然全取,否则最终智商一定为0,显然降的机会发生在后面是更优的。
逆序看待这个过程,把顺序的降认为是逆序的升,顺序的不操作认为是逆序的不操作,
就可以直接贪心了,初始智商0,能升智就升智,因为这样天数越小,智商越高。
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n,q,a[N],now,cnt;
int main(){
cin>>n>>q;
assert(1<=n && n<=100000);
assert(1<=q && q<=1000000000);
for(int i=1;i<=n;++i){
cin>>a[i];
assert(0<=a[i] && a[i]<=1000000000);
}
if(q>=n){
cout<<n<<endl;
return 0;
}
for(int i=n;i>=1;--i){
if(a[i]>now){
if(now<q)now++,cnt++;
}
else{
cnt++;
}
}
cout<<cnt<<endl;
return 0;
}H. Robot(动态规划/线段树)
xjb乱搞搞过去了,评价是不如直接看出题人的题解
注意到走法只有以下三种情况,
而后两种情况,需要在每个决策点(如:(0,0),(0,2),etc...)的时候都要考虑
换言之,走法一定由两部分组成,左半段蛇形走位(可能为空),右半段直线走位(可能为空)
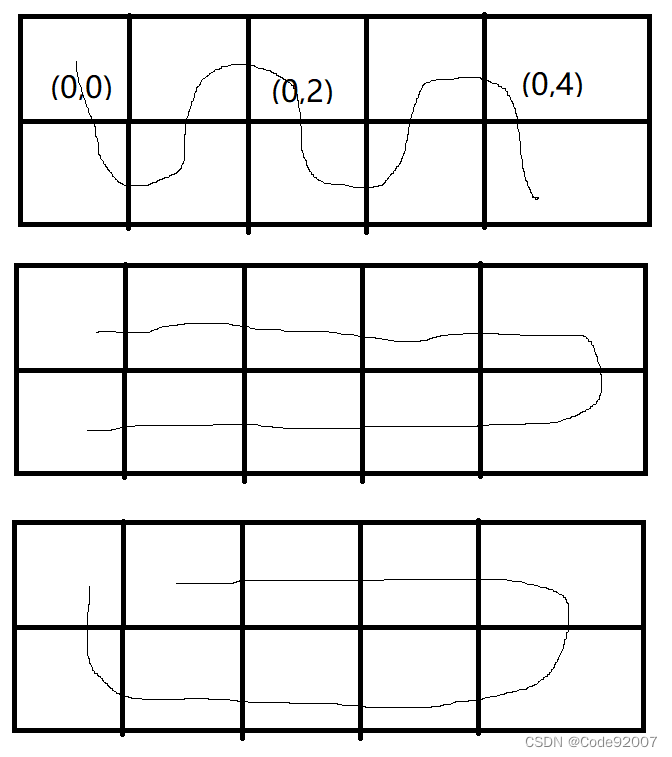
考虑每个点(i,j)对最终时间的独立的贡献,是a[i][j]+1+走完(i,j)之后走的点的个数,
由于会因为一些点block住,最终的时间一定是所有点的贡献取max
基于此,有两种做法,可以求出直线走位,即后半程的点的贡献的最大值
1. dp是倒着预处理,只考虑第i列及其往右的部分,
从右往左递推出,第i列一头作为起止点,另一头作为终点的最早扫完时间
因为是直线走位,a[0][i]作为起止点,则a[1][i]为终点,反之同理,维护两个dp数组
2. 而线段树是正着硬莽,从左往右暴力扫
维护的信息与上面dp的相同,求出i列一头作为起止点,另一头作为终点的最早扫完时间
因为蛇形一次走两列,所以求第i+2列的答案的时候,需要对当前第i列的答案暴力区间减2
开了两棵线段树,单点赋值,区间减,区间求max
从左往右,枚举蛇形走位和直线走位的分界点,
蛇形走位的部分模拟即可,即先等到可以走的时候,cur=max(cur,a[i][j]),再走,cur++
后半直线走位的部分,用预处理的dp值,或用线段树现查的结果,
时间是前半段走完和后半段走完的max,于所有可能性中取最短时间,即为答案
写了一个半小时,不过感觉当个压轴题还可以,没脑子,没想到用dp
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+10;
int m,a[2][N],ans=2e9,cur;
struct segtree{
int n;
struct node{int l,r,v,c;}e[N<<2];
#define l(p) e[p].l
#define r(p) e[p].r
#define v(p) e[p].v
#define c(p) e[p].c
void up(int p){v(p)=max(v(p<<1),v(p<<1|1));}
void bld(int p,int l,int r){
l(p)=l;r(p)=r;
if(l==r){v(p)=c(p)=0;return;}
int mid=l+r>>1;
bld(p<<1,l,mid);bld(p<<1|1,mid+1,r);
up(p);
}
void psd(int p){
if(c(p)){
v(p<<1)+=c(p);
c(p<<1)+=c(p);
v(p<<1|1)+=c(p);
c(p<<1|1)+=c(p);
c(p)=0;
}
}
void init(int _n){n=_n;bld(1,1,n);}
void chg(int p,int x,int v){
if(l(p)==r(p)){v(p)=v;return;}
int mid=l(p)+r(p)>>1;
psd(p);
chg(p<<1|(x>mid),x,v);
up(p);
}
void add(int p,int ql,int qr,int v){
if(ql>qr)return;
if(ql<=l(p)&&r(p)<=qr){
v(p)+=v;
c(p)+=v;
return;
}
psd(p);
int mid=l(p)+r(p)>>1;
if(ql<=mid)add(p<<1,ql,qr,v);
if(qr>mid)add(p<<1|1,ql,qr,v);
up(p);
}
int ask(int p,int ql,int qr){
if(ql>qr)return 0;
if(ql<=l(p)&&r(p)<=qr)return v(p);
int mid=l(p)+r(p)>>1,res=0;
psd(p);
if(ql<=mid)res=max(res,ask(p<<1,ql,qr));
if(qr>mid)res=max(res,ask(p<<1|1,ql,qr));
return res;
}
}seg,seg2;
int main(){
cin>>m;
assert(1<=m && m<=100000);
seg.init(2*m);
seg2.init(2*m);
for(int i=0;i<2;++i){
for(int j=0;j<m;++j){
cin>>a[i][j];
assert(0<=a[i][j] && a[i][j]<=1000000000);
if(!i && !j){
assert(!a[0][0]);
continue;
}
//cout<<"i:"<<i<<" j:"<<j<<endl;
if(!i){
seg.chg(1,j+1,a[i][j]+2*m-j);//第j+1个,当前及后面还有2m-j个,二者和为2*m+1,下同
seg2.chg(1,2*m+1-j,a[i][j]+j);
//cout<<"v1:"<<j+1<<" "<<a[i][j]+2*m-j<<endl;
//cout<<"v2:"<<2*m+1-j<<" "<<a[i][j]+j<<endl;
}
else{
seg.chg(1,2*m-j,a[i][j]+j+1);//第2m-j个,当前及后面还有j+1个
seg2.chg(1,j+2,a[i][j]+2*m-1-j);
//cout<<"v1:"<<2*m-j<<" "<<a[i][j]+j+1<<endl;
//cout<<"v2:"<<j+2<<" "<<a[i][j]+2*m-1-j<<endl;
}
}
}
for(int i=0;i<m;i+=2){
int t=cur+2*(m-i)-1;
//cout<<"i:"<<i<<" t0:"<<t<<endl;
t=max(t,min(seg.ask(1,i+2,2*m-i),seg2.ask(1,i+2,2*m-i)));
//cout<<"i:"<<i<<" t1:"<<t<<endl;
ans=min(ans,t);
cur=max(cur,a[1][i]),cur++;
if(i+1<m)cur=max(cur,a[1][i+1]),cur++;
if(i+1<m)cur=max(cur,a[0][i+1]),cur++;
if(i+2<m)cur=max(cur,a[0][i+2]),cur++;
if(i+2>=m)break;
seg.add(1,i+2,2*m-i,-2);
seg2.add(1,i+2,2*m-i,-2);
}
//cout<<"cur:"<<cur<<endl;
ans=min(ans,cur);
cout<<ans<<endl;
return 0;
}个人感受
验题人(×)赛中开管理员号同步做题的(√)
感觉思维题居多,码量较小,
一些知识点(如:数论、最短路等)也有考察,有一些板子题,比较适合新生赛