《深度学习入门:基于python的理论与实现》chap2 感知机笔记

3个月前正式开始入坑AI的时候就是看的这本书，当时比较粗略地看到了第六章，没有记笔记，现在来重温一下

文章目录

《深度学习入门:基于python的理论与实现》chap2 感知机笔记
2.1 什么是感知机
2.2 简单逻辑电路 &2.3 感知机的实现
- 引入偏置
- 与门 And gate
- 与非门(NAND gate)
- 或门 OR gate
2.4 感知机的局限性(单层感知机无法分离非线性空间)
- 2.4.1 异或门
- 2.4.2 线性和非线性
2.5 多层感知机(multi-layered perception)
- 2.5.1 已有门电路的组合
- 2.5.2 异或门的实现
2.6 从与非门到计算机
2.7 小结

本chap学习感知机(perceptron)这一算法并利用感知机解决一些简单的问题。感知机是由美国学者Frank Rosenblatt在1957年提出来的。

严格地讲，本章中所说的感知机应该称为“人工神经元”或“朴素感知机”，但是因为很多基本的处理都是共通的，所以这里就简单地称为“感知机”。

Frank Rosenblatt is known for his work in the field of artificial intelligence and is credited with creating one of the first artificial neural networks, called the perceptron. The perceptron was a simple algorithm designed to simulate the process of human perception and was presented in 1957 by Frank Rosenblatt at Cornell Aeronautical Laboratory in a paper called “The Perceptron: A Probabilistic Model for Information Storage and Organization in The Brain”

The perceptron was able to classify linearly separable patterns, which means it could learn to separate two classes of data with a straight line. Later research showed that the perceptron algorithm could not solve certain types of problems, such as the XOR problem, and that more complex neural networks were needed to solve these problems. However, this work of Rosenblatt inspired many other researchers to continue exploring the potential of neural networks and machine learning.

2.1 什么是感知机

既然是再次看这本书，就尝试自己总结和概况

我觉得学习计算机要实时秉持输入经过某个function得到输出的观念，感知机，从字面上看，感知一些东西，经过某个function，做出反应，那么感知的东西就是输入，作出的反应就是输出

那么输入是什么呢？
- 感知机会接收信号，这里的信号取值是0或1
  - 0对应不传递信号
  - 1对应传递信号
function是什么？
- 使得每个输入信号乘以其固定的权重(weight)再相加
输出是什么？
- 这些信号分别与他们的权重相乘之后再相加的结果，也作为一个信号输出，也是0或1
- 那么什么情况会输出1(称为"神经元被激活")，什么时候输出0呢
  - 前面说的相加的结果，也就是信号的总和，会和一个界限值进行比较，这个界限值称为阈值(threshold)

图示和数学表达式
- 图示
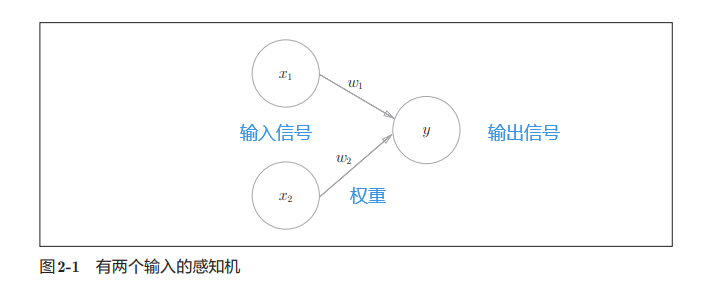
- 数学表达式

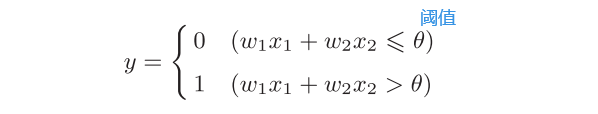
2.2 简单逻辑电路 &2.3 感知机的实现

引入偏置

把前面的式子变一变，这里把−θ命名为偏置b,偏置的值决定了神经元被激活的容易程度。

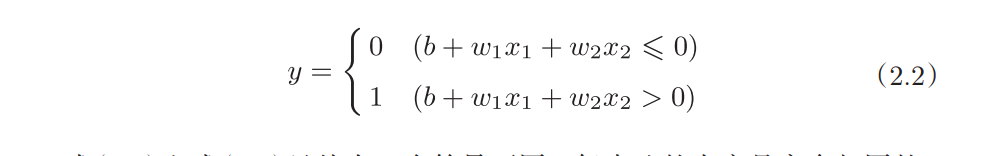
w1和w2是控制输入信号的重要性的参数，而偏置是调整神经元被激活的容易程度（输出信号为1的程度）的参数。

比如，若b为 −0.1，则只要输入信号的加权总和超过0.1，神经元就会被激活。但是如果b 为−20.0，则输入信号的加权总和必须超过20.0，神经元才会被激活。

哈哈在数电里面学过了这些gates，那这里就记录一些英文表达

与门 And gate

我们尝试找一个能实现与门功能的感知机，与门的输入输出我们知道了，那就是要找剩下的几个参数，两个权重和一个阈值

书上给的这个例子 0.5，0.5，0.7

tmp那里是把前面的数学公式右边减到左边来了，当且仅当x1=1,x2=1时，0.5x1+0.5x2>0.7

# coding: utf-8
import numpy as np


def AND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

if __name__ == '__main__':
    for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
        y = AND(xs[0], xs[1])
        print(str(xs) + " -> " + str(y))

(0, 0)->0
(1, 0)->0
(0, 1)->0
(1, 1)->1

有无数组参数都可以做到，比如

    w = np.array([0.6, 0.5])
    b = -0.95

回忆一下数电，输入的0表示低电平，1表示高电平，输出也是两种情况，低电平or高电平
- 中间也是经历了一些计算，不过那个涉及模电了，不是这种简单的感知机

与非门(NAND gate)

NAND ，即Not AND

与非门就是颠倒了与门的输出
要表示与非门，可以用(w1, w2, θ) = (−0.5, −0.5, −0.7) 这样的组合（其他的组合也是无限存在的）。实际上，只要把实现与门的参数值的符号取反，就可以实现与非门

代码实现

# coding: utf-8
import numpy as np


def NAND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([-0.5, -0.5])
    b = 0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1


if __name__ == '__main__':
    for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
        y = NAND(xs[0], xs[1])
        print(str(xs) + " -> " + str(y))

或门 OR gate

我们来思考一下参数，根据或或门的特点，w1和w2都要比θ大，然后θ>=0即可

也就是 0<=θ< min[w1,w2]

θ=-b（代码里面）

code

# coding: utf-8
import numpy as np


def OR(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.2
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1


if __name__ == '__main__':
    for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
        y = OR(xs[0], xs[1])
        print(str(xs) + " -> " + str(y))

2.4 感知机的局限性(单层感知机无法分离非线性空间)

2.4.1 异或门

异或门也被称为逻辑异或电路，x1和x2相同时，输出0，不同时输出1

哈哈哈我记得大一学C语言的时候，异或和同或总是傻傻分不清🤣😓😓😓

前面的感知机能否实现这个异或门呢
之前在凑前几个参数的具体值的时候，我是将00,y ；01,y；10,y；11,y四种情况代入进去分析的
- 那么这里我也尝试代入进去分析(字丑见谅🤐🤐🤐)
再来看看书上是如何分析的
- 将或门的动作形象化。或门的情况下，当权重参数 (b, w1, w2) = (−0.5, 1.0, 1.0)时可满足真值表
  - 感知机会生成由直线−0.5 + x1 + x2 = 0分割开的两个空间。其中一个空间输出1，另一个空间输出0
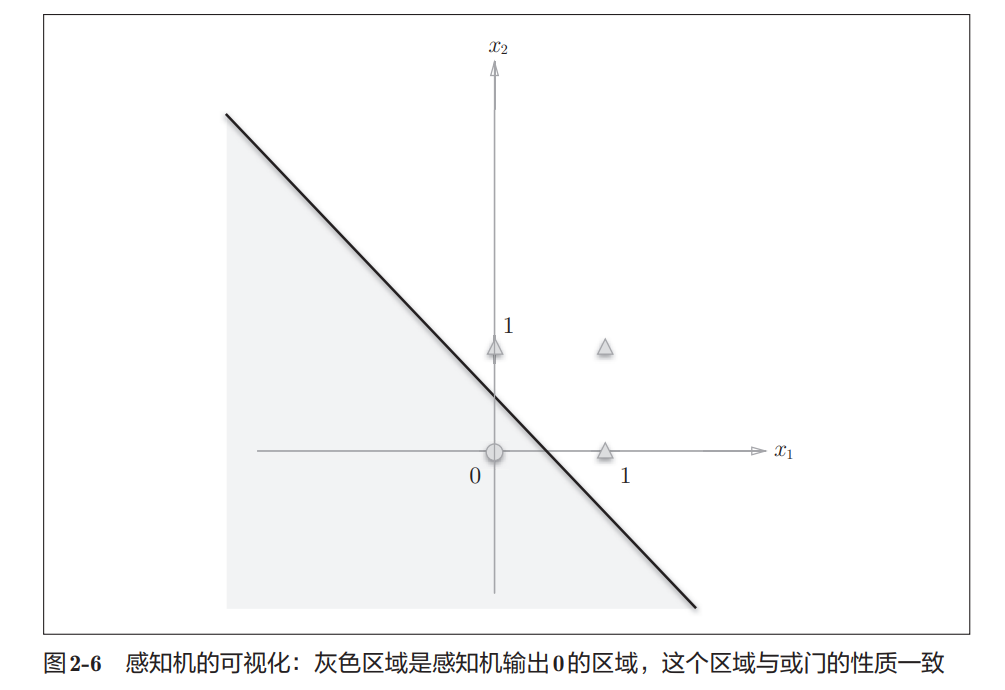
    - 或门在(x1, x2) = (0, 0)时输出0，在(x1, x2)为(0, 1)、(1, 0)、(1, 1)时输出1。图2-6中，○表示0，△表示1
    - 如果想制作或门，需要用直线将图2-6中的○和△分开。实际上，刚才的那条直线就将这4个点正确地分开了
- 换成异或门还能找条直线来分开吗？
  
  其实和我前面推导的式子来理解也一样，直线的斜率一会儿大于0，一会儿小于0，分不开的

2.4.2 线性和非线性

图2-7中的○和△无法用一条直线分开，但是如果将“直线”这个限制条件去掉，就可以实现了。比如，我们可以像图2-8那样，作出分开○和△的空间。
感知机的局限性就在于它只能表示由一条直线分割的空间。图2-8这样弯曲的曲线无法用感知机表示。另外，由图2-8这样的曲线分割而成的空间称为 非线性空间，由直线分割而成的空间称为线性空间。线性、非线性这两个术语在机器学习领域很常见，可以将其想象成图2-6和图2-8所示的直线和曲线。

2.5 多层感知机(multi-layered perception)

虽然无法利用一个感知机直接实现异或门，但是我们能不能叠加多层来实现呢？Yes
- 异或门的制作方法有很多，其中之一就是组合我们前面做好的与门、与非门、或门进行配置
实际上，与门、或门是单层感知机，而异或门是2层感知机。叠加了多层的感知机也称为多层感知机（multi-layered perceptron）

2.5.1 已有门电路的组合

书上给了这种做法

（与非）和（或）再与

2.5.2 异或门的实现

code

# coding: utf-8
from and_gate import AND
from or_gate import OR
from nand_gate import NAND


def XOR(x1, x2):
    s1 = NAND(x1, x2)
    s2 = OR(x1, x2)
    y = AND(s1, s2)
    return y

if __name__ == '__main__':
    for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
        y = XOR(xs[0], xs[1])
        print(str(xs) + " -> " + str(y))