Open CASCADE学习|BRepFill

BRepFill_SectionPlacement 是一个与计算机辅助设计（CAD）相关的术语，通常用于指代一个几何对象或操作，它是Open CASCADE Technology（OCCT）中的一个类。Open CASCADE Technology是一个开源的CAD内核，广泛应用于工业软件中，用于处理3D模型的创建、编辑和数据交换。

在OCCT中，BRepFill_SectionPlacement 类的作用是将一个截面（或称为剖面）放置在特定的位置和方向上。这个类是用于填充操作的一部分，填充操作涉及创建一个3D实体，这个实体是通过将一个2D截面沿着一个路径或导线扫掠（sweep）形成的。

以下是关于 BRepFill_SectionPlacement 类的一些关键点：

截面（Section）：这是填充操作中的2D几何形状，可以是任何形状的轮廓，比如圆形、矩形或其他复杂形状。

放置（Placement）：这定义了截面在3D空间中的确切位置和方向。放置可以通过平移（translation）和旋转（rotation）来指定。

路径（Path）：在某些情况下，截面不是简单地放置在一个位置，而是沿着一个路径移动，从而创建一个更为复杂的3D形状。

生成实体（Generating Solids）：通过 BRepFill_SectionPlacement 可以生成3D实体，这些实体可以是实体的几何形状，如块、圆柱、管道等。

参数化（Parametric）：OCCT中的类通常是参数化的，这意味着它们的行为可以通过设置不同的参数来控制。

API（Application Programming Interface）：BRepFill_SectionPlacement 是OCCT提供的API的一部分，允许开发者在他们的应用程序中实现复杂的几何建模功能。

#include <BRepFill_LocationLaw.hxx>
#include <BRepFill_SectionPlacement.hxx>
#include <TopoDS_Shape.hxx>
#include <gp_Trsf.hxx>
#include <TColgp_HArray1OfPnt.hxx>
#include <Geom_CylindricalSurface.hxx>
#include <GeomAPI_PointsToBSpline.hxx>
#include <Geom_BSplineCurve.hxx>
#include <BRepBuilderAPI_MakeEdge.hxx>
#include <TopoDS_Edge.hxx>
#include <GC_MakeSegment.hxx>
#include <gp_Lin2d.hxx>
#include <GC_MakeArcOfCircle.hxx>
#include <IntAna2d_AnaIntersection.hxx>
#include <BRepBuilderAPI_MakeWire.hxx>
#include <BRepPrimAPI_MakeRevol.hxx>
#include <BRepBuilderAPI_Transform.hxx>
#include <GeomFill_TrihedronLaw.hxx>
#include <GeomFill_Frenet.hxx>
#include <GeomFill_CurveAndTrihedron.hxx>
#include <BRepFill_Edge3DLaw.hxx>
#include"Viewer.h"
TopoDS_Edge createHelix(const Standard_Real HelixRadius, const Standard_Real HelixAngle, const Standard_Real HelixLength)
{
    Standard_Real u0 = 0.0;
    Standard_Real u1 = 2 * M_PI;
    Standard_Real v0 = 0.0;
    Standard_Real v1 = HelixLength;
    double uInter = (u1 - u0) / 1000;
    double vInter = (v1 - v0) / 1000;
    TColgp_HArray1OfPnt Points(1, 1001);
    Handle(Geom_CylindricalSurface) aCylinder = new Geom_CylindricalSurface(gp::XOY(), HelixRadius);
    double u;
    double v;
    //生成点
    for (int i = 0; i < 1001; i++) {
        u = i * vInter * tan(HelixAngle) / HelixRadius;
        v = i * vInter;
        Points[i + 1] = aCylinder->Value(u, v);
    }
    GeomAPI_PointsToBSpline Approx(Points);
    Handle_Geom_BSplineCurve K = Approx.Curve();
    TopoDS_Edge aHelixEdge = BRepBuilderAPI_MakeEdge(K);
    return aHelixEdge;
}

TopoDS_Shape createGrindingwheel2()
{
    Standard_Real Line1_angle = 280 * M_PI / 180;
    Standard_Real Line1_length = 0.5031;
    Standard_Real Line2_angle = 236 * M_PI / 180;
    Standard_Real Line2_length = 0.5925;
    Standard_Real Arc1_r = 0.112;
    Standard_Real Arc1_angle = (180 + 10 + 50) * M_PI / 180;
    gp_Pnt Line1_p1(-0.6822 / 2, 0, 0);
    gp_Pnt Line2_p1(0.6822 / 2, 0, 0);
    gp_Lin Line1(Line1_p1, gp_Dir(cos(Line1_angle), sin(Line1_angle), 0.));
    gp_Lin Line2(Line2_p1, gp_Dir(cos(Line2_angle), sin(Line2_angle), 0.));
    Handle(Geom_TrimmedCurve) L1 = GC_MakeSegment(Line1, 0., Line1_length);
    TopoDS_Edge L1e = BRepBuilderAPI_MakeEdge(L1);
    Handle(Geom_TrimmedCurve) L2 = GC_MakeSegment(Line2, 0., Line2_length);
    TopoDS_Edge L2e = BRepBuilderAPI_MakeEdge(L2);
    gp_Pnt l1end = L1->EndPoint();
    gp_Pnt l2end = L2->EndPoint();
    gp_Lin Line1v(l1end, gp_Dir(cos(Line1_angle + M_PI_2), sin(Line1_angle + M_PI_2), 0.));
    gp_Lin2d Line2v(gp_Pnt2d(l2end.X(), l2end.Y()), gp_Dir2d(cos(Line2_angle - M_PI_2), sin(Line2_angle - M_PI_2)));
    gp_Lin Line2v3d(l2end, gp_Dir(cos(Line2_angle - M_PI_2), sin(Line2_angle - M_PI_2), 0.));
    Handle(Geom_TrimmedCurve) L1v = GC_MakeSegment(Line1v, 0., Arc1_r);
    gp_Pnt l1vend = L1v->EndPoint();
    gp_Circ c1(gp_Ax2(l1vend, gp_Dir(0, 0, 1)), Arc1_r);
    Handle(Geom_TrimmedCurve) c1c = GC_MakeArcOfCircle(c1, l1end, Arc1_angle, 1);
    gp_Pnt c1end = c1c->EndPoint();
    gp_Lin2d Line3(gp_Pnt2d(c1end.X(), c1end.Y()), gp_Dir2d(l2end.X() - c1end.X(), l2end.Y() - c1end.Y()));
    gp_Lin2d Line3v = Line3.Normal(gp_Pnt2d((l2end.X() + c1end.X()) / 2, (l2end.Y() + c1end.Y()) / 2));
    IntAna2d_AnaIntersection aIntAna;
    aIntAna.Perform(Line2v, Line3v);
    IntAna2d_IntPoint aIntPoint = aIntAna.Point(1);
    gp_Pnt o2(aIntPoint.Value().X(), aIntPoint.Value().Y(), 0.);
    Handle(Geom_TrimmedCurve) L2v = GC_MakeSegment(Line2v3d, l2end, o2);
    Standard_Real r2 = L2v->LastParameter();
    gp_Circ c2(gp_Ax2(o2, gp_Dir(0, 0, 1)), r2);
    Handle(Geom_TrimmedCurve) c2c = GC_MakeArcOfCircle(c2, c1end, l2end, 0);
    gp_Pnt c2low = c2c->Value(M_PI_2);

    TopoDS_Edge c1ce = BRepBuilderAPI_MakeEdge(c1c);
    TopoDS_Edge L1ev = BRepBuilderAPI_MakeEdge(L1v);
    TopoDS_Edge c2ce = BRepBuilderAPI_MakeEdge(c2c);

    gp_Pnt Line1_up(-0.9832 / 2, 5, 0);
    gp_Pnt Line2_up(0.9832 / 2, 5, 0);
    TopoDS_Edge anEdge1 = BRepBuilderAPI_MakeEdge(Line1_p1, Line1_up);
    TopoDS_Edge anEdge2 = BRepBuilderAPI_MakeEdge(Line1_up, Line2_up);
    TopoDS_Edge anEdge3 = BRepBuilderAPI_MakeEdge(Line2_up, Line2_p1);
    TopTools_ListOfShape listEdge;
    listEdge.Append(anEdge1);
    listEdge.Append(anEdge2);
    listEdge.Append(anEdge3);
    listEdge.Append(L1e);
    listEdge.Append(c1ce);
    listEdge.Append(c2ce);
    listEdge.Append(L2e);
    BRepBuilderAPI_MakeWire mw;
    mw.Add(listEdge);
    mw.Build();

    TopoDS_Shape gwheel = BRepPrimAPI_MakeRevol(mw, gp_Ax1(gp_Pnt(0, 5, 0), gp_Dir(1, 0, 0)), 2 * M_PI);
    //平移：
    gp_Trsf theTransformation1;
    gp_Vec theVectorOfTranslation1(-c2low.X(), -c2low.Y(), 0.);
    theTransformation1.SetTranslation(theVectorOfTranslation1);

    BRepBuilderAPI_Transform myBRepTransformation1(gwheel, theTransformation1);
    TopoDS_Shape outzero = myBRepTransformation1.Shape();


    gp_Trsf theTransformation2;
    gp_Vec theVectorOfTranslation2(0., 0.525 / 2, 0.);
    theTransformation2.SetTranslation(theVectorOfTranslation2);
    //绕一个轴旋转：
    gp_Trsf theTransformation3;
    gp_Ax1 axez = gp_Ax1(gp_Pnt(0, 0, 0), gp_Dir(0., 0., 1.));
    theTransformation3.SetRotation(axez, -90 * M_PI / 180);

    gp_Trsf theTransformation4;
    gp_Ax1 axex = gp_Ax1(gp_Pnt(0, 0, 0), gp_Dir(1., 0., 0.));
    theTransformation4.SetRotation(axex, -50 * M_PI / 180);

    BRepBuilderAPI_Transform myBRepTransformation(outzero, theTransformation4 * theTransformation3 * theTransformation2);
    TopoDS_Shape TransformedShape = myBRepTransformation.Shape();

    return TransformedShape;
}

int main() {
    // 假设已经有了一个截面形状 sectionShape 和一个路径定律 law
    TopoDS_Shape sectionShape = createGrindingwheel2(); // 这里需要你填入实际的截面形状
    Standard_Real R = 0.306 / 2;
    TopoDS_Edge aE = createHelix(R, M_PI / 4, 6.);
    TopoDS_Wire spine = BRepBuilderAPI_MakeWire(aE);
    Handle(GeomFill_TrihedronLaw) TLaw;
    TLaw = new GeomFill_Frenet();
    Handle(GeomFill_CurveAndTrihedron) Loc = new (GeomFill_CurveAndTrihedron) (TLaw);
    
    Handle(BRepFill_LocationLaw) law; // 这里需要你填入实际的路径定律
    law = new (BRepFill_Edge3DLaw) (spine, Loc);
    // 创建 BRepFill_SectionPlacement 对象进行自动放置
    BRepFill_SectionPlacement placement(
        law, sectionShape, Standard_False, Standard_False);

    // 获取放置操作产生的变换矩阵
    gp_Trsf transformation = placement.Transformation();

    // 打印变换矩阵（或者进行其他操作）
    std::cout << "Transformation matrix:" << std::endl;
    for (Standard_Integer i = 1; i <= 3; ++i) {
        for (Standard_Integer j = 1; j <= 4; ++j) {
            std::cout << transformation.Value(i, j) << " ";
        }
        std::cout << std::endl;
    }

    // 获取截面在路径上的曲线坐标
    Standard_Real abscissa = placement.AbscissaOnPath();
    std::cout << "Abscissa on path: " << abscissa << std::endl;
    TopoDS_Shape ch = BRepBuilderAPI_Transform(sectionShape, transformation, Standard_True);

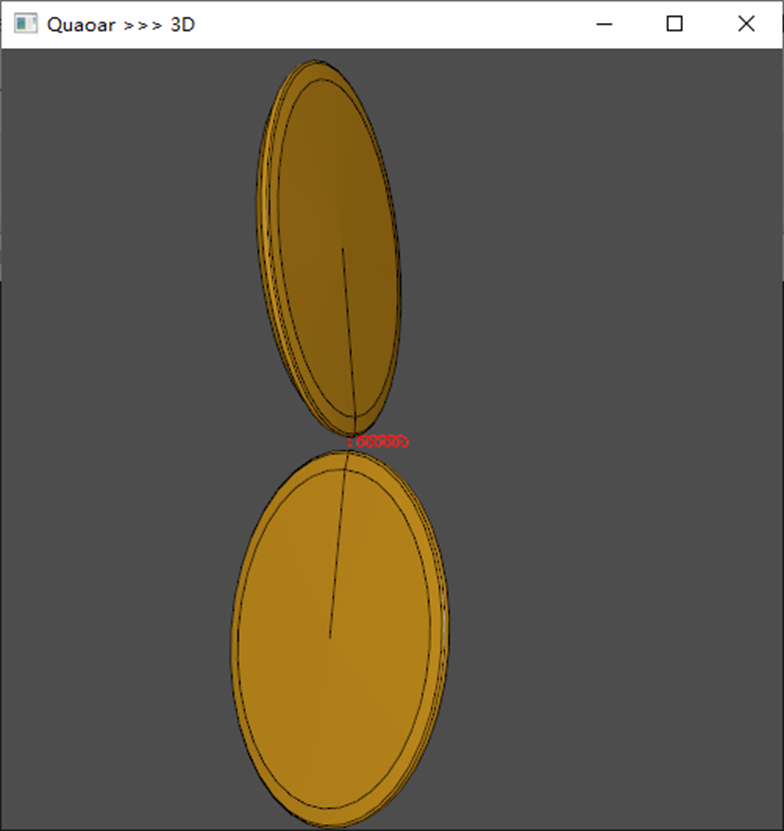
    Viewer vout(50, 50, 500, 500);
    vout << sectionShape;
    vout << spine;
    vout << ch;

    vout.StartMessageLoop();
    return 0;
}

Transformation matrix:

-0.985547 -0.133209 0.104656 0.150789

0.167884 -0.685475 0.708476 -0.0256862

-0.0226364 0.715806 0.697932 0.00346336

Abscissa on path: 0