SVD奇异值分解原理及应用

--------------------------------------------------------------------------------------------------------------------------------

首先说明：本文的内容来自百家号“人工智能遇见磐创”大佬的整理，感谢原作者（本文在原作者的基础上按照自己的理解进行了修改，整合。如有不妥，请联系删除）。

原文地址：百度安全验证https://baijiahao.baidu.com/s?id=1643076332887222975&wfr=spider&for=pchttps://baijiahao.baidu.com/s?id=1643076332887222975&wfr=spider&for=pc

--------------------------------------------------------------------------------------------------------------------------------

大家发现没有？我们大学学过的线性代数在现实世界中基本没用。

好吧，但我可以向你保证，并不是这样的。特别是如果你想开启数据科学的职业生涯，那我们就开始吧，保证不让您失望。

线性代数弥合了理论与概念实际实施之间的差距。对线性代数的掌握理解打开了我们认为无法理解的机器学习算法的大门。

线性代数的一种这样的用途是奇异值分解(SVD)用于降维。

你在数据科学中一定很多次遇到SVD。它无处不在，特别是当我们处理降维时。但它是什么？它是如何工作的？SVD应用有什么？

事实上，SVD是推荐系统的基础，而推荐系统是谷歌，YouTube，亚马逊，Facebook等大公司的核心。

接下来，我们一起看看这个奇怪而陌生的东西：SVD。

1、SVD分解原理

通过关于SVD及其应用的所有文献，你将非常频繁地遇到术语“矩阵的秩”。那么让我们从了解这是什么开始。

1.1 矩阵的秩

矩阵的秩是矩阵中线性无关的行(或列)向量的最大数量。如果向量r不能表示为r1和r2的线性组合，则称向量r与向量r1和r2线性无关。

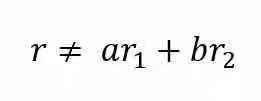
考虑下面的三个矩阵：

（1）在矩阵A中，行向量r2是r1的倍数，r2 = 2 r1，因此它只有一个无关的行向量。Rank(A)= 1

（2）在矩阵B中，行向量r3是r1和r2之和，r3 = r1 + r2，但r1和r2是无关的，Rank(B)= 2

（3）在矩阵C中，所有3行彼此无关。Rank(C)= 3

矩阵的秩可以被认为是由矩阵表示的独特信息量（也就是不相关的信息量）多少的代表。秩越高，信息越高。

1.2 SVD

SVD将矩阵分解为3个矩阵的乘积，如下所示：

如果A是m x n矩阵：

U是左奇异向量的m×m矩阵
S是以递减顺序排列的奇异值的m×n对角矩阵
V是右奇异向量的n×n矩阵

1.3 为什么SVD用于降维？

你可能想知道我们为什么要经历这种看似辛苦的分解。可以通过分解的替代表示来理解原因。见下图：

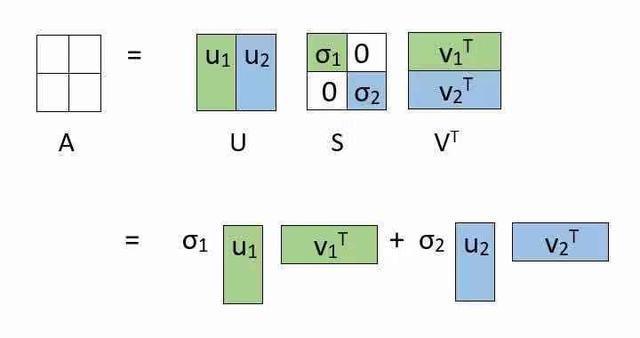
分解允许我们将原始矩阵表示为低秩矩阵的线性组合（也就是说，复杂的矩阵A可以用 $\sigma_1$ 和 $\sigma_2$ 两个参数表示，是不是就降低维度了？从2维数组降低到1维向量了？）。

在实际应用中，你将观察到的只有前几个(比如k)奇异值很大，其余的奇异值接近于零。因此，可以忽略除前几个之外而不会丢失大量信息。请参见下图中的矩阵截断方式：

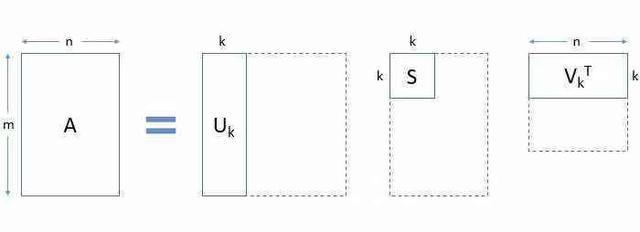
也就是说A可以由前k个参数的线性组合近似表示，近似程度能达到90%。

总结以下3点：

使用SVD，我们能够用3个较小的矩阵U，S和V表示我们的大矩阵A
这在大型计算中很有用，如一张超像素照片4560*2780，这张照片可能有20M，但是我们可以仅使用100个 $\sigma$ 表示即可，100个 $\sigma$ 的存储空间也就是几K。
我们可以得到A的k-秩近似。为此，选择前k个奇异值并相应地截断3个矩阵。

2、SVD分解应用

SVD是将矩阵A分解为3个矩阵（U，S和V）。S是奇异值的对角矩阵。将奇异值视为矩阵中不同特征的重要性值矩阵的秩是对存储在矩阵中的独特信息的度量。秩越高，信息越多矩阵的特征向量是数据的最大扩展或方差的方向在大多数应用中，我们希望将高秩矩阵缩减为低秩矩阵，同时保留重要信息。

我们将在此处遵循自上而下的方法并首先讨论SVD应用。现在你只需要知道四点来理解这些应用：

图片压缩：在图像处理中，SVD分解常被用于图像压缩。通过对图像矩阵进行SVD分解，可以得到较低秩的近似矩阵，从而减少存储空间和传输带宽。这种方法在JPEG2000等图像压缩算法中得到广泛应用。
SLAM: 对极几何分解本质矩阵求R，t
推荐系统：SVD分解在推荐系统中也有重要的应用。通过对用户评分矩阵进行SVD分解，可以将用户和物品映射到一个隐空间中，并预测用户对未评分物品的喜好程度。基于SVD的协同过滤算法在Netflix Prize竞赛中取得了很大成功。
数据降维：SVD分解可以将高维数据降维到低维，保留数据的主要特征。这在机器学习和数据挖掘任务中非常有用，可以提高计算效率并减少存储需求。例如，在主成分分析（PCA）中，SVD分解被广泛用于实现数据降维。

2.1 SVD用于图像压缩

# 下载图片 "https://cdn.pixabay.com/photo/2017/03/27/16/50/beach-2179624_960_720.jpg"
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import cv2
# 灰度化读取图片
img = cv2.imread('beach-2179624_960_720.jpg', 0)

plt.imshow(img)
plt.axis('off')  # 关闭坐标轴
plt.show()

# 得到svd
U, S, V = np.linalg.svd(img)
# 得到矩阵的形状
print(U.shape, S.shape, V.shape)
# 以不同component数绘制图像
comps = [638, 500, 400, 300, 200, 100]
plt.figure(figsize = (16, 8))
for i in range(6):
    low_rank = U[:, :comps[i]] @ np.diag(S[:comps[i]]) @ V[:comps[i], :]
    if(i == 0):
        plt.subplot(2, 3, i+1), plt.imshow(low_rank, cmap = 'gray'), plt.axis('off'), plt.title("Original Image with n_components =" + str(comps[i]))

    else:
        plt.subplot(2, 3, i+1), plt.imshow(low_rank, cmap = 'gray'), plt.axis('off'), plt.title("n_components =" + str(comps[i]))

plt.show()

2.2 SVD用于图像恢复

图像恢复其实就是通过矩阵填充来实现。

矩阵填充是在部分观察的矩阵中填充缺失元素的过程。Netflix问题就是一个常见的例子。

给定一个评级矩阵，其中每个元素(i，j)表示客户i对电影j的评级，即客户i观看了电影j，否则该值为缺失值，我们想要预测剩余的元素以便对客户于提出好的建议。

在图像矩阵中！由于图像是连续的，大多数像素的值取决于它们周围的像素。因此，低秩矩阵可以是这些图像的良好近似。

图片来自：Chen, Zihan. “Singular Value Decomposition and its Applications in Image Processing.” ACM, 2018

2.3 SVD用于特征脸

论文“Eigenfaces for Recognition”于1991年发表。在此之前，大多数面部识别方法都涉及识别个体特征，如眼睛或鼻子，并根据这些特征之间的位置，大小和关系来开发模型。

特征脸方法试图在面部图像中提取相关信息，尽可能有效地对其进行编码，并将一个面部编码与数据库中的模型编码进行比较。

通过将每个面部表达为新面部空间中所选择的特征脸的线性组合来获得编码。

把这个方法分解为五个步骤：

收集面部训练集
通过找到最大方差的方向-特征向量或特征脸来找到最重要的特征
选择对应于最高特征值的M个特征脸（这些特征脸现在定义了一个新的面部空间）
将所有数据投影到此面部空间中
对于新面部，将其投影到新面部空间中，找到空间中最近的面部，并将面部分类为已知或未知面部

可以使用PCA和SVD找到这些特征脸。这是我在Labeled Faces in the Wild数据集中上执行SVD后获得的几个特征脸中的第一个：

我们可以看到，只有前几行中的图像看起来像实际的面部。其他看起来很糟糕，因此我放弃了它们。我保留了总共120个特征脸，并将数据转换为新的面部空间。然后我使用k近邻分类器来预测基于面部的姓名。

你可以在下面看到分类报告。显然，还有改进的余地。你可以尝试调整特征脸的数量或使用不同的分类器进行试验：

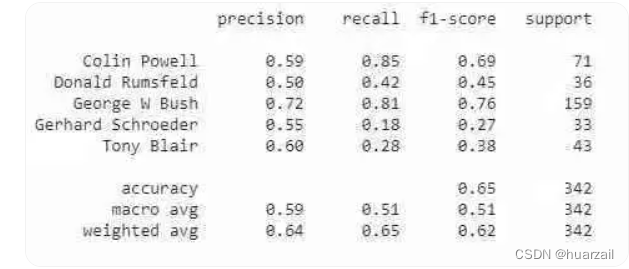
看看一些预测值及其真实标签：

2.4 SVD用于谱聚类

聚类是将类似对象划分在一起的任务。这是一种无监督的机器学习技术。对于我们大多数人来说，聚类是K-Means聚类(一种简单但功能强大的算法)的代名词,但是，这并不是准确的说法。

考虑以下情况：

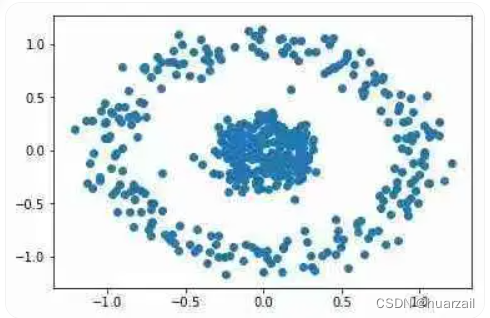
显然，同心圆中有2个簇。但是，n_clusters = 2的KMeans给出了以下簇：

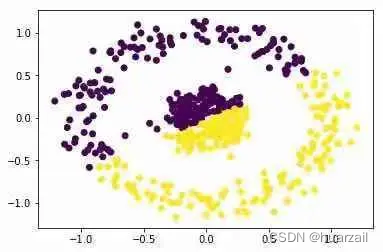
K-Means绝对不是这里使用的合适算法。谱聚类是一种可以解决这个问题的技术，它源于图论。以下是基本步骤：

从数据Affnity matrix(A)或Adjacent matrix开始。这表示一个对象与另一个对象的相似程度。在图中，这将表示点之间是否存在边缘
找到每个对象的 Degree matrix (D) 。这是一个对角矩阵，其元素(i，i)等于对象i相似的对象数
找到Affnity matrix的 Laplacian matrix(L) (L)：L = A - D
根据它们的特征值找到Laplacian matrix的最高k个特征向量
在这些特征向量上运行k-means，将对象聚类为k类

你可以通过下面的链接阅读完整的算法及其数学原理^2,而scikit-learn中谱聚类的实现类似于KMeans：

from sklearn.datasets import make_circles
from sklearn.neighbors import kneighbors_graph
from sklearn.cluster import SpectralClustering
import numpy as np
import matplotlib.pyplot as plt
# s生成数据
X, labels = make_circles(n_samples=500, noise=0.1, factor=.2)
# 可视化数据
plt.scatter(X[:, 0], X[:, 1])
plt.show()
# 训练和预测
s_cluster = SpectralClustering(n_clusters = 2, eigen_solver='arpack',
affinity="nearest_neighbors").fit_predict(X)
# 可视化结果
plt.scatter(X[:, 0], X[:, 1], c = s_cluster)
plt.show()

你将从上面的代码中得到以下不错的聚类结果：

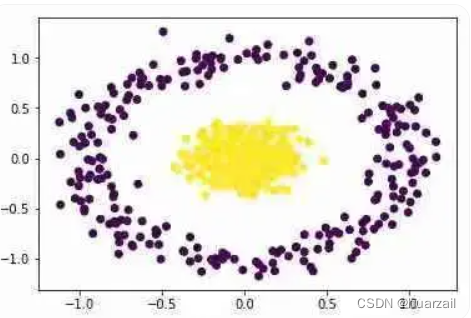
2.5 SVD用于从视频中删除背景

想一想如何区分视频背景和前景。视频的背景基本上是静态的 - 它看不到很多变化。所有的变化都在前景中看到。这是我们用来将背景与前景分开的属性。

以下是我们可以采用的步骤来实现此方法：

从视频创建矩阵M -- 这是通过定期从视频中采样图像快照，将这些图像矩阵展平为数组，并将它们存储为矩阵M的列。我们得到以下矩阵M的图：

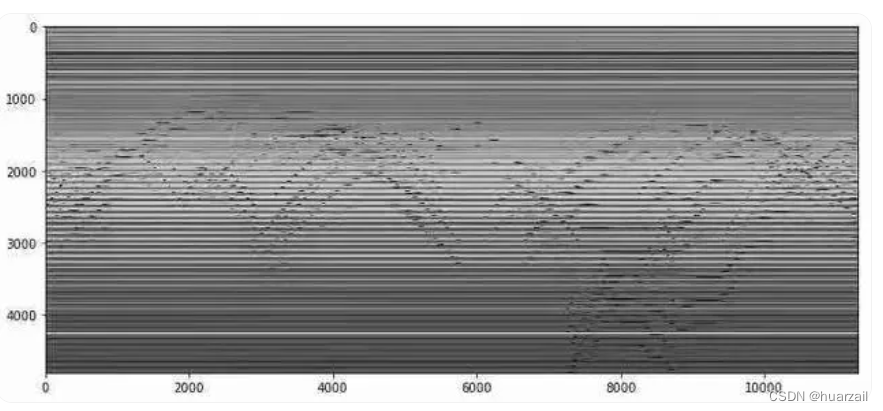
你认为这些水平和波浪线代表什么？花一点时间考虑一下。

水平线表示在整个视频中不改变的像素值。基本上，这些代表了视频中的背景。波浪线显示变化并代表前景。

因此，我们可以将M视为两个矩阵的总和 - 一个表示背景，另一个表示前景
背景矩阵没有看到像素的变化，因此是多余的，即它没有很多独特的信息。所以，它是一个低秩矩阵
因此，M的低秩近似是背景矩阵。我们在此步骤中使用SVD
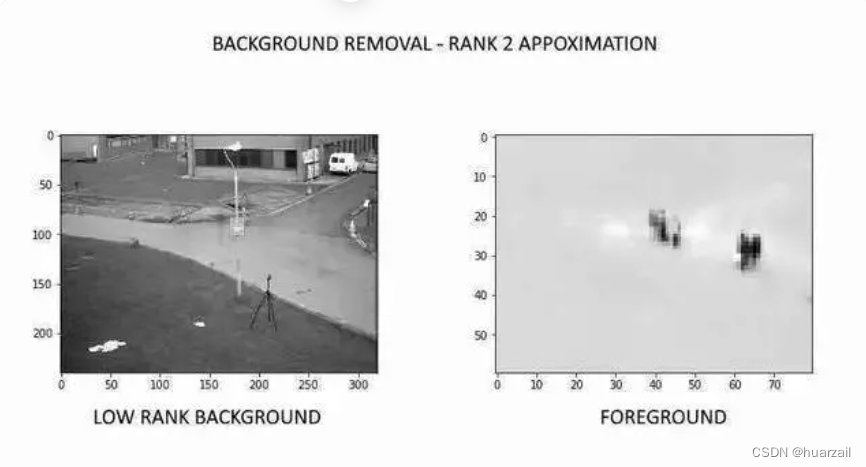
我们可以通过简单地从矩阵M中减去背景矩阵来获得前景矩阵
这是视频一个删除背景后的帧：

3. 3种在Python中使用SVD的方法

我们知道什么是SVD，它是如何工作的，以及它在现实世界中的用途。但是我们如何自己实现SVD呢？

SVD的概念听起来很复杂。你可能想知道如何找到3个矩阵U，S和V。如果我们手动计算这些矩阵，这是一个漫长的过程。

幸运的是，我们不需要手动执行这些计算。我们可以用三种简单的方式在Python中实现SVD。

3.1 numpy中的SVD

NumPy是Python中科学计算的基础包。它具有有用的线性代数功能以及其他应用。

你可以使用numpy.linalg中的SVD获取完整的矩阵U，S和V。注意，S是对角矩阵，这意味着它的大多数元素都是0。这称为稀疏矩阵。为了节省空间，S作为奇异值的一维数组而不是完整的二维矩阵返回。

import numpy as np
from numpy.linalg import svd
# 定义二维矩阵
A = np.array([[4, 0], [3, -5]])
U, S, VT = svd(A)
print("Left Singular Vectors:")
print(U)
print("Singular Values:")
print(np.diag(S))
print("Right Singular Vectors:")
print(VT)
# 检查分解是否正确
# @ 表示矩阵乘法
print(U @ np.diag(S) @ VT)

3.2 scikit-learn中的Truncated SVD

在大多数常见的应用中，我们不希望找到完整的矩阵U，S和V。我们在降维和潜在语义分析中看到了这一点，还记得吗？

我们最终会修剪矩阵，所以为什么要首先找到完整的矩阵？

在这种情况下，最好使用sklearn.decomposition中的TruncatedSVD。你可以通过n_components参数指定所需的特征数量输出。n_components应严格小于输入矩阵中的特征数：

import numpy as np
from sklearn.decomposition import TruncatedSVD
A = np.array([[-1, 2, 0], [2, 0, -2], [0, -2, 1]])
print("Original Matrix:")
print(A)
svd = TruncatedSVD(n_components = 2)
A_transf = svd.fit_transform(A)
print("Singular values:")
print(svd.singular_values_)
print("Transformed Matrix after reducing to 2 features:")
print(A_transf)

3.3 scikit-learn中的Randomized SVD

Randomized SVD提供与Truncated SVD相同的结果，并且具有更快的计算时间。Truncated SVD使用ARPACK精确求解，但随机SVD使用了近似技术。

import numpy as np
from sklearn.utils.extmath import randomized_svd
A = np.array([[-1, 2, 0], [2, 0, -2], [0, -2, 1]])
u, s, vt = randomized_svd(A, n_components = 2)
print("Left Singular Vectors:")
print(u)
print("Singular Values:")
print(np.diag(s))
print("Right Singular Vectors:")
print(vt)

参考文献：

百度安全验证https://baijiahao.baidu.com/s?id=1643076332887222975&wfr=spider&for=pc