机器学习笔记之深度信念网络——贪心逐层预训练算法
- 引言
- 回顾:深度信念网络的结构表示
- 回顾: RBM \text{RBM} RBM叠加思想
- 贪心逐层预训练算法
引言
上一节介绍了深度信念网络模型的构建思想,本节将介绍后验概率求解——贪心逐层预训练算法。
回顾:深度信念网络的结构表示
深度信念网络本质上是 在已有
Sigmoid
\text{Sigmoid}
Sigmoid信念网络的基础上,使用
RBM
\text{RBM}
RBM层对隐变量的边缘概率分布进行学习 的逻辑。已知一个深度信念网络表示如下:
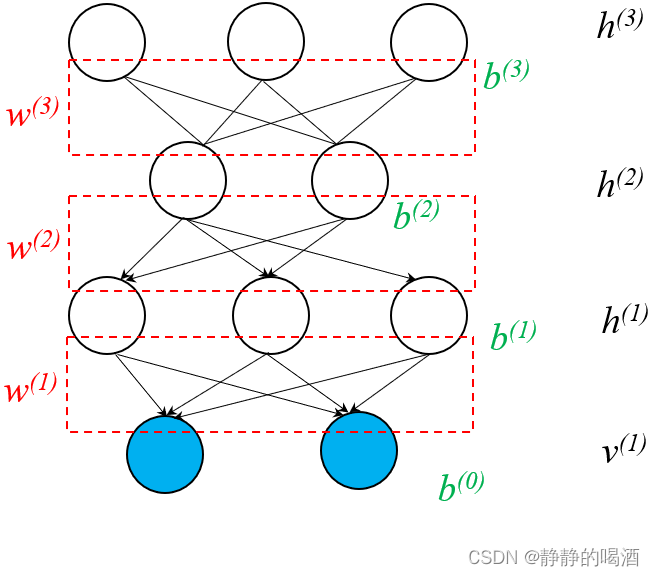
这明显是一个四层深度信念网络,具体包含两个部分:
- 观测变量层 v ( 1 ) v^{(1)} v(1),隐变量层 h ( 1 ) , h ( 2 ) h^{(1)},h^{(2)} h(1),h(2)组成的 Sigmoid \text{Sigmoid} Sigmoid信念网络;
- 隐变量层 h ( 1 ) , h ( 2 ) h^{(1)},h^{(2)} h(1),h(2)组成的受限玻尔兹曼机
该网络中随机变量结点的联合概率分布可表示为:
任意相邻的随机变量层之间存在关联关系,也就是说,没有直接关联关系的层如
h
(
1
)
h^{(1)}
h(1)与
h
(
3
)
h^{(3)}
h(3)之间条件独立。具体结构详见:贝叶斯网络——结构表示与马尔可夫随机场——结构表示
P
(
v
(
1
)
,
h
(
1
)
,
h
(
2
)
,
h
(
3
)
)
=
P
(
v
(
1
)
∣
h
(
1
)
,
h
(
2
)
,
h
(
3
)
)
⋅
P
(
h
(
1
)
,
h
(
2
)
,
h
(
3
)
)
=
P
(
v
(
1
)
∣
h
(
1
)
)
⋅
P
(
h
(
1
)
∣
h
(
2
)
,
h
(
3
)
)
⋅
P
(
h
(
2
)
,
h
(
3
)
)
=
P
(
v
(
1
)
∣
h
(
1
)
)
⋅
P
(
h
(
1
)
∣
h
(
2
)
)
⋅
P
(
h
(
2
)
,
h
(
3
)
)
\begin{aligned} \mathcal P(v^{(1)},h^{(1)},h^{(2)},h^{(3)}) & = \mathcal P(v^{(1)} \mid h^{(1)},h^{(2)},h^{(3)}) \cdot \mathcal P(h^{(1)},h^{(2)},h^{(3)}) \\ & = \mathcal P(v^{(1)} \mid h^{(1)}) \cdot \mathcal P(h^{(1)} \mid h^{(2)},h^{(3)}) \cdot \mathcal P(h^{(2)},h^{(3)}) \\ & = \mathcal P(v^{(1)} \mid h^{(1)}) \cdot \mathcal P(h^{(1)} \mid h^{(2)}) \cdot \mathcal P(h^{(2)},h^{(3)}) \end{aligned}
P(v(1),h(1),h(2),h(3))=P(v(1)∣h(1),h(2),h(3))⋅P(h(1),h(2),h(3))=P(v(1)∣h(1))⋅P(h(1)∣h(2),h(3))⋅P(h(2),h(3))=P(v(1)∣h(1))⋅P(h(1)∣h(2))⋅P(h(2),h(3))
其中,
P
(
v
(
1
)
∣
h
(
1
)
)
,
P
(
h
(
1
)
∣
h
(
2
)
)
\mathcal P(v^{(1)} \mid h^{(1)}),\mathcal P(h^{(1)} \mid h^{(2)})
P(v(1)∣h(1)),P(h(1)∣h(2))均是
Sigmoid
\text{Sigmoid}
Sigmoid信念网络关于随机变量的后验概率,因而可以进行如下表示:
其中
W
h
(
1
)
→
v
(
1
)
,
W
h
(
2
)
→
h
(
1
)
\mathcal W_{h^{(1)} \to v^{(1)}},\mathcal W_{h^{(2)} \to h^{(1)}}
Wh(1)→v(1),Wh(2)→h(1)均表示随机变量层与层之间的权重信息,并且均以矩阵的方式表示,例如:
W
h
(
1
)
→
v
(
1
)
=
[
W
h
j
(
1
)
→
v
i
(
1
)
]
∣
D
∣
×
∣
P
(
1
)
∣
\mathcal W_{h^{(1)} \to v^{(1)}} = \left[\mathcal W_{h_j^{(1)} \to v_i^{(1)}}\right]_{|\mathcal D| \times |\mathcal P^{(1)}|}
Wh(1)→v(1)=[Whj(1)→vi(1)]∣D∣×∣P(1)∣
其中
D
,
P
(
1
)
\mathcal D,\mathcal P^{(1)}
D,P(1)分别表示观测变量层、第一层隐变量的随机变量集合;对应的
∣
D
∣
,
∣
P
(
1
)
∣
|\mathcal D|,|\mathcal P^{(1)}|
∣D∣,∣P(1)∣表示各层随机变量的个数。
同理,对应层的偏置项
b
(
k
)
(
k
=
0
,
1
,
2
,
3
)
b^{(k)}(k=0,1,2,3)
b(k)(k=0,1,2,3)表示为(以
b
(
0
)
b^{(0)}
b(0)为例):
b
(
0
)
=
(
b
1
(
0
)
,
b
2
(
0
)
,
⋯
,
b
∣
D
∣
(
0
)
)
∣
D
∣
×
1
T
b^{(0)} = \left(b_1^{(0)},b_2^{(0)},\cdots,b_{|\mathcal D|}^{(0)}\right)_{|\mathcal D| \times 1}^T
b(0)=(b1(0),b2(0),⋯,b∣D∣(0))∣D∣×1T
两种后验概率均表示生成过程,详见Sigmoid信念网络的定义。
P
(
v
(
1
)
∣
h
(
1
)
)
=
Sigmoid
{
[
W
h
(
1
)
→
v
(
1
)
]
T
h
(
1
)
+
b
(
0
)
}
P
(
h
(
1
)
∣
h
(
2
)
)
=
Sigmoid
{
[
W
h
(
2
)
→
h
(
1
)
]
T
h
(
2
)
+
b
(
1
)
}
\begin{aligned} \mathcal P(v^{(1)} \mid h^{(1)}) = \text{Sigmoid} \left\{\left[\mathcal W_{h^{(1)} \to v^{(1)}}\right]^T h^{(1)} + b^{(0)}\right\} \\ \mathcal P(h^{(1)} \mid h^{(2)}) = \text{Sigmoid} \left\{ \left[\mathcal W_{h^{(2)} \to h^{(1)}}\right]^T h^{(2)} + b^{(1)}\right\} \end{aligned}
P(v(1)∣h(1))=Sigmoid{[Wh(1)→v(1)]Th(1)+b(0)}P(h(1)∣h(2))=Sigmoid{[Wh(2)→h(1)]Th(2)+b(1)}
关于
P
(
h
(
2
)
,
h
(
3
)
)
\mathcal P(h^{(2)},h^{(3)})
P(h(2),h(3))表示受限玻尔兹曼机的联合概率分布(概率密度函数)。根据受限玻尔兹曼机的模型表示可表示为:
其中
Z
\mathcal Z
Z表示配分函数。需要注意的是’受限玻尔兹曼机‘的权重参数不包含结点之间的因果关系,因此这里使用
W
h
(
2
)
⇔
h
(
3
)
\mathcal W_{h^{(2)} \Leftrightarrow h^{(3)}}
Wh(2)⇔h(3)进行表示。
P
(
h
(
2
)
,
h
(
3
)
)
=
1
Z
{
[
h
(
3
)
]
T
W
h
(
2
)
⇔
h
(
3
)
⋅
h
(
3
)
+
[
b
(
2
)
]
T
h
(
2
)
+
[
b
(
3
)
]
T
h
(
3
)
}
\mathcal P(h^{(2)},h^{(3)}) = \frac{1}{\mathcal Z} \left\{ \left[h^{(3)}\right]^T \mathcal W_{h^{(2)} \Leftrightarrow h^{(3)}} \cdot h^{(3)} + \left[b^{(2)}\right]^T h^{(2)} + \left[b^{(3)}\right]^T h^{(3)}\right\}
P(h(2),h(3))=Z1{[h(3)]TWh(2)⇔h(3)⋅h(3)+[b(2)]Th(2)+[b(3)]Th(3)}
回顾: RBM \text{RBM} RBM叠加思想
如果针对一个
Sigmoid
\text{Sigmoid}
Sigmoid信念网络使用极大似然估计求解其模型参数,它的对数似然函数
log
P
(
v
)
\log \mathcal P(v)
logP(v)与证据下界(Evidence of Lower Bound,ELBO)之间的关系表示如下:
由于log函数是’凹函数‘,根据杰森不等式,存在如下表示结果。
log
P
(
v
)
=
log
{
E
Q
(
h
(
1
)
∣
v
)
[
P
(
v
,
h
(
1
)
)
Q
(
h
(
1
)
∣
v
)
]
}
≥
E
Q
(
h
(
1
)
∣
v
)
{
log
[
P
(
v
,
h
(
1
)
)
Q
(
h
(
1
)
∣
v
)
]
}
=
ELBO
=
∑
h
(
1
)
Q
(
h
(
1
)
∣
v
)
[
log
P
(
v
,
h
(
1
)
)
−
log
Q
(
h
(
1
)
∣
v
)
]
=
∑
h
(
1
)
Q
(
h
(
1
)
∣
v
)
[
log
P
(
h
(
1
)
)
+
log
P
(
v
∣
h
(
1
)
)
−
log
Q
(
h
(
1
)
∣
v
)
]
\begin{aligned} \log \mathcal P(v) & = \log \left\{\mathbb E_{\mathcal Q(h^{(1)} \mid v)} \left[\frac{\mathcal P(v,h^{(1)})}{\mathcal Q(h^{(1)} \mid v)}\right]\right\} \\ & \geq \mathbb E_{\mathcal Q(h^{(1)} \mid v)} \left\{\log \left[\frac{\mathcal P(v,h^{(1)})}{\mathcal Q(h^{(1)} \mid v)}\right] \right\} \\ & = \text{ELBO} \\ & = \sum_{h^{(1)}} \mathcal Q(h^{(1)} \mid v) \left[\log \mathcal P(v,h^{(1)}) - \log \mathcal Q(h^{(1)} \mid v)\right] \\ & = \sum_{h^{(1)}} \mathcal Q(h^{(1)} \mid v) \left[\log \mathcal P(h^{(1)}) + \log \mathcal P(v \mid h^{(1)}) - \log \mathcal Q(h^{(1)} \mid v)\right] \end{aligned}
logP(v)=log{EQ(h(1)∣v)[Q(h(1)∣v)P(v,h(1))]}≥EQ(h(1)∣v){log[Q(h(1)∣v)P(v,h(1))]}=ELBO=h(1)∑Q(h(1)∣v)[logP(v,h(1))−logQ(h(1)∣v)]=h(1)∑Q(h(1)∣v)[logP(h(1))+logP(v∣h(1))−logQ(h(1)∣v)]
叠加
RBM
\text{RBM}
RBM本质上是针对隐变量的边缘概率分布
P
(
h
(
1
)
)
\mathcal P(h^{(1)})
P(h(1))。相比于
Sigmoid
\text{Sigmoid}
Sigmoid信念网络自身对
P
(
h
(
1
)
)
\mathcal P(h^{(1)})
P(h(1))结果的计算:
v
(
i
)
v^{(i)}
v(i)是样本集合
V
\mathcal V
V中的具体样本,且各样本独立同分布;
v
i
v_i
vi是观测变量的维度信息,根据
Sigmoid
\text{Sigmoid}
Sigmoid信念网络的结构,观测变量各维度之间条件独立(同父结构)。
P
(
v
)
=
∑
h
(
1
)
P
(
h
(
1
)
)
⋅
P
(
v
∣
h
(
1
)
)
{
P
(
v
)
=
∏
v
(
i
)
∈
V
P
(
v
(
i
)
)
P
(
v
∣
h
(
1
)
)
=
∏
i
=
1
∣
D
∣
P
(
v
i
∣
h
(
1
)
)
P
(
v
i
∣
h
(
1
)
)
=
Sigmoid
(
∑
j
=
1
m
w
i
j
⋅
h
j
+
b
i
)
\begin{aligned} & \mathcal P(v) = \sum_{h^{(1)}} \mathcal P(h^{(1)}) \cdot \mathcal P(v \mid h^{(1)}) \\ & \begin{cases} \mathcal P(v) = \prod_{v^{(i)} \in \mathcal V} \mathcal P(v^{(i)}) \\ \mathcal P(v \mid h^{(1)}) = \prod_{i=1}^{|\mathcal D|} \mathcal P(v_i \mid h^{(1)}) \end{cases} \\ & \mathcal P(v_i \mid h^{(1)}) = \text{Sigmoid} \left(\sum_{j=1}^m w_{ij} \cdot h_j + b_i\right) \end{aligned}
P(v)=h(1)∑P(h(1))⋅P(v∣h(1)){P(v)=∏v(i)∈VP(v(i))P(v∣h(1))=∏i=1∣D∣P(vi∣h(1))P(vi∣h(1))=Sigmoid(j=1∑mwij⋅hj+bi)
将
P
(
v
)
,
P
(
v
∣
h
(
1
)
)
\mathcal P(v),\mathcal P(v \mid h^{(1)})
P(v),P(v∣h(1))代入
P
(
v
)
=
∑
h
(
1
)
P
(
h
(
1
)
)
⋅
P
(
v
∣
h
(
1
)
)
\mathcal P(v) = \sum_{h^{(1)}} \mathcal P(h^{(1)}) \cdot \mathcal P(v \mid h^{(1)})
P(v)=∑h(1)P(h(1))⋅P(v∣h(1))中,我们可以通过模型参数对
P
(
h
(
1
)
)
\mathcal P(h^{(1)})
P(h(1))进行表示。这意味着 梯度上升法对模型参数的不断精进,对于
P
(
h
(
1
)
)
\mathcal P(h^{(1)})
P(h(1))的表示也会越来越准确。
但是这种方法的缺陷在于:即便
P
(
h
(
1
)
)
\mathcal P(h^{(1)})
P(h(1))被表示的越来越准确,但它并没有理论背书。也就是说,每一次迭代
P
(
h
(
1
)
)
\mathcal P(h^{(1)})
P(h(1))均向最优值的方向靠近,但每次迭代可能并没有达到当前迭代步骤的最优解。
而
RBM
\text{RBM}
RBM叠加思想就是给
P
(
h
(
1
)
)
\mathcal P(h^{(1)})
P(h(1))添加了理论基础,使得每次迭代过程中的
P
(
h
(
1
)
)
\mathcal P(h^{(1)})
P(h(1))均是当前迭代步骤理论上的最优值。
而这个理论基础就是针对
P
(
h
(
1
)
)
\mathcal P(h^{(1)})
P(h(1))使用极大似然估计,通过关于
h
(
1
)
h^{(1)}
h(1)层新构建的隐变量使对数似然函数
log
P
(
h
(
1
)
)
\log \mathcal P(h^{(1)})
logP(h(1))达到最大:
{
ϕ
^
=
arg
max
ϕ
log
P
(
h
(
1
)
;
ϕ
)
ϕ
^
⇒
max
P
(
h
(
1
)
)
max
P
(
h
(
1
)
)
⇒
max
ELBO
⇒
log
P
(
v
)
⇑
\begin{cases} \hat \phi = \mathop{\arg\max}\limits_{\phi} \log \mathcal P(h^{(1)};\phi) \\ \hat \phi \Rightarrow \max \mathcal P(h^{(1)}) \\ \max \mathcal P(h^{(1)}) \Rightarrow \max \text{ELBO} \Rightarrow \log \mathcal P(v) \Uparrow \end{cases}
⎩
⎨
⎧ϕ^=ϕargmaxlogP(h(1);ϕ)ϕ^⇒maxP(h(1))maxP(h(1))⇒maxELBO⇒logP(v)⇑
最终,这种方式在每次迭代过程中,使对数似然函数
log
P
(
v
)
\log \mathcal P(v)
logP(v)有一个提升。从而使模型学习更加准确。同理,为了精进
P
(
h
(
1
)
)
\mathcal P(h^{(1)})
P(h(1)),同样可以添加若干层,而不仅仅是一层。
贪心逐层预训练算法
重新观察
ELBO
\text{ELBO}
ELBO的式子:
log
P
(
v
)
≥
ELBO
=
∑
h
(
1
)
Q
(
h
(
1
)
∣
v
)
log
[
P
(
h
(
1
)
)
⋅
P
(
v
∣
h
(
1
)
)
]
−
∑
h
(
1
)
Q
(
h
(
1
)
∣
v
)
log
Q
(
h
(
1
)
∣
v
)
\begin{aligned} \log \mathcal P(v) & \geq \text{ELBO} \\ & = \sum_{h^{(1)}} \mathcal Q(h^{(1)} \mid v) \log \left[\mathcal P(h^{(1)}) \cdot \mathcal P(v \mid h^{(1)}) \right] - \sum_{h^{(1)}} \mathcal Q(h^{(1)} \mid v) \log \mathcal Q(h^{(1)} \mid v) \end{aligned}
logP(v)≥ELBO=h(1)∑Q(h(1)∣v)log[P(h(1))⋅P(v∣h(1))]−h(1)∑Q(h(1)∣v)logQ(h(1)∣v)
在变分推断一节中介绍过:
log
P
(
v
)
=
ELBO
+
KL
[
Q
(
h
(
1
)
∣
v
)
∣
∣
P
(
h
(
1
)
∣
v
)
]
\log \mathcal P(v) = \text{ELBO} + \text{KL}[\mathcal Q(h^{(1)} \mid v) || \mathcal P(h^{(1)} \mid v)]
logP(v)=ELBO+KL[Q(h(1)∣v)∣∣P(h(1)∣v)]
其中
KL
[
Q
(
h
(
1
)
∣
v
)
∣
∣
P
(
h
(
1
)
∣
v
)
]
\text{KL}[\mathcal Q(h^{(1)} \mid v) || \mathcal P(h^{(1)} \mid v)]
KL[Q(h(1)∣v)∣∣P(h(1)∣v)]表示假设分布
Q
(
h
(
1
)
∣
v
)
\mathcal Q(h^{(1)} \mid v)
Q(h(1)∣v)与真实分布
P
(
h
(
1
)
∣
v
)
\mathcal P(h^{(1)} \mid v)
P(h(1)∣v)之间相似关系的
KL
\text{KL}
KL散度。当
Q
(
h
(
1
)
∣
v
)
=
P
(
h
(
1
)
∣
v
)
\mathcal Q(h^{(1)} \mid v) = \mathcal P(h^{(1)} \mid v)
Q(h(1)∣v)=P(h(1)∣v),此时有:
log
P
(
v
)
=
ELBO
\log \mathcal P(v) = \text{ELBO}
logP(v)=ELBO。
如果仅仅是受限玻尔兹曼机(没有添加任何其他隐变量层),
P
(
h
(
1
)
∣
v
)
\mathcal P(h^{(1)} \mid v)
P(h(1)∣v)是可以直接求解的:
关于受限玻尔兹曼机后验分布
P
(
h
∣
v
)
\mathcal P(h \mid v)
P(h∣v)求解详见:受限玻尔兹曼机-推断任务-后验概率
之所以能够求解的原因在于:给定观测变量条件下,各隐变量之间条件独立。
{
P
(
h
(
1
)
∣
v
)
=
∏
j
=
1
m
P
(
h
j
(
1
)
∣
v
)
P
(
h
j
(
1
)
∣
v
)
=
Sigmoid
(
∑
i
=
1
n
w
i
j
⋅
v
i
(
1
)
+
c
j
)
\begin{cases} \mathcal P(h^{(1)} \mid v) = \prod_{j=1}^m \mathcal P(h_j^{(1)} \mid v) \\ \mathcal P(h_j^{(1)} \mid v) = \text{Sigmoid} \left(\sum_{i=1}^n w_{ij} \cdot v_i^{(1)} + c_j\right) \end{cases}
{P(h(1)∣v)=∏j=1mP(hj(1)∣v)P(hj(1)∣v)=Sigmoid(∑i=1nwij⋅vi(1)+cj)
那么自然可以实现
Q
(
h
(
1
)
∣
v
)
=
P
(
h
(
1
)
∣
v
)
\mathcal Q(h^{(1)} \mid v) = \mathcal P(h^{(1)} \mid v)
Q(h(1)∣v)=P(h(1)∣v)。
那么如果变成了深度信念网络的网络结构,那么关于隐变量的后验概率
P
(
h
(
1
)
∣
v
)
\mathcal P(h^{(1)} \mid v)
P(h(1)∣v)是否还可以直接进行求解?自然是不行的。
相比于受限玻尔兹曼机,深度信念网络中的
P
(
h
(
1
)
∣
v
)
\mathcal P(h^{(1)} \mid v)
P(h(1)∣v)是有向图结构,并且是
V
\mathcal V
V型结构,此时
h
(
1
)
h^{(1)}
h(1)中的隐变量结点之间并不是条件独立关系。如果通过积分的方式进行求解:
P
(
h
(
1
)
∣
v
)
=
∑
h
(
2
)
,
h
(
3
)
P
(
h
∣
v
)
\mathcal P(h^{(1)} \mid v) = \sum_{h^{(2)},h^{(3)}} \mathcal P(h \mid v)
P(h(1)∣v)=h(2),h(3)∑P(h∣v)
h
(
2
)
,
h
(
3
)
h^{(2)},h^{(3)}
h(2),h(3)层之间无向图结构的计算过程中也是非常复杂。因此,在深度信念网络中,
Q
(
h
(
1
)
∣
v
)
\mathcal Q(h^{(1)} \mid v)
Q(h(1)∣v)就是关于后验分布
P
(
h
(
1
)
∣
v
)
\mathcal P(h^{(1)} \mid v)
P(h(1)∣v)的一个近似分布。
那么 Q ( h ( 1 ) ∣ v ) \mathcal Q(h^{(1)} \mid v) Q(h(1)∣v)如何求解?观察深度信念网络的学习过程:
- 从观测变量层
v
(
1
)
v^{(1)}
v(1)到隐变量层
h
(
1
)
h^{(1)}
h(1)开始,他的结构如下:
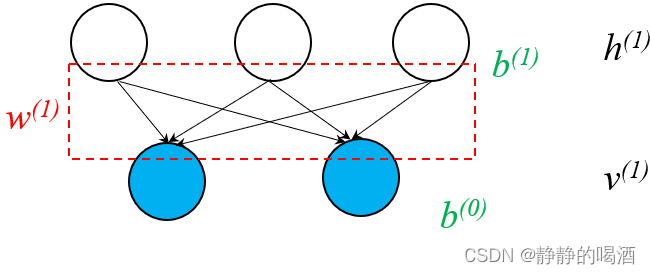
但从这个结构观察,它就是一个贝叶斯网络。由于 V \mathcal V V型结构,没有办法对 P ( h ( 1 ) ∣ v ( 1 ) ) \mathcal P(h^{(1)} \mid v^{(1)}) P(h(1)∣v(1))直接求解。那么贪心逐层预训练的思想是:将上述结构视作受限玻尔兹曼机,对玻尔兹曼机的后验进行求解:如果视作’受限玻尔兹曼机‘,h ( 1 ) h^{(1)} h(1)的隐变量结点之间自然是条件独立,并且能够直接求解。这个后验结果自然不是P ( h ( 1 ) ∣ v ( 1 ) ) \mathcal P(h^{(1)} \mid v^{(1)}) P(h(1)∣v(1)),但将该结果视作它的近似分布Q ( h ( 1 ) ∣ v ( 1 ) ) \mathcal Q(h^{(1)} \mid v^{(1)}) Q(h(1)∣v(1)).这里的贪心思想自然是指:无论后续堆叠了多少层(受限玻尔兹曼机)结构,这里仅观察当前层的权重信息。其中W i ( 1 ) \mathcal W_i^{(1)} Wi(1)表示隐变量结点h i ( 1 ) h_i^{(1)} hi(1)与v ( 1 ) v^{(1)} v(1)各结点连接的边的权重信息。即:W i ( 1 ) = ( W h i ( 1 ) ⇔ v 1 ( 1 ) , W h i ( 1 ) ⇔ v 2 ( 1 ) , ⋯ , W h i ( 1 ) ⇔ v ∣ D ∣ ( 1 ) ) ∣ D ∣ × 1 T \mathcal W_i^{(1)} = \left(\mathcal W_{h_i^{(1)} \Leftrightarrow v_1^{(1)}},\mathcal W_{h_i^{(1)} \Leftrightarrow v_2^{(1)}},\cdots,\mathcal W_{h_i^{(1)} \Leftrightarrow v_{|\mathcal D|}^{(1)}}\right)_{|\mathcal D| \times 1}^T Wi(1)=(Whi(1)⇔v1(1),Whi(1)⇔v2(1),⋯,Whi(1)⇔v∣D∣(1))∣D∣×1T
Q ( h ( 1 ) ∣ v ) = ∏ h i ( 1 ) ∈ h ( 1 ) Q ( h i ( 1 ) ∣ v ( 1 ) ) = ∏ h i ( 1 ) ∈ h ( 1 ) Sigmoid ( W i ( 1 ) ⋅ v ( 1 ) + b i ( 1 ) ) \begin{aligned} \mathcal Q(h^{(1)} \mid v) & = \prod_{h_{i}^{(1)} \in h^{(1)}} \mathcal Q(h_i^{(1)} \mid v^{(1)}) \\ & = \prod_{h_i^{(1)} \in h^{(1)}} \text{Sigmoid} \left(\mathcal W_i^{(1)} \cdot v^{(1)} + b_i^{(1)}\right) \end{aligned} Q(h(1)∣v)=hi(1)∈h(1)∏Q(hi(1)∣v(1))=hi(1)∈h(1)∏Sigmoid(Wi(1)⋅v(1)+bi(1))
- 此时,关于
h
(
1
)
h^{(1)}
h(1)的后验分布
Q
(
h
(
1
)
∣
v
)
\mathcal Q(h^{(1)} \mid v)
Q(h(1)∣v)求解之后,可以基于该分布获取样本。此时不再关注
v
(
1
)
v^{(1)}
v(1)层,
h
(
1
)
h^{(1)}
h(1)层由于样本的产生成为了新的观测变量层:
将初始的观测变量通过Sigmoid \text{Sigmoid} Sigmoid运算得到相同数量的关于h ( 1 ) h^{(1)} h(1)的后验样本。
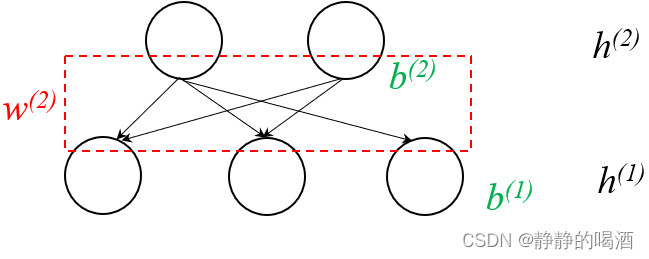
继续执行上述操作:
这里就直接公式表示,不再过多描述。
Q ( h ( 2 ) ∣ h ( 1 ) ) = ∏ h j ( 2 ) ∈ h ( 2 ) Q ( h j ( 2 ) ∣ h ( 1 ) ) = ∏ h j ( 2 ) ∈ h ( 2 ) Sigmoid ( W j ( 2 ) ⋅ h ( 1 ) + b j ( 2 ) ) \begin{aligned} \mathcal Q(h^{(2)} \mid h^{(1)}) & = \prod_{h_j^{(2)} \in h^{(2)}} \mathcal Q(h_j^{(2)} \mid h^{(1)}) \\ & = \prod_{h_j^{(2)} \in h^{(2)}}\text{Sigmoid} \left(\mathcal W_j^{(2)} \cdot h^{(1)} + b_j^{(2)}\right) \end{aligned} Q(h(2)∣h(1))=hj(2)∈h(2)∏Q(hj(2)∣h(1))=hj(2)∈h(2)∏Sigmoid(Wj(2)⋅h(1)+bj(2)) - 以此类推,直到最后一层。至此,可以将模型结构中所有结点的后验信息进行求解。
后续的层可能是真正的’受限玻尔兹曼机‘,就没有必要去’视作‘了~
实际上,贪心逐层预训练算法中核心思想是:从观测变量层开始遍历,如果是
Sigmoid
\text{Sigmoid}
Sigmoid信念网络的结构(有向图结构),将其视作对应的无向图结构(受限玻尔兹曼机),求出的后验分布
Q
(
h
∣
v
)
\mathcal Q(h \mid v)
Q(h∣v)来替代真正的后验分布
P
(
h
∣
v
)
\mathcal P(h \mid v)
P(h∣v)。
由于
Q
(
h
∣
v
)
\mathcal Q(h \mid v)
Q(h∣v)和
P
(
h
∣
v
)
\mathcal P(h \mid v)
P(h∣v)之间的误差是迭代一开始出现的,后续即便存在无向图结构,这个误差也是只大不小。
这就意味着,贪心逐层预训练算法得到的模型参数对应的 ELBO \text{ELBO} ELBO结果可能并不优秀。这也是深度信息网络结构的缺陷之一。相比之下,深度玻尔兹曼机 不会出现上述误差情况。
但深度信念网络同样有它的优点:样本的生成过程更加方便。
- 受限玻尔兹曼机部分样本的生成过程是复杂的。因为使用吉布斯采样时需要达到平稳分布。即便是通过对比散度的方式加快采样效率,但依然是十分复杂的;
- 而 Sigmoid \text{Sigmoid} Sigmoid信念网络部分的采样是基于祖先采样方法进行采样,采样效率极高。
至此,关于深度信念网络部分暂时介绍到这里。下一节将介绍深度玻尔兹曼机(Deep Boltzmann Machine,DBM),并观察两种模型之间的区别以及优缺点。
相关参考:
(系列二十七)深度信念网络4-贪心逐层预训练