力扣算法(Java实现)—数组入门（11题）

news2024/11/23 23:33:41

文章目录

        • 1.删除排序数组中的重复项
        • 2.买卖股票的最佳时机 II
        • 3.旋转数组
        • 4.存在重复元素
        • 5.找出只出现一次的元素
        • 6.两个数组的交集
        • 7.移动零
        • 8.加一
        • 9.两数之和
        • 10.有效的数独
        • 11.旋转图像

💎💎💎💎💎

更多资源链接，欢迎访问作者gitee仓库：https://gitee.com/fanggaolei/learning-notes-warehouse/tree/master

哔哩哔哩算法题视频讲解：Java初级算法合集

1.删除排序数组中的重复项

给你一个 升序排列 的数组 nums ，请你 原地删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。

不要使用额外的空间，你必须在 原地修改输入数组 并在使用 O(1) 额外空间的条件下完成。

输入：nums = [0,0,1,1,1,2,2,3,3,4]
输出：5, nums = [0,1,2,3,4]
解释：函数应该返回新的长度 5 ， 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。

class Solution {
    public int removeDuplicates(int[] nums) {
        if (nums== null || nums.length == 0) { //边界条件
            return 0;
        }
        
        int i=0;
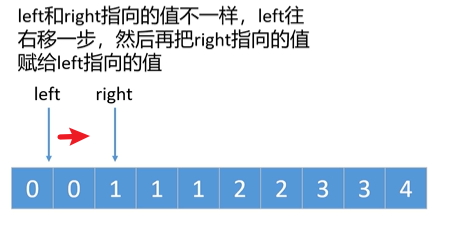
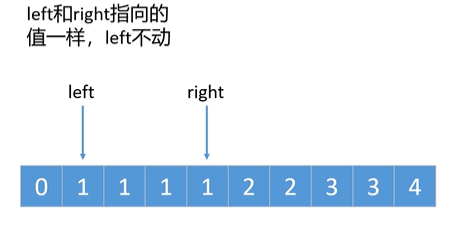
        for(int j = 1; j < nums.length; j++){    //右指针始终向右移动，而左指针在特定条件下才会移动
            //如果左指针和右指针指向的值一样，说明有重复的，
            //这个时候，左指针不动，右指针继续往右移。如果他俩
            //指向的值不一样就把右指针指向的值往前挪
            if(nums[i] != nums[j]){
                i = i + 1;
                nums[i] = nums[j];
            }
        }
        return i+1;
    }
}

image-20221207120704883

涉及知识点：使用双指针解决问题

使用两个指针，右指针始终往右移动

  • 如果右指针指向的值等于左指针指向的值，左指针不动。
    如果右指针指向的值不等于左指针指向的值，那么左指针往右移一步，然后再把右指针指向的值赋给左指针。

image-20220916090051872

image-20220916090114963

第二种解题方式：

class Solution {
     public int removeDuplicates(int[] A) {
        int count = 0;//重复的数字个数
        for (int right = 1; right < A.length; right++) {
            if (A[right] == A[right - 1]) {
                //如果有重复的，count要加1
                count++;
            } else {
                //如果没有重复，后面的就往前挪
                A[right - count] = A[right];
            }
        }
        //数组的长度减去重复的个数
        return A.length - count;
    }
}

这里的count用于计数，先确定有多少个值是重复的，再将后面不重复的值赋值给前面应该修改的值

image-20221207120632034

2.买卖股票的最佳时机 II

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在 同一天 出售。

返回 你能获得的 最大 利润 。

输入：prices = [1,2,3,4,5]
输出：4
解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。
     总利润为 4 。

public class test2 {
    public static void main(String[] args) {
        int[] arr1=new int[]{1,2,6,9,1,5};
        System.out.println(maxProfit(arr1));
    }

    public static int maxProfit(int[] prices) {
        int max = 0;
        for (int i = 1; i < prices.length; i++) {
            if (prices[i] > prices[i - 1]) {
                max = max + (prices[i] - prices[i - 1]);
            }
        }
        return max;
    }
}

image-20221207120515423

3.旋转数组

给你一个数组，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。

示例 1:

输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]

public class test {
    public static void main(String[] args) {

        int k=3;
        int[]arr=new int[]{1,2,3,4,5,6,7};//5 6 7 1 2 3 4
        Solution solution = new Solution();
        solution.twoSum(arr,k);
    }
}

class Solution {
    public void rotate(int[] nums, int k) {
        int length=nums.length;
        k=k%nums.length;
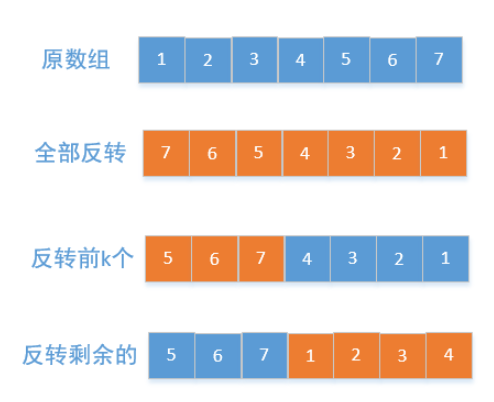
        reverse(nums, 0, length - 1);//旋转全部7 6 5 4 3 2 1 
        reverse(nums,0,k-1); //旋转前部分 5 6 7 4 3 2 1
        reverse(nums,k,length-1); //旋转后部分 5 6 7 1 2 3 4

    }

    public void reverse(int [] nums, int start ,int end){
		/**
         * 6->0
         * 5->1
         * 4->2
         */
        while (start<end){
            int tmp=nums[start];
            nums[start]=nums[end];
            nums[end]=tmp;
            start++;
            end--;
        }
    }
}

class Solution {
    public void rotate(int[] nums, int k) {
        
        int[] tmp=new int[nums.length];

        int j=0;
        for(int i=0;i<nums.length;i++){
            tmp[j++]=nums[i];
        }

        for(int e=0;e<nums.length;e++){
            nums[(e+k)%nums.length]=tmp[e];
        }

    }
}

image-20221231171745458

image-20221207120454868

4.存在重复元素

示例 1：

输入：nums = [1,2,3,1]
输出：true

示例 2：

输入：nums = [1,2,3,4]
输出：false

示例 3：

输入：nums = [1,1,1,3,3,4,3,2,4,2]
输出：true

import java.util.Arrays;

public class test {
    public static void main(String[] args) {
        Solution solution=new Solution();
        int[]arr=new int[]{2,1,5,2,4,5,6};
        solution.containsDuplicate(arr);
    }
}

//先排序后比较
class Solution {
    public boolean containsDuplicate(int[] nums) {
        Arrays.sort(nums); //对数组进行排序
        for (int ind = 1; ind < nums.length; ind++) {
            if (nums[ind] == nums[ind - 1]) {
                return true;
            }
        }
        return false;
    }
}

image-20221207120429116

   public boolean containsDuplicate(int[] nums) {
        Set<Integer> set = new HashSet<>();
        for (int num : nums) {
            //因为集合set中不能有重复的元素，如果有重复的
            //元素添加，就会添加失败
            if (!set.add(num))
                return true;
        }
        return false;
    }

image-20230101190325013

5.找出只出现一次的元素

给你一个 非空 整数数组 nums ，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

你必须设计并实现线性时间复杂度的算法来解决此问题，且该算法只使用常量额外空间。

示例 1 ：

输入：nums = [2,2,1]
输出：1

示例 2 ：

输入：nums = [4,1,2,1,2]
输出：4

示例 3 ：

输入：nums = [1]
输出：1

public class test {
    public static void main(String[] args) {
        Solution solution=new Solution();
        int[]arr=new int[]{1,2,1,2,3};
        solution.singleNumber(arr);
    }
}

class Solution {
    public int singleNumber(int[] nums) {
        Set<Integer> set = new HashSet<>();
        for (int num : nums) {
            if (!set.add(num)) {
                //如果添加失败，说明这个值
                //在集合Set中存在，我们要
                //把他给移除掉
                set.remove(num);
            }
        }
        //最终集合Set中只有一个元素，我们直接返回
        return (int) set.toArray()[0];
    }
}

image-20221207120407628

class Solution {
    public int singleNumber(int[] nums) {

        Arrays.sort(nums);

        if(nums.length==1){
            return nums[0];
        }
        
        for(int i=0;i<nums.length-1;i++){
            if(nums[i]==nums[i+1]){
                i++;
            }else{
                return nums[i];
            }
        }  
    return nums[nums.length-1];
    }
}

image-20230102142455948

public class test {
    public static void main(String[] args) {

        /**
         * 2 0010
         * 2 0010 0000
         * 3 0011 0011
         * 3 0011 0000
         * 4 0100 0100
         */

        System.out.println(2^2^3^3^4);

    }
}


class Solution {
    public int singleNumber(int[] nums) {
        int reduce=0;
        for(int num:nums){
            reduce=reduce^num;
        }
        return reduce;
    }
}

image-20230102164323089

6.两个数组的交集

示例 1：

输入：nums1 = [1,2,2,1], nums2 = [2,2]
输出：[2,2]

示例 2:

输入：nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出：[4,9]

class Solution {
    public int[] intersect(int[] nums1, int[] nums2) {
        int len1 = nums1.length, len2 = nums2.length;
        int len = len1<len2?len1:len2;
        int[] ans = new int[len];
        if(len1 == 0 || len2 == 0){  //处理边界条件
            return ans;
        }
        Arrays.sort(nums1);
        Arrays.sort(nums2);
        int i=0, j=0, k=0;
        while(i<len1 && j<len2){
            if(nums1[i] == nums2[j]){
                ans[k++] = nums1[i];
                i++;
                j++;
            }else if(nums1[i] < nums2[j]){
                i++;
            }else{
                j++;
            }
        }
        return Arrays.copyOfRange(ans, 0, k);
    }
}

image-20230102180134275

7.移动零

示例 1:

输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]

示例 2:

输入: nums = [0]
输出: [0]

class Solution {
        public void moveZeroes(int[] nums) {
        int i = 0;//统计前面0的个数
        for (int j = 0; j < nums.length; j++) {
            if (nums[j] == 0) {//如果当前数字是0就不操作
                i++;
            } else if (i != 0) {
                //否则，把当前数字放到最前面那个0的位置，然后再把
                //当前位置设为0
                nums[j - i] = nums[j];
                nums[j] = 0;
            }
        }
    }
}

image-20230103160453807

8.加一

示例 1：

输入：digits = [1,2,3]
输出：[1,2,4]

解释：输入数组表示数字 123。
示例 2：

输入：digits = [4,3,2,1]
输出：[4,3,2,2]

解释：输入数组表示数字 4321。
示例 3：

输入：digits = [0]
输出：[1]

  public int[] plusOne(int[] digits) {
        int length = digits.length;
        for (int i = length - 1; i >= 0; i--) {
            if (digits[i] != 9) {
                //如果数组当前元素不等于9，直接加1
                //然后直接返回
                digits[i]++;
                return digits;
            } else {
                //如果数组当前元素等于9，那么加1之后
                //肯定会变为0，我们先让他变为0
                digits[i] = 0;
            }
        }
        //除非数组中的元素都是9，否则不会走到这一步，
        //如果数组的元素都是9，我们只需要把数组的长度
        //增加1，并且把数组的第一个元素置为1即可
        int temp[] = new int[length + 1];
        temp[0] = 1;
        return temp;
    }

image-20230103160516580

9.两数之和

示例 1：

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

示例 2：

输入：nums = [3,2,4], target = 6
输出：[1,2]

示例 3：

输入：nums = [3,3], target = 6
输出：[0,1]

class Solution {
    public int[] twoSum(int[] nums, int target) {
        
        for(int i=0;i<nums.length;i++){
            for(int j=i+1;j<nums.length;j++){
                if(nums[i]+nums[j]==target){
                    return new int[]{i,j};
                }
            
            }
        }
        return new int[]{-1,-1};

    }
}

image-20230108163856173

10.有效的数独

请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ，验证已经填入的数字是否有效即可。

数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）

注意：

一个有效的数独（部分已被填充）不一定是可解的。只需要根据以上规则，验证已经填入的数字是否有效即可。
空白格用 ‘.’ 表示。

示例 1：

输入：board = 
[["5","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出：true

示例 2：

输入：board = 
[["8","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]

输出：false
解释：除了第一行的第一个数字从 5 改为 8 以外，空格内其他数字均与 示例1 相同。 但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。

class Solution {
    public boolean isValidSudoku(char[][] board) {
        for(int i=0;i<9;i++){
            HashSet set1=new HashSet();
            HashSet set2=new HashSet();
            HashSet set3=new HashSet();
            for(int j=0;j<9;j++){
                if(board[i][j]!='.'&&!set1.add(board[i][j])){
                    return false;
                }
                if(board[j][i]!='.'&&!set2.add(board[j][i])){
                    return false;
                }
                int a=(i/3)*3+j/3;
                int b=(i%3)*3+j%3;
                if(board[a][b]!='.'&&!set3.add(board[a][b])){
                    return false;
                }

            }
        }
    return true;
    }
}

image-20230108163921765

这样做其实就是做成了9个九宫格 拿第一个做起点 那么9个元素分别为(0,0) (0,1)(0,2) 这几个位置分别对应得J得值是1-9
(1,0) (1,1)(1,2)
(2,0) (2,1)(2,2)
假设行为a 列为b从这个9宫格位置可以看出 a=j/3 b=j%3 (从第一个元素看 位置索引为0,0对应J=1) 这里要注意下int类型去余（既（int）1.8=1 (int)0.8=0） 这样得出行列与j得关系：a=j/3 b=j%3
同理总共9个九宫格 我们则需要找到9个起点即可 这里看去起点为(0,0) (0,3) (0,6)
(3,0) (3,3) (3,6)
(6,0) (6,3) (6,6)
这样得出起点关系为 qA = (i/3)*3 qB =（i%3）*3
这样每个起点都能带入开始推导得公式 则得出箱子元素得对应关系为 a=j/3+(i/3)*3
b=j%3+(i%3)*3

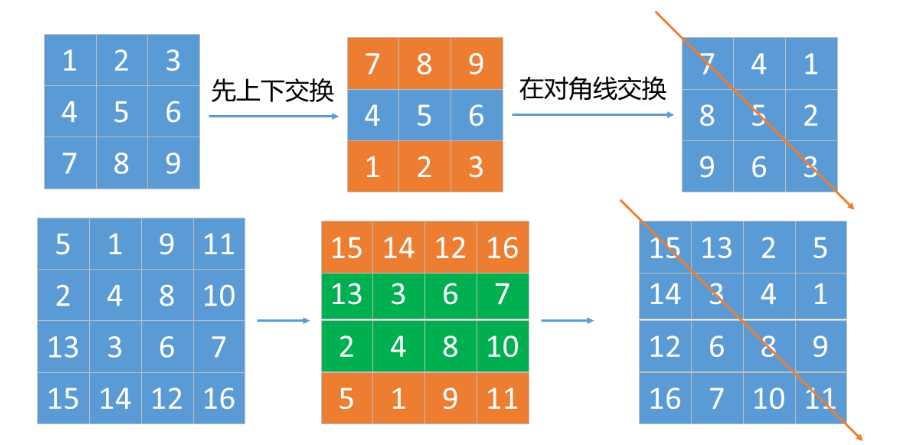
11.旋转图像

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

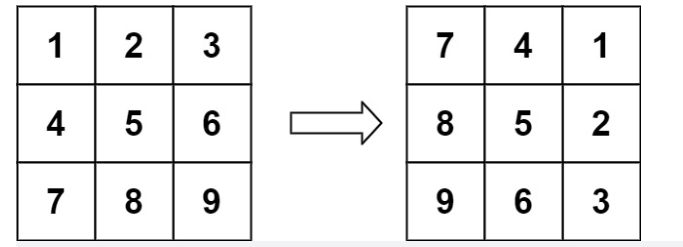
image-20230112205126734

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

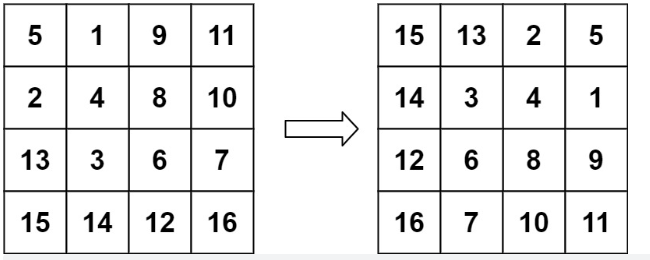
image-20230112205137669

输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

class Solution {
    public void rotate(int[][] matrix) {

        int length=matrix.length;
        for(int i=0;i<matrix.length/2;i++){
            int[] tmp=matrix[i];
            matrix[i]=matrix[length-1];
            matrix[length-1]=tmp;
            length--;
        }
        for(int i=0;i<matrix.length;i++){
            for(int j=i+1;j<matrix.length;j++){
                int tmp=matrix[i][j];
                matrix[i][j]=matrix[j][i];
                matrix[j][i]=tmp;
            }
        }

    }
}

image-20230112205205254

image-20230112205151185

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/158279.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【手写 Vue2.x 源码】第十八篇 - 根据 render 函数，生成 vnode

【手写 Vue2.x 源码】第十八篇 - 根据 render 函数，生成 vnode

一&#xff0c;前言 上篇&#xff0c;介绍了render 函数的生成&#xff0c;主要涉及以下两点&#xff1a; 使用 with 对生成的 code 进行一次包装将包装后的完整 code 字符串&#xff0c;通过 new Function 输出为 render 函数 本篇&#xff0c;根据 render 函数&#xff0c…
阅读更多...
linux系统中QT里面的视频播放器的实现方法

linux系统中QT里面的视频播放器的实现方法

大家好&#xff0c;今天主要和大家聊一聊&#xff0c;如何使用QT中视频播放器的方法。 目录 第一&#xff1a;视频播放器基本简介 第二&#xff1a;视频播放器头文件说明 第三&#xff1a;源文件的具体实现方法 第四&#xff1a;运行效果显示 第一&#xff1a;视频播放器基本…
阅读更多...
ADS振铃仿真

ADS振铃仿真

目录 无振铃时的原理图 无振铃时的Vout和VL输出波形 ​LineCalc对微带线阻抗的计算结果 将微带线线宽Width统一由116改为130 将微带线线宽Width统一由116改为80 将微带线TL9线宽由116改为300 将微带线TL9线宽由116改为50 本文介绍了微带线线宽变化时100MHz信号的反射现象…
阅读更多...
2023 年 15 大测试自动化趋势

2023 年 15 大测试自动化趋势

在过去&#xff0c;软件测试只是为了发现软件产品中的错误。目标是——提高软件质量。但如今&#xff0c;软件测试的范围已经扩大。在软件测试方面&#xff0c;自动化测试一直走在前列。按照最新的测试自动化趋势&#xff0c;软件测试行业有望比过去十年发展得更快。 根据 Mar…
阅读更多...
Java面向对象综合训练

Java面向对象综合训练

Java面向对象综合训练一、文字版格斗游戏Role类测试类输出结果二、对象数组练习对象数组1商品类测试类输出结果对象数组2汽车类测试类输出结果对象数组3手机类测试类输出结果对象数组4女朋友类测试类输出结果对象数组5学生类测试类输出结果一、文字版格斗游戏 Role类 import j…
阅读更多...
去掉 域名后面的 /#/ vue-router 和 hbuilder发布 web项目和h5项目

去掉 域名后面的 /#/ vue-router 和 hbuilder发布 web项目和h5项目

1. vue-router vue-router默认的路由模式是hash&#xff0c;我们要去掉url中的#需要将路由模式切换为history const router new VueRouter({base: test, // 如果项目项目在 域名 根目录下&#xff0c;则去掉这行mode: history, // 路由模式... })这样子&#xff0c;url中的#…
阅读更多...
为什么ERP和项目管理的集成是必要的？

为什么ERP和项目管理的集成是必要的？

在一个企业中&#xff0c;传统的责任分工意味着会计人员看管资金和维持财务标准&#xff0c;而职能经理分配人力资源和维持技术标准。项目经理指导分配的资金和其他资源&#xff0c;同时努力实现项目目标。每个学科都有自己的业务规则&#xff0c;自己的做法&#xff0c;自己的…
阅读更多...
C++ | 左值、右值、将亡值和引用的概念 | 聊聊我对它们的深入理解

C++ | 左值、右值、将亡值和引用的概念 | 聊聊我对它们的深入理解

文章目录前言左右值的辨析一个特殊的问题将亡值引用的深刻理解前言 这篇文章是我在探究完美转发这个语法点时&#xff0c;引发的相关问题思考&#xff0c;为了使自己的理解更深刻&#xff0c;故写下这篇博客 左右值的辨析 首先需要明白两个概念&#xff1a;类型&#xff08;…
阅读更多...
1577_AURIX_TC275_MTU中检测控制相关寄存器

1577_AURIX_TC275_MTU中检测控制相关寄存器

全部学习汇总&#xff1a; GreyZhang/g_TC275: happy hacking for TC275! (github.com) 开篇介绍的功能室之前看过很多次的一个握手的功能。快速行以及快速列模式的测试中&#xff0c;这个行列其实是对应的存储的bit阵列信息。一个对应相应的字&#xff0c;另一个则对应bit序列…
阅读更多...
【Linux】进程创建、终止、等待、替换、shell派生子进程的理解…

【Linux】进程创建、终止、等待、替换、shell派生子进程的理解…

柴犬&#xff1a; 你好啊&#xff0c;屏幕前的大帅哥or大美女&#xff0c;和我一起享受美好的今天叭&#x1f603;&#x1f603;&#x1f603; 文章目录一、进程创建1.调用fork之后&#xff0c;内核都做了什么&#xff1f;2.如何理解fork函数有两个返回值&#xff1f;3.如何理…
阅读更多...
（短信服务）java SpringBoot 阿里云短信功能实现发送手机验证码

（短信服务）java SpringBoot 阿里云短信功能实现发送手机验证码

一.阿里云准备工作 1.阿里云短信服务-注册账号 阿里云官网: https://www.aliyun.com/ 点击官网首页注册按钮。 2.阿里云短信服务-设置短信签名&#xff08;阿里云提供测试的签名&#xff0c;暂时可以跳过&#xff09; 注册成功后&#xff0c;点击登录按钮进行登录。登录后…
阅读更多...
简单方式调用WebService服务

简单方式调用WebService服务

好久没有进行过WebService开发了&#xff0c;由于项目需要&#xff0c;重拾WebService&#xff0c;记录一下简单的服务调用方法。拿到需求&#xff0c;仅半页word&#xff0c;其他的就没有了&#xff0c;为了快速开发&#xff0c;尝试过使用插件逆向生成调用的一大堆类&#xf…
阅读更多...
AWVS安装与激活

AWVS安装与激活

AWVS安装与激活 1.AWVS简介 AWVS&#xff08;Acunetix Web Vulnerability Scanner&#xff09;是一款知名的网络漏洞扫描工具&#xff0c;通过网络爬虫测试网站安全&#xff0c;检测流行的Web应用攻击&#xff0c;如跨站脚本、sql 注入等。据统计&#xff0c;75% 的互联网攻击…
阅读更多...
pmp备考全攻略

pmp备考全攻略

我这里分享一下我备考的经验&#xff0c;如何对大家有帮助也可以稍微给点支持&#xff0c;让更多人了解&#xff01; 一&#xff0c;我的pmp备考经验 1.一阶段&#xff1a;铺底&#xff0c;花费时间1.5周左右 主要是熟悉考试框架和内容&#xff0c;通过看网盘资料里的章节重…
阅读更多...
vue3+ts实现自定义按钮导航

vue3+ts实现自定义按钮导航

效果图 点击对应按钮&#xff0c;相应按钮被激活&#xff0c;背景平移至激活按钮&#xff0c;字体高亮&#xff0c;其余按钮重置&#xff0c;由于ele没有类似tab&#xff0c;就简单记录下。 实现 <template><div class"tab_wrapper"><spanv-for&q…
阅读更多...
这些技巧你值得学会

这些技巧你值得学会

技巧一&#xff1a;多图合并为PDF文件 处理合并多份PDF文件外&#xff0c;使用PS的【PDF演示文稿】工具&#xff0c;也能一同将多张图片合并成PDF文档&#xff01;通过合并的方式&#xff0c;不但能够批量归纳汇总图片&#xff0c;而且还能根据自身需求&#xff0c;将图片与PD…
阅读更多...
Visual studio C++程序内使用Sqlite3

Visual studio C++程序内使用Sqlite3

Visual studio C程序内使用Sqlite3 前言 本篇讲解了如何在Visual studio开发的C桌面应用程序内使用Sqlite数据库&#xff0c;Sqlite的语法和Mysql是一样的&#xff0c;所以本篇文章不对数据库语法做过多介绍&#xff0c;介绍一些常用Sqlite的API ★提高阅读体验★ &…
阅读更多...
二叉树常见题目

二叉树常见题目

目录 一、判断一棵树是否为另一棵树的子树 二、判断是否对称二叉树 三、翻转二叉树 四、二叉树构建及遍历 五、根据二叉树创建字符串 六、二叉树的最近公共祖先 七、根据前序遍历和中序遍历构造二叉树 八、根据后序遍历和中序遍历构造二叉树 九、二叉树前序非递归…
阅读更多...
MySQL——“order by”是如何工作的

MySQL——“order by”是如何工作的

假设目前有这么一个表 CREATE TABLE t (id int(11) NOT NULL,city varchar(16) NOT NULL,name varchar(16) NOT NULL,age int(11) NOT NULL,addr varchar(128) DEFAULT NULL,PRIMARY KEY (id),KEY city (city) ) ENGINEInnoDB; 业务要求是要查询城市是“杭州”的所有人名字&a…
阅读更多...
1.2计算机系统的层次结构

1.2计算机系统的层次结构

文章目录&#xff08;1&#xff09;微指令&#xff08;2&#xff09;汇编语言&#xff08;3&#xff09;高级语言&#xff08;4&#xff09;操作系统&#xff08;5&#xff09;编译程序与解释程序&#xff08;6&#xff09;总结请先食用这一篇 计算机工作过程&#xff08;1&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023