一、实验目的

1. 了解一些常用随机噪声的生成方法。
2. 掌握根据指定退化函数对图像进行退化的方法。
3. 掌握当模糊图像只存在噪声时的几种滤波复原方法。
4. 掌握当模糊图像同时存在线性退化和噪声时的几种滤波复原方法。

二、实验例题

1. 噪声模型

由函数 imnoise2(在文件夹“实验 4_实验材料_图像+程序”中已给出)可生成指定类型的大小为$M\times N$的随机噪声数组$R$，与 imnoise 函数输出一幅有噪声的图像不同的是，函数 imnoise2 生成噪声模式本身，其可生成的噪声类型如表 1 所示。

2. 只存在噪声的滤波——空间滤波

当一幅图像中唯一存在的退化是噪声时， 式$(1)$和式$(2)$变成式$(4)$和式$(5)$：

$$g(x)=f(x)+\eta (x,y)\text{\hspace{1em}(4)}$$
$$G(u,v)=F(u,v)+N(u,v)\text{\hspace{1em}(5)}$$
表 2 列出了一些常用的空间滤波器，其中，$S_{xy}$表示输入噪声图像 $g$ 的 $m\times n$子图像区域。 S 的下标表示子图像中心的坐标$(x,y)$，$\hat{f}(x,y)$( f 的一个估值)表示滤波器在这些坐标处的响应。

例 2 图 3 给出了两幅含噪声的电路图像，其中图 3(a)所示的是一幅被概率密度为 0.1的胡椒噪声污染的图像， 图 3(b)所示的是一幅被相同概率密度的盐粒噪声污染的图像。
请进行以下操作：
(1) 使用大小为$3\times 3$、阶数为 1.5 的逆谐波均值滤波器分别对图 3(a)和图 3(b)进行滤波处理。
(2) 使用大小为$3\times 3$、阶数为-1.5 的逆谐波均值滤波器分别对图 3(a)和图 3(b)进行滤波处理。

逆谐波均值滤波器 Contra-Harmonic Mean Filter其公式如下：
$$f(x,y)=\frac{{\sum }_{(x,y)\in S_{xy}}g(s,t{)}^{Q+1}}{{\sum }_{(x,y)\in S_{xy}}g(s,t{)}^Q}$$

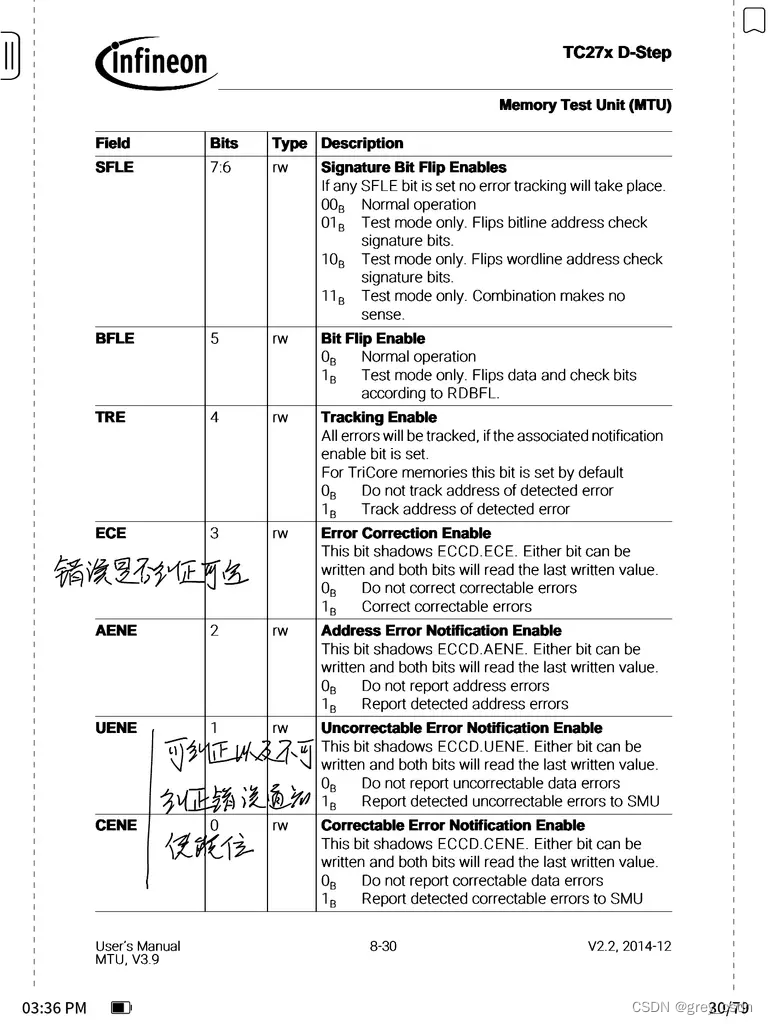
其中Q称为滤波器的阶数，该滤波器可以用来消除椒盐噪声。但是需要不同同时处理盐粒噪声和胡椒噪声，当Q为正时，可以消除胡椒噪声；当Q为负时，消除盐粒噪声。当Q=0时，该滤波器退化为算术均值滤波器；Q=-1时，退化为谐波均值滤波器。

关于逆谐波滤波器的思考
$$\hat{f}(x,y)=\sum \frac{g(s,t{)}^{Q}g(s,t)}{\sum g(s,t{)}^Q}=\sum \frac{g(s,t{)}^Q}{\sum g(s,t{)}^Q}g(s,t)=\sum \frac{g(s,t{)}^Q}{A}g(s,t)$$
上式可看做求$(x,y)$邻域内所有$(s,t)$点的加权平均值，权重的分母${\sum }_{(s,t)\in S_{xy}}g(s,t{)}^Q$是个常数，只需考虑分子$g(s,t{)}^Q$的大小。当$Q>0$时，$g(s,t)$越大，$g(s,t{)}^Q$值越大，对于$g(s,t)$处的加权值结果也就越大，平滑处理后的结果接近较大值。此时，焦噪声被弱化，起到了滤除焦噪声的作用。

反之，$Q<0$的时候，$g(s,t)$越大，$g(s,t{)}^Q$越小，对于$g(s,t)$处的加权值结果也就越小，平稳处理后的结果越接近较小值。此时，盐噪声被弱化，起到了滤除了盐噪声的作用。

灰度图范围一般从0到255，白色为255，黑色为0，故黑白图片也称灰度图像。

(a) 被胡椒噪声污染的图像

(b) 被盐粒噪声污染的图像

图3 含噪声的电路图像

答：
(1)

close all; clear all; clc;
f = imread('例2.被概率密度为0.1的胡椒噪声污染的图像.tif');
m = 3; n = 3;
Q = 1.5;
f = im2double(f);
[M, N] = size(f);
%边界扩展
gp = zeros(M+2, N+2);
gp(2:M+1,2:N+1) = f;
gp(1,:) = gp(2,:); %用图像最外层的值扩展
gp(M+2,:) = gp(M+1,:);
gp(:,1) = gp(:,2);
gp(:,N+2) = gp(:,N+1);
%逆谐波均值滤波
g = zeros(M, N);
for x = 2:M+1
    for y = 2:N+1
    g_m = 0; g_d = 0;
        for i = -1:1
            for j = -1:1
                g_m = g_m + gp(x+i,y+j)^(Q+1);
                g_d = g_d + gp(x+i,y+j)^Q;
            end
        end
        g(x-1,y-1) = g_m/g_d;
    end
end
figure; imshow(g);

Q=1.5 滤波结果

可以看到胡椒噪声被很大程度抑制了。图片整体变得更加白了。

(2)

close all; clear all; clc;
f = imread('例 2.被概率密度为 0.1 的盐粒噪声污染的图像.tif');
m=3; n=3;
Q = 1.5;
f=im2double(f);
[M, N] = size(f);
%边界扩展
gp = zeros(M+2, N+2);
gp(2:M+1,2:N+1) = f;
gp(1,:) = gp(2,:); %用图像最外层的值扩展
gp(M+2,:) = gp(M+1,:);
gp(:,1) = gp(:,2);
gp(:,N+2) = gp(:,N+1);
%逆谐波均值滤波
g = zeros(M, N);
for x = 2:M+1
for y = 2:N+1
g_m = 0; g_d = 0;
for i = -1:1
for j = -1:1

分析：逆谐波均值滤波器适于处理脉冲噪声。当 Q 值为正时，该滤波器消除胡椒噪 声；当Q 值为负时，该滤波器消除盐粒噪声。但是，该滤波器不能同时消除这两种噪声。 在使用该滤波器时，必须知道噪声是暗噪声还是亮噪声，以便为 Q 选择正确的符号。由 本实验我们可以看出，若 Q 的符号选择错误，可能引起灾难性的后果。

3. 退化函数建模

在图像复原问题中，遇到的一个主要退化是图像模糊。由场景和传感器两者产生的模糊可以用空间域或频域的低通滤波器来建模。另一个重要的退化模型是在图像获取时传感器和场景之间的均匀线性运动而产生的图像模糊。我们可以用函数 fspecial 对图像模糊建模：
PSF = fspecial(‘motion’, len, theta);
调用 fspecial 将返回点扩散函数 PSF，它近似于摄像机线性移动 len 个像素的效果。参数theta 以度为单位，以逆时针方向对正水平轴度量。len的默认值是 9， theta 的默认值是 0，在水平方向上它对应于 9 个像素的移动。

使用函数 imfilter 来创建一个已知 PSF 的退化图像：
g = imfilter(f, PSF, ‘circular’);
其中， ‘circular’用来减少边界效应。然后通过添加适当的噪声来构造退化的图像模型：
g = g + noise;
其中， noise 是一幅与 g 大小相同的随机噪声图像。另外，还可根据指定的退化模型对图像进行退化处理。

例 3 图 4 所示的是一幅测试图像，请对其进行运动模糊。

图4 测试图像

答：
方法 1：结合函数 fspecial 和 imfilter

f = imread('例 3.测试图像.tif');
len = 100; theta = -45;
PSF = fspecial('motion', len, theta);
g = imfilter(f, PSF, 'circular');
figure; imshow(g);
imwrite(g,'运动模糊后图像.tif');

放大版原图

(a) 30度偏移

(b) -30度偏移

方法 2： 可根据退化函数$H(u,v)=\frac{T}{\pi (ua+vb)}\sin [\pi (ua+vb)]{\mathrm{e}}^{-\mathrm{j}\pi (ua+vb)}$对图像进行运动模糊

4. 存在线性退化和噪声的滤波

(1) 逆滤波

最简单的图像复原方法是直接做逆滤波，用退化函数除退化图像的傅里叶变换来计算原始图像傅里叶变换的估计$\hat{F}(u,v)$,即
$$\hat{F}(u,v)=\frac{G(u,v)}{H(u,v)}\text{\hspace{1em}(6)}$$

(2) 最小均方误差(维纳)滤波

维纳滤波的目标是找到未污染图像$f$的一个估计$\hat{f}$，使它们之间的均方误差最小。图像的频率域估计如式$(7)$所示：
$$\hat{F}(u,v)=\left[\frac{1}{H(u,v)}\frac{|H(u,v){|}^2}{|H(u,v){|}^2+S_{\eta }(u,v)/S_f(u,v)}\right]G(u,v)\text{\hspace{1em}(7)}$$
其中，$H(u,v)$是退化函数， $S_{\eta }(u,v)=|N(u,v){|}^2$是噪声的功率谱，$S_f(u,v)=|F(u,v){|}^2$是未退化图像的功率谱。注意，若噪声为 0，则噪声功率谱消失，维纳滤波可简化为逆滤波。当我们处理白噪声时，谱$|N(u,v){|}^2$是一个常数， 式$(7)$可简化为：

$$\hat{F}(u,v)=\left[\frac{1}{H(u,v)}\frac{|H(u,v){|}^2}{|H(u,v){|}^2+K}\right]G(u,v)\text{\hspace{1em}(8)}$$
其中， $K$是一个加到$|H(u,v){|}^2$的所有项上的特定常数。

疑惑：$S_f(u,v)$是如何确定的？同时，仅保证谱$|N(u,v){|}^2$是一个常数，未退化图像的功率谱$|F(u,v){|}^2$也会是一个常数吗？

附录