RNN（循环神经网络）是一种在深度学习中常用的神经网络结构，用于处理序列数据。与传统的前馈神经网络不同，RNN通过引入循环连接在网络中保留了历史信息。

RNN中的每个神经元都有一个隐藏状态，它会根据当前输入和前一个时间步的隐藏状态来计算输出和下一个时间步的隐藏状态。

这种循环的结构使得RNN可以在序列数据的处理中考虑到上下文信息。对于每个时间步，RNN都会根据当前输入和前一个时间步的隐藏状态来计算当前时间步的输出和隐藏状态，然后将当前时间步的隐藏状态传递给下一个时间步。

RNN的具体计算可以用如下的公式表示： h_t = f(W_hh * h_{t-1} + W_xh * x_t) y_t = g(W_hy * h_t)

其中，h_t表示当前时间步的隐藏状态，h_{t-1}表示前一个时间步的隐藏状态，x_t表示当前时间步的输入，y_t表示当前时间步的输出。

W_hh、W_xh和W_hy分别表示隐藏状态到隐藏状态、输入到隐藏状态和隐藏状态到输出的权重矩阵。f和g是激活函数。

RNN的优势在于可以处理变长的序列数据，并且能够捕捉到序列数据中的长期依赖关系。它被广泛用于自然语言处理、语音识别、时间序列分析等领域。

然而，标准的RNN在处理长序列时容易出现梯度消失或梯度爆炸的问题，为了解决这些问题，后续的研究提出了一些改进的RNN结构，如长短期记忆网络（LSTM）和门控循环单元（GRU）。这些改进的RNN结构在一定程度上缓解了梯度问题，并取得了更好的性能。

政安晨的个人主页：政安晨

欢迎 👍点赞✍评论⭐收藏

收录专栏: 政安晨的机器学习笔记

希望政安晨的博客能够对您有所裨益，如有不足之处，欢迎在评论区提出指正！

---

理解RNN

目前我们见过的所有神经网络（比如密集连接网络和卷积神经网络）都有一个主要特征，那就是它们都没有记忆。它们对每个输入都是单独处理的，在输入之间没有保存任何状态。这样的神经网络要想处理数据点的序列或时间序列，需要一次性将整个序列输入其中，即将整个序列转换为单个数据点。比如我们在密集连接网络示例中就是这样做的：将5天的数据展平为一个大向量，然后一次性处理。这种网络叫作前馈网络（feedforward network）。

与此相对，当阅读这个句子时，你是在逐字阅读（或者更确切地说，是在逐行扫视），同时会记住前面的内容。这让你可以流畅地理解这个句子的含义。智能生物处理信息是渐进式的，保存一个关于所处理内容的内部模型，这个模型是根据过去的信息构建的，并随着新信息的进入而不断更新。

RNN采用相同的原理（不过是一个极其简化的版本）。它处理序列的方式是：遍历所有序列元素，同时保存一个状态（state），其中包含与已查看内容相关的信息。实际上，RNN是一种具有内部环路（loop）的神经网络，如下图所示（RNN：带有环路的神经网络）：

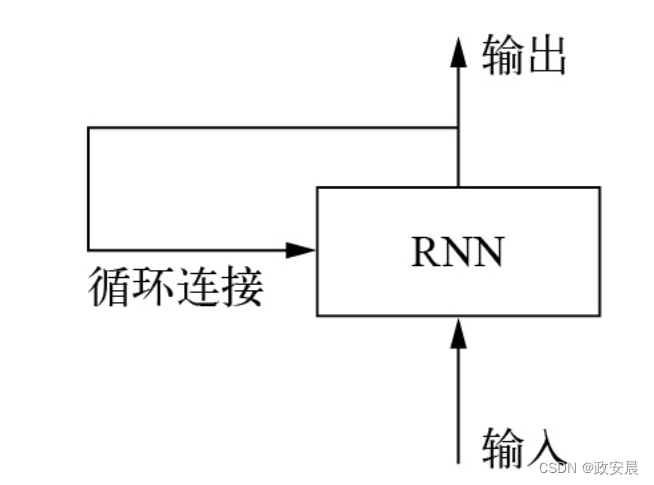
在处理两个彼此独立的序列（比如批量中的两个样本）之间，RNN的状态会被重置，所以你仍然可以将一个序列看作单个数据点，即神经网络的单个输入。不同的是，这个数据点不再是一步处理完，相反，神经网络内部会对序列元素进行循环操作。

为了更好地解释环路和状态的概念，我们来实现一个简单RNN的前向传播。这个RNN的输入是一个向量序列，我们将其编码成尺寸为(timesteps,input_features)的2阶张量。这个RNN对时间步进行遍历，在每个时间步t，它都会考虑t的当前状态和t的输入（形状为(input_features,)），并对二者计算得到t的输出。

然后，我们将下一个时间步的状态设置为上一个时间步的输出。对于第一个时间步，上一个时间步的输出没有定义，所以它没有当前状态。因此，我们将状态初始化为全零向量，这叫作神经网络的初始状态。

RNN伪代码如下所示：

# t的状态
state_t = 0

# 对序列元素进行遍历
for input_t in input_sequence:

    output_t = f(input_t, state_t)

    # 上一次的输出变为下一次迭代的状态
    state_t = output_t

你甚至可以给出具体的f函数：它是从输入和状态到输出的变换，其参数包括两个矩阵（W和U）和一个偏置向量，如下代码所示（更详细的RNN伪代码）。

（它类似于前馈网络中密集连接层所做的变换。）

state_t = 0
for input_t in input_sequence:
    output_t = activation(dot(W, input_t) + dot(U, state_t) + b)
    state_t = output_t

为了将这些概念解释清楚，我们用NumPy来实现简单RNN的前向传播，代码如下所示：

import numpy as np

# 输入序列的时间步数
timesteps = 100 

# 输入特征空间的维度
input_features = 32

# 输出特征空间的维度
output_features = 64

# 输入数据：随机噪声，仅作为示例
inputs = np.random.random((timesteps, input_features))

# 初始状态：全零向量
state_t = np.zeros((output_features,))

# (本行及以下2行)创建随机的权重矩阵
W = np.random.random((output_features, input_features))

U = np.random.random((output_features, output_features))

b = np.random.random((output_features,))
successive_outputs = []

# 对输入和当前状态（上一个输出）进行计算，得到当前输出。这里使用tanh来添加非线性（也可以使用其他激活函数）
for input_t in inputs:
    # input_t是形状为(input_features,)的向量
    output_t = np.tanh(np.dot(W, input_t) + np.dot(U, state_t) + b)

    # 将输出保存到一个列表中
    successive_outputs.append(output_t)

    # 更新网络状态，用于下一个时间步
    state_t = output_t

# 最终输出是形状为(timesteps, output_features)的2阶张量
final_output_sequence = np.stack(successive_outputs, axis=0)

RNN实现起来很简单。总而言之，RNN是一个for循环，它重复使用循环上一次迭代的计算结果，仅此而已。当然，你可以构建不同的RNN，它们都能满足上述定义。这个例子展示的只是最简单的RNN。RNN的特征在于时间步函数，比如本例中的下面这个函数，如下图所示：

output_t = np.tanh(np.dot(W, input_t) + np.dot(U, state_t) + b)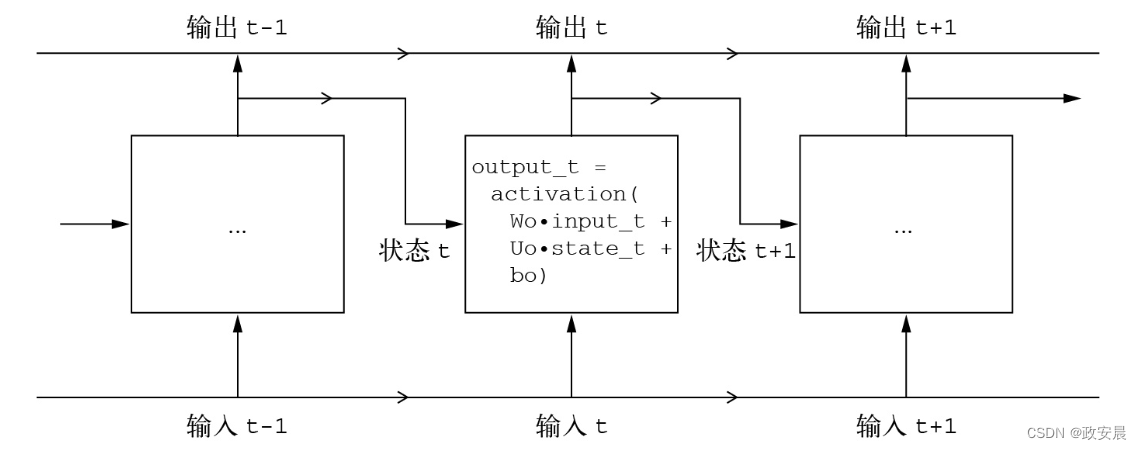

（一个简单的RNN，沿时间展开）

注意 本例的最终输出是一个形状为(timesteps, output_features)的2阶张量，其中每个时间步长是循环在t时间步长的输出。输出张量中的每个时间步t都包含入序列中时间步0到t的信息，即关于过去的全部信息。在多数情况下，你并不需要这个完整的输出序列，而只需要最后一个输出（循环结束时的output_t），因为它已经包含了整个序列的信息。

Keras中的循环层

上面的NumPy简单实现对应一个实际的Keras层——SimpleRNN层。

不过，二者有一点小区别：SimpleRNN层能够像其他Keras层一样处理序列批量，而不是像NumPy示例中的那样只能处理单个序列。也就是说，它接收形状为(batch_size, timesteps, input_features)的输入，而不是(timesteps, input_features)。指定初始Input()的shape参数时，你可以将timesteps设为None，这样神经网络就能够处理任意长度的序列，代码如下所示：

（能够处理任意长度序列的RNN层）

num_features = 14
inputs = keras.Input(shape=(None, num_features))
outputs = layers.SimpleRNN(16)(inputs)

如果你想让模型处理可变长度的序列，那么这就特别有用。但是，如果所有序列的长度相同，那么我建议指定完整的输入形状，因为这样model.summary()能够显示输出长度信息，这总是很好的，而且还可以解锁一些性能优化功能（以后文章咱们详述）。

Keras中的所有循环层（SimpleRNN层、LSTM层和GRU层）都可以在两种模式下运行：

一种是返回每个时间步连续输出的完整序列，即形状为(batch_size,timesteps, output_features)的3阶张量；

另一种是只返回每个输入序列的最终输出，即形状为(batch_size, output_features)的2阶张量。这两种模式由return_sequences参数控制。我们来看一个SimpleRNN示例，它只返回最后一个时间步的输出，代码如下所示：

（只返回最后一个时间步输出的RNN层）

num_features = 14
steps = 120
inputs = keras.Input(shape=(steps, num_features))

#  请注意，默认情况下使用return_sequences=False
outputs = layers.SimpleRNN(16, return_sequences=False)(inputs)

print(outputs.shape)

打印出的形状为 (None, 16)

还有，如下代码给出的示例返回了完整的状态序列（返回完整输出序列的RNN层）：

num_features = 14
steps = 120
inputs = keras.Input(shape=(steps, num_features))
outputs = layers.SimpleRNN(16, return_sequences=True)(inputs)
print(outputs.shape)

打印出的形状为 (None, 120, 16)

为了提高神经网络的表示能力，有时将多个循环层逐个堆叠也是很有用的。在这种情况下，你需要让所有中间层都返回完整的输出序列，代码如下所示：

RNN层堆叠

inputs = keras.Input(shape=(steps, num_features))
x = layers.SimpleRNN(16, return_sequences=True)(inputs)
x = layers.SimpleRNN(16, return_sequences=True)(x)
outputs = layers.SimpleRNN(16)(x)

我们在实践中很少会用到SimpleRNN层。

它通常过于简单，没有实际用途。特别是SimpleRNN层有一个主要问题：在t时刻，虽然理论上来说它应该能够记住许多时间步之前见过的信息，但事实证明，它在实践中无法学到这种长期依赖。原因在于梯度消失问题，这一效应类似于在层数较多的非循环网络（前馈网络）中观察到的效应：随着层数的增加，神经网络最终变得无法训练。Yoshua Bengio等人在20世纪90年代初研究了这一效应的理论原因。

oshua Bengio, Patrice Simard, Paolo Frasconi. Learning Long-Term Dependencies with Gradient Descent Is Difficult. IEEE Transactions on Neural Networks 5, no. 2, 1994.

值得庆幸的是，SimpleRNN层并不是Keras中唯一可用的循环层，还有另外两个：LSTM层和GRU层，二者都是为解决这个问题而设计的。

我们来看LSTM层，其底层的长短期记忆（LSTM）算法由Sepp Hochreiter和Jürgen Schmidhuber在1997年开发，是二人研究梯度消失问题的重要成果。

Sepp Hochreiter, Jürgen Schmidhuber. Long Short-Term Memory. Neural Computation 9, no. 8, 1997.

LSTM层是SimpleRNN层的变体，它增加了一种携带信息跨越多个时间步的方式。

假设有一条传送带，其运行方向平行于你所处理的序列。

序列中的信息可以在任意位置跳上传送带，然后被传送到更晚的时间步，并在需要时原封不动地跳回来。

这其实就是LSTM的原理：保存信息以便后续使用，从而防止较早的信号在处理过程中逐渐消失。

为了详细解释LSTM，我们先从SimpleRNN单元开始讲起，如下图所示：

因为有许多个权重矩阵，所以对单元中的W和U两个矩阵添加下标字母o（Wo和Uo），表示输出（output）。

（讨论LSTM层的出发点：SimpleRNN层）

我们向上图中添加新的数据流，其中携带跨越时间步的信息。这条数据流在不同时间步的值称为c_t，其中c表示携带（carry）。这些信息会对单元产生以下影响：它将与输入连接和循环连接进行计算（通过密集变换，即与权重矩阵做点积，然后加上偏置，再应用激活函数），从而影响传递到下一个时间步的状态（通过激活函数和乘法运算）。从概念上来看，携带数据流可以调节下一个输出和下一个状态，如下图所示。到目前为止，内容都很简单。

（从SimpleRNN到LSTM：添加携带数据流）

下面来看一下这种方法的精妙之处，即携带数据流下一个值的计算方法。

它包含3个变换，这3个变换的形式都与SimpleRNN单元相同，如下所示：

y = activation(dot(state_t, U) + dot(input_t, W) + b)

但这3个变换都有各自的权重矩阵，我们分别用字母i、f、k作为下标。目前的模型如下代码所示：

（LSTM架构的详细伪代码（1/2））

output_t = activation(dot(state_t, Uo) + dot(input_t, Wo) + dot(c_t, Vo) + bo)
i_t = activation(dot(state_t, Ui) + dot(input_t, Wi) + bi)
f_t = activation(dot(state_t, Uf) + dot(input_t, Wf) + bf)
k_t = activation(dot(state_t, Uk) + dot(input_t, Wk) + bk)

通过对i_t、f_t和k_t进行计算，我们得到了新的携带状态（下一个c_t），如下代码所示：

（LSTM架构的详细伪代码（2/2））

c_t+1 = i_t * k_t + c_t * f_t

添加上述内容之后的模型如下图所示。这就是LSTM层，不算很复杂，只是稍微有些复杂而已。

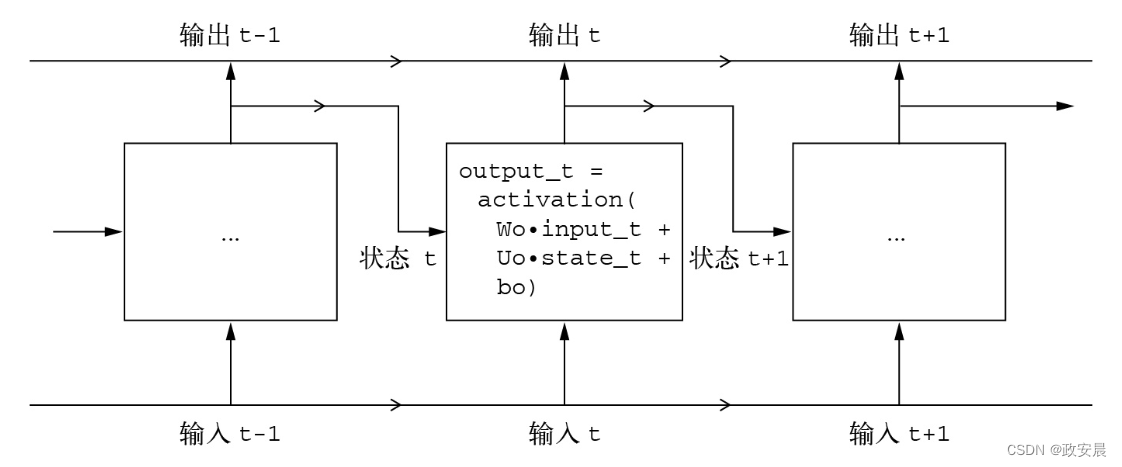
（详解LSTM架构）

你可以解释每个运算的作用。

比如你可以说，将c_t和f_t相乘，是为了故意遗忘携带数据流中不相关的信息。

同时，i_t和k_t都包含关于当前时间步的信息，可以用新信息来更新携带数据流。

但归根结底，这些解释并没有多大意义，因为这些运算的实际效果是由权重参数决定的，而权重以端到端的方式进行学习，每次训练都要从头开始，因此不可能为某个运算赋予特定的意义。

RNN单元的类型（如前所述）决定了假设空间，即在训练过程中搜索良好模型配置的空间，但它不能决定RNN单元的作用，那是由单元权重来决定的。

相同的单元具有不同的权重，可以起到完全不同的作用。因此，RNN单元的运算组合最好被解释为对搜索的一组约束，而不是工程意义上的设计。

这种约束的选择（如何实现RNN单元）最好留给优化算法来完成（比如遗传算法或强化学习过程），而不是让人类工程师来完成。那将是未来我们构建模型的方式。

总之，你不需要理解LSTM单元的具体架构。作为人类，你不需要理解它，而只需记住LSTM单元的作用：允许过去的信息稍后重新进入，从而解决梯度消失问题。

---