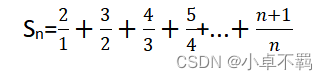神经网络实战前言

应用广泛

从人脸识别到网约车，在生活中无处不在

未来可期

无人驾驶技术便利出行
医疗健康改善民生

产业革命

第四次工业革命——人工智能

机器学习概念

机器学习不等价与人工智能
20世纪50年代，人工智能是说机器模仿人类行为的能力

符号人工智能

基于符号，将人类的知识声明为一种计算机可以处理的形式
专家系统发展于人工智能
模拟人类的决策
缺点是：依赖人类专家的知识，解决问题的规则和认知是被编程的

机器学习

通俗讲，机器从已有的数据中学习并对其他数据做预测

机器学习的基础条件

海量的数据存储能力
强大的运算能力

刚开始科学家使用符号人工智能，但是发现研究进展不顺，随着计算机硬件的提升，机器学习的基础条件得到满足后，AI发展迎来春天。

机器学习算法

有监督分类

标记过的训练数据
学习从输入变量映射到目标变量的规则
例如：降雨（目标变量），温度、时间、气压、风速等等就是输入变量

无监督分类

未经标记过的训练数据
学习数据中的关联规则、模式及类别
常见案例是聚类分析

监督分类的案例

区分两种动物，兔子和大象
收集到的数据有速度和体重
兔子的特征是，体重小，速度快
大象的特征是，体重大，速度慢
机器学习算法的任务就是，找到分割兔子和大象的区别，生成决策边界线，将海量的数据一分为二，线就是决策边界。
有了决策边界，就可以对未知的数据集进行预测，判断类型
不同的学习算法会对最终的结果有影响

常用的机器学习方法包括：

神经网络
线性回归
对数概率回归
支持向量机
决策树

机器学习的工作流程

输入数据
1. 多个数据源
数据预处理
1. 数据整合
2. 数据编码
3. 数据换算和标准化
4. 补充缺失数据
  1. 均值替换缺失值
  2. 基于存在数据预测缺失值
5. 训练测试数据分割
数据分析
1. 数据可视化
2. 探索性数据分析
  1. 特征工程
  2. 领域知识加入机器学习
模型构建
1. 选择学习模型
2. 调参
3. 训练模型
4. 评估模型
输出结果
1. 输出未知数据集的预测结果

神经网络

模拟人类大脑神经元

单层神经网络——感知机

核心：数学函数
过程：输入+运算+输出

为什么神经网络好？

通用函数逼近器

现实生活中的问题总能用数学函数来表征，不论函数有多复杂，神经网络都能对这个函数无限逼近（前提：理想的算力）

可扩展性好且灵活

神经网络的不同堆叠方式和排列组合可以解决各种问题，好的程序员对网络的编排更为熟悉。

神经网络的内部工作原理

输入层
一个或者多个的隐藏层
输出层
每层之间包含权重W和偏差b
为每个隐藏层所选择的激活函数σ

Python中训练神经网络

import numpy as np

class NeuralNetwork:
    def__init__(self,x,y):
        self.input=x
        self.weights1=np.random.rand(self.input.shape[1],4)
        self.weights2=np.random.rand(4,1)
        self.y=y
        self.output=np.zeros(self.y.shape)

import numpy as np：导入NumPy库并将其重命名为np，用于处理数组和矩阵等数学运算。
class NeuralNetwork:：定义了一个名为NeuralNetwork的类，用于表示神经网络。
def __init__(self, x, y):：定义了类的构造函数，用于初始化神经网络的参数。
self.input = x：将输入数据x保存到类的属性input中。
self.weights1 = np.random.rand(self.input.shape[1], 4)：随机初始化输入层到隐藏层之间的权重矩阵，矩阵大小为输入数据的特征数（x的列数）乘以隐藏层的神经元数（这里设定为4）。
self.weights2 = np.random.rand(4, 1)：随机初始化隐藏层到输出层之间的权重矩阵，矩阵大小为隐藏层的神经元数（4）乘以输出值。
self.y = y：将输出数据y保存到类的属性y中。
self.output = np.zeros(self.y.shape)：初始化一个和输出数据y相同大小的零矩阵，用于保存神经网络的输出值。

两层神经网络的数学内核

$\hat{y} = \sigma\left[W_2\sigma(W_1x + b_1) + b_2\right]$

其中：
$x$ 是输入向量，
$W_1$ 是第一个隐藏层的权重矩阵， $b_1$ 是第一个隐藏层的偏置向量，
$\sigma$ 是激活函数（如 Sigmoid 函数），
$W_2$ 是第二个隐藏层到输出层的权重矩阵， $b_2$ 是输出层的偏置向量，
$\hat{y}$ 是神经网络的输出向量。

神经网络的训练包括2个步骤

前馈：计算预测输出 $\hat{y}$
反向传播（Backward Propagation）：更新权重和偏差

前馈

进行前向传播计算，假设偏差都为0

import numpy as np

class NeuralNetwork:
    def__init__(self,x,y):
        self.input=x
        self.weights1=np.random.rand(self.input.shape[1],4)
        self.weights2=np.random.rand(4,1)
        self.y=y
        self.output=np.zeros(self.y.shape)
    def feedforward(self):
        self.layer1=sigmoid(np.dot(self.input,self.weights1))
        self.layer2=sigmoid(np.dot(self.input,self.weights2))

1. `self.layer1 = sigmoid(np.dot(self.input, self.weights1))`：将输入数据 `self.input` 与第一层的权重矩阵 `self.weights1` 相乘，并通过 Sigmoid 激活函数进行非线性变换，得到第一层的输出 `self.layer1`。这一步表示输入数据经过第一层的处理后的输出。

2. `self.layer2 = sigmoid(np.dot(self.input, self.weights2))`：将输入数据 `self.input` 与第二层的权重矩阵 `self.weights2` 相乘，并通过 Sigmoid 激活函数进行非线性变换，得到第二层的输出 `self.layer2`。这一步表示第一层的输出经过第二层的处理后的输出。

这段代码的目的是计算神经网络的前向传播过程中各层的输出，以便后续计算损失函数和进行反向传播更新权重。值得注意的是，这里的 `sigmoid` 函数是一个自定义的激活函数，用于将神经网络的输出限制在0到1之间。

损失函数

损失函数有多种，目前以平方和误差为例

$SSE = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2$

平方和误差就是对实际值和预测值之间的差值求和

目标是实现训练神经网络并找到是损失函数最小化的最优权重

反向传播

计算出预测结果的误差（损失），需要找到一种方法将误差在网络中反向传导以便更新权重和偏差。

要找合适的权重和偏差矫正量，需要知道损失函数关于权重及偏差的导数

函数的导数就是函数的斜率

根据导数就可以根据导数的值增加或者减少导数值的方式来调节权重和偏差，这种方法也称为梯度下降法

使用链式法则求损失函数的导数，链式法则封装在keras等机器学习的库中

关键点：由损失函数关于权重的导数（斜率），帮助调整权重

import numpy as np

def sigmoid(x):
    return 1.0/(1+np.exp(-x))
def sigmoid_derivative(x):
    return x*(1.0-x)
class NeuralNetwork:
    def __init__(self,x,y):
        self.input=x
        self.weights1=np.random.rand(self.input.shape[1],4)
        self.weights2=np.random.rand(4,1)
        self.y=y
        self.output=np.zeros(self.y.shape)
    def feedforward(self):
        self.layer1=sigmoid(np.dot(self.input,self.weights1))
        self.output =sigmoid(np.dot(self.layer1,self.weights2))
    def backprop(self):
        #Find the derivative of the loss function with respect to weight2 and weight1 using the chain rule
        d_weights2=np.dot(self.layer1.T,(2*(self.y-self.output)*sigmoid_derivative(self.output)))
        d_weights1=np.dot(self.input.T,(np.dot(2*(self.y-self.output)*sigmoid_derivative(self.output),self.weights2.T)*sigmoid_derivative(self.layer1)))
        self.weights1 +=d_weights1
        self.weights2 +=d_weights2
if __name__=="__main__":
    X=np.array([[0,0,1],
               [0,1,1],
               [1,0,1],
               [1,1,1]])
    y=np.array([[0],[1],[1],[0]])
    nn=NeuralNetwork(X,y)
    
    for i in range(1500):
        nn.feedforward()
        nn.backprop()
    print(nn.output)

这段代码实现了一个简单的神经网络，包括一个输入层、一个隐藏层和一个输出层。以下是每个模块的描述：

import numpy as np: 导入NumPy库，用于处理数组和矩阵等数值计算。
def sigmoid(x): 定义sigmoid激活函数，用于将输入值转换为0到1之间的值。
def sigmoid_derivative(x): 定义sigmoid激活函数的导数，用于反向传播中计算梯度。
class NeuralNetwork: 定义神经网络类，包括初始化方法__init__、前向传播方法feedforward和反向传播方法backprop。
- __init__(self, x, y): 初始化神经网络，包括输入数据x、目标输出y、第一层到第二层的权重weights1和第二层到输出层的权重weights2。
- feedforward(self): 执行神经网络的前向传播，计算输入经过权重后得到的输出。
- backprop(self): 执行神经网络的反向传播，根据损失函数的梯度更新权重，以减小预测输出与实际输出之间的差距。
if __name__=="__main__":：主程序入口，创建神经网络对象并进行训练。
- 创建输入数据X和目标输出y。
- 创建神经网络对象nn。
- 循环执行1500次训练迭代，每次迭代包括前向传播和反向传播。
- 打印训练后的输出结果nn.output。

重要点：Sigmoid是激活函数，将函数值压缩到0~1，对于二元问题，就是将预测结果位于0~1

结果精度检验

x1	x2	x3	Y
0	0	1	0
0	1	1	1
1	0	1	1
1	1	1	0

迭代神经网络1500次，给出了最后的预测结果，与真实值进行对照，同时给出损失迭代-次数图

if __name__=="__main__":
    X=np.array([[0,0,1],
               [0,1,1],
               [1,0,1],
               [1,1,1]])
    y=np.array([[0],[1],[1],[0]])
    nn=NeuralNetwork(X,y)

    losses = []  # 用于记录每次迭代后的损失值

    for i in range(1500):
        nn.feedforward()
        nn.backprop()
        loss = np.mean(np.square(nn.y - nn.output))  # 计算均方误差损失
        losses.append(loss)

    plt.plot(range(1, 1501), losses)  # 绘制损失-迭代次数图
    plt.xlabel('Iterations')
    plt.ylabel('Loss')
    plt.title('Loss vs. Iterations')
    plt.show()

为什么要求平均，不平均代码报错？

在计算损失时，我们通常会计算所有样本的损失值的平均值。这是因为损失是所有样本预测值与真实值之间差值的函数，我们希望损失值能够反映整个数据集的预测准确程度，而不仅仅是单个样本的准确程度。因此，对所有样本的损失值取平均可以更好地衡量整个模型的性能。

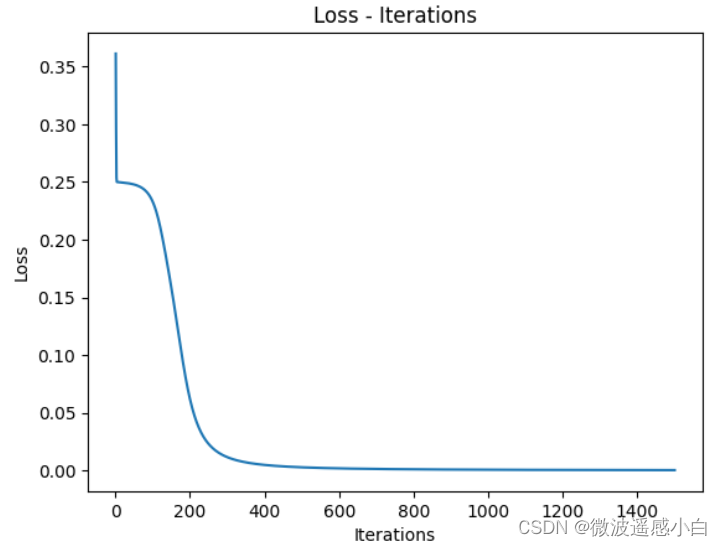
预测值	实际值
0.00924	0
0.97257	1
0.97201	1
0.03434	0

由图片和图表可以看出来，前馈和反向传播算法成功训练的神经网络，且预测值收敛于真实值，且预测值与真实值有一定的误差，这个是在允许范围之内的。

最后

    for i in range(1500):
        nn.feedforward()
        nn.backprop()
        loss = np.mean(np.square(nn.y - nn.output))  # 计算均方误差损失
        losses.append(loss)

这块代码可以在类中进行分装，代码简洁，迁移性、可读性好

def train(self, epochs):
        for i in range(epochs):
            self.feedforward()
            self.backprop()
            loss = np.mean(np.square(self.y - self.output))  # 计算均方误差损失
            self.losses.append(loss)
if __name__=="__main__":
    X=np.array([[0,0,1],
               [0,1,1],
               [1,0,1],
               [1,1,1]])
    y=np.array([[0],[1],[1],[0]])
    nn=NeuralNetwork(X,y)
    
    nn.train(1500)  # 进行1500次训练迭代
    
    plt.plot(range(1, 1501), nn.losses)  # 绘制损失-迭代次数图
    plt.xlabel('Iterations')
    plt.ylabel('Loss')
    plt.title('Loss - Iterations')
    plt.show()