LCR 112. 矩阵中的最长递增路径

给定一个 m x n 整数矩阵 matrix ，找出其中 最长递增路径 的长度。

对于每个单元格，你可以往上，下，左，右四个方向移动。 不能 在 对角线 方向上移动或移动到 边界外（即不允许环绕）。

示例 1：

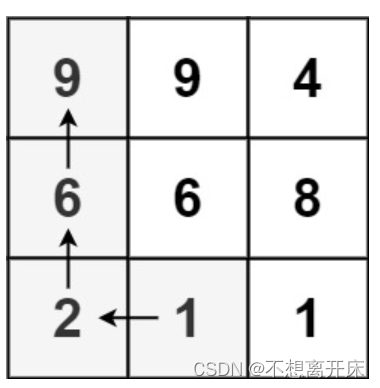
输入：matrix = [[9,9,4],[6,6,8],[2,1,1]]
输出：4
解释：最长递增路径为 [1, 2, 6, 9]。

示例 2：

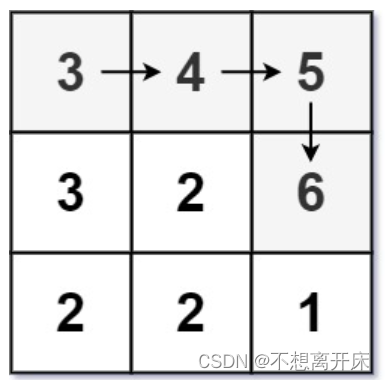
输入：matrix = [[3,4,5],[3,2,6],[2,2,1]]
输出：4
解释：最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。

示例 3：
输入：matrix = [[1]]
输出：1

提示：
m == matrix.length
n == matrix[i].length
1 <= m, n <= 200
0 <= matrix[i][j] <= 231 - 1

dfs+记忆化搜索

dp[i][j]表示以matrix[i][j]为出发点的最长递增路径

class Solution {
public:
    int res=0;
    int dp[205][205];
    int dfs(vector<vector<int>>& matrix,int m,int n,int x,int y)
    {
        //如果dp[x][y]不为0，则表示已经有记录，直接返回长度
        if(dp[x][y]) return dp[x][y];
        if(x+1<m&&matrix[x+1][y]>matrix[x][y]) dp[x][y]=max(dp[x][y],dfs(matrix,m,n,x+1,y)+1);
        if(y+1<n&&matrix[x][y+1]>matrix[x][y]) dp[x][y]=max(dp[x][y],dfs(matrix,m,n,x,y+1)+1);
        if(x-1>=0&&matrix[x-1][y]>matrix[x][y]) dp[x][y]=max(dp[x][y],dfs(matrix,m,n,x-1,y)+1);
        if(y-1>=0&&matrix[x][y-1]>matrix[x][y]) dp[x][y]=max(dp[x][y],dfs(matrix,m,n,x,y-1)+1);
        return dp[x][y];
    }
    int longestIncreasingPath(vector<vector<int>>& matrix) 
    {
        int m=matrix.size();
        int n=matrix[0].size();
        //遍历每个点
        for(int i=0;i<m;i++)
        {
            for(int j=0;j<n;j++)
            {
                res=max(res,dfs(matrix,m,n,i,j));
            }
        }
        return res+1;
    }
};