在量化金融股市市场中,因子有效性的检验是经常被提及的。实际上对于多因子量化选股模型的有效性分析,更有指导参考意义的指标应该观察看的IC和IR。
因子评价4大维度:
1.因子单调性:因子单调性越高,收益越强。
2.因子有效性:因子对未来收益的解释能力。
3.因子稳定性:因子的有效性是否稳定、可持续。
4.因子时效性:在过去有效的因子,现在或将来不一样有效。
▍信息系数IC介绍
表示所选股票的因子值与股票下期收益率的截面相关系数,通过 IC 值可以判断因子值对下期收益率的预测能力。通俗来说,IC代表因子选股带来的超额收益能力。IC值越大,因子的Alpha就越大:
1.IC的最大值为1,则因子预测能力100%准确;
2.IC最小值为-1,则因子反向的预测作用;
3.IC等于0,则因子预测无效果;
4.当IC大于5%或者小于-5%,就认为因子是比较有效。
5.如果IC的平均值能够达到10%以上,则代表这个因子的预测能力非常强。
常见的IC有两种:一种是Normal IC 另外一种则是Rank IC。通常使用的是RankIC,此时IC表示因子选出股票的排名与股票收益率的相关性。
-
Normal IC
IC的定义:t期(这里的期一般指的是调仓周期)的因子载荷(因子值)对t+1期的收益预测值和实际收益之间的相关系数。
-
Rank IC
Rank IC即某时点某因子在全部股票暴露值排名与其下期回报排名的截面相关系数,它与IC的区别就是将因子的具体值以及收益的具体值都转换为了所对应的数值在其截面上的排序名次。然后通过计算排序值的相关系数(秩相关系数),得到Rank IC。
具体案例方法:
第一种方法是按照因子取值把个股分成 n 档(比如6档),然后将每一档视作一个投资组合,计算投资组合收益率和投资组合因子在截面上的 IC 或 Rank IC。每一个投资组合中,可以按照等权或者市值加权来计算投资组合的收益率和因子取值。因子描述的是一揽子股票所共同承担(或者暴露于的)的某一方面的系统性风险。使用因子选股是为了规避个股特异性收益率的风险。因此,比起个股,我们更应该关注一揽子股票的收益率和相应因子取值之间的相关性。这就是使用因子构建投资组合、再计算 IC 的初衷。投资组合的收益率是一揽子股票的均值,也可以更好地消除收益率上的噪音。
▍信贷风控角度计量IC值
将分箱坏账率作为投资组合的收益率,按照信贷风控中征信指标或者外部数据评分取值把所有客户同一时间段的样本分成 n 档(比如6档),然后将每一档视作一个分箱组合,计算分箱组合坏账率和分箱组合因子在截面上的 IC 或 Rank IC。每一个分箱组合中,可以按照等权或者平均加权来计算分箱组合的坏账率和因子取值。
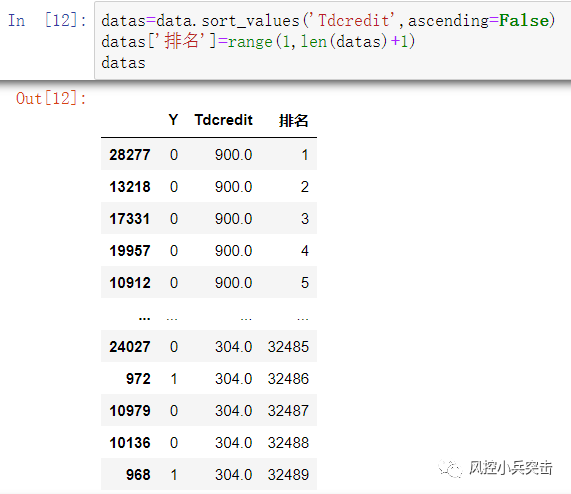
d1 = pd.DataFrame({'x':datas['Tdcredit'],'y':datas['Y'],'bucket':pd.cut(datas['Tdcredit'],6)}) #利用pd.cut实现等距分箱
d2 = d1.groupby('bucket',as_index=True) # 按照分箱结果进行分组聚合
d3 = pd.DataFrame(d2.x.min(),columns=['min_bin'])
d3['min_bin'] = d2.x.min() # 箱体的左边界
d3['max_bin'] = d2.x.max() # 箱体的右边界
d3['mean_bin']=d2.x.mean()
d3['bad'] = d2.y.sum() # 每个箱体中坏样本的数量
d3['total'] = d2.y.count() # 每个箱体的总样本数
d3['bad_rate'] = d3['bad']/d3['total'] #
d3['分组']=range(1,len(d3)+1)
d3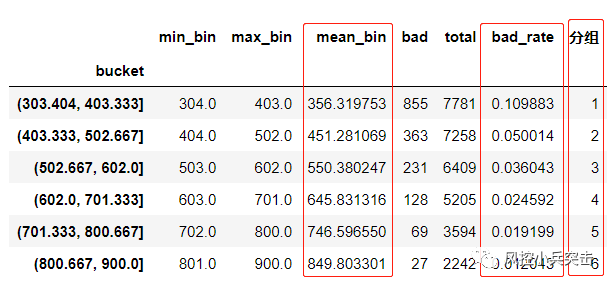
通过计算因子排名与分组坏账率计算IC值和计算因子分组平均值与分组坏账率计算IC值:
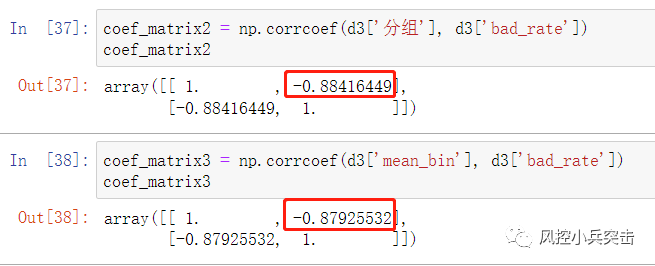
第二种方法仍然从分组坏账率和因子取值的 IC 出发,但是在计算时根据因子的业务逻辑(大到小、还是小到大的关系)来给 x 和 y 的取值赋权,从而得到weighted IC。由于结合了从业务逻辑出发的权重,这个加权 IC 能更好的反映因子的选股能力。
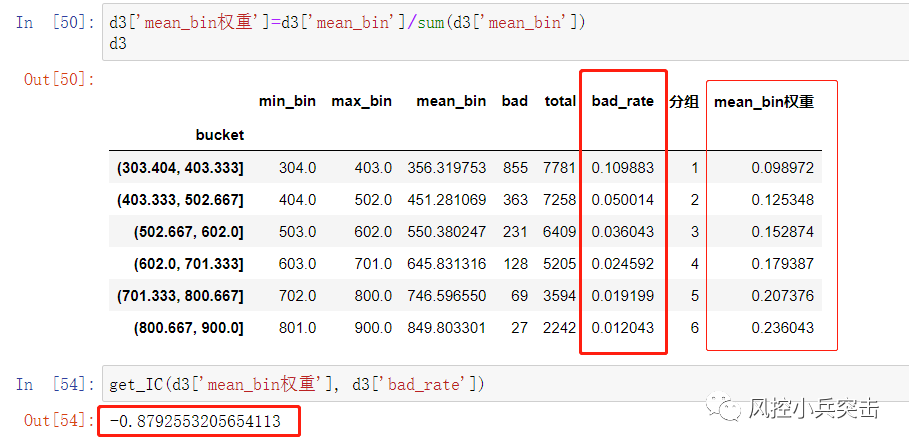
总结:通过两种方法去计量IC值,绝对值均大于0.8。可知该因子的筛选坏客户的能力很强。好坏区分能力效能很好。IC_IR:IC / IC的标准差,衡量因子IC的稳定性。p-value:衡量因子与未来坏账率相关度的显著性,通常我们认为 p-value 低于0.05 的因子对未来坏账率有预测性。也要去考察因子的稳定性,不同时间段的IC值是否稳定和正负方向是否稳定。