1. LC56 合并区间
题目链接
- Arrays.sort先让intervals里的子数组按照子数组的第一个数字值从小到大排列。
- 开一个新数组,newInterval,存放合并好的子数组
- 让intervals的当前子数组i的第一个数字与newInterval的当前子数组index的最后一个数字比较大小:如果区间没有重叠,则interval的i加入newInterval; 如果重叠,则与newInterval的区间合并
- 注意合并时,并不是newInterval[index][1] = intervals[i][1];
而是newInterval[index][1] = Math.max(newInterval[index][1], intervals[i][1]);
因为有可能是这种情况:[1,6],[2,4]——这种情况合并还是[1,6]。

秒懂力扣区间题目:重叠区间、合并区间、插入区间
class Solution {
public int[][] merge(int[][] intervals) {
Arrays.sort(intervals, (v1, v2) -> v1[0] - v2[0]);
int[][] newInterval = new int[intervals.length][2];
newInterval[0] = intervals[0];
int index = 0;
for (int i=1; i<intervals.length; i++){
if (intervals[i][0] > newInterval[index][1]){
index++;
newInterval[index] = intervals[i];
}else{
newInterval[index][1] = Math.max(newInterval[index][1], intervals[i][1]);
}
}
return Arrays.copyOf(newInterval, index+1);
}
}
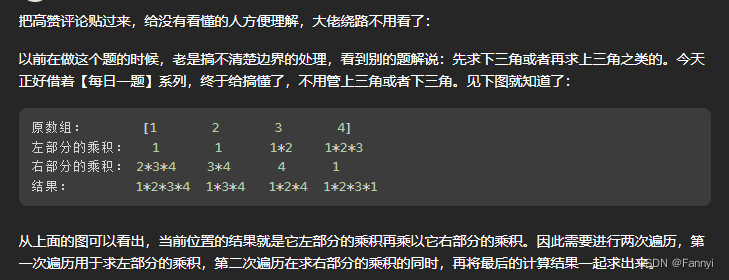
2. LC238除自身以外数组的乘积
题目链接
class Solution {
public int[] productExceptSelf(int[] nums) {
int[] left = new int[nums.length];
int[] right = new int[nums.length];
//left
left[0] = 1;
for (int i=1; i<left.length; i++){
left[i] = left[i-1] * nums[i-1];
}
//right
right[right.length-1] = 1;
for (int i=right.length-2; i>=0; i--){
right[i] = right[i+1] * nums[i+1];
}
//合并
int[] result = new int[nums.length];
for (int i=0; i<nums.length; i++){
result[i] = left[i] * right[i];
}
return result;
}
}
3.随想录1、二分查找
题目链接
最重要的是确定左闭右闭区间,所以while条件是<=。因为左闭右闭就是左边区间也包括,右边区间也包括,所以左右区间可以=。如果是开区间,一个区间不包括,一个区间包括,那么两个区间必不能相等。
代码
class Solution {
public int search(int[] nums, int target) {
int left = 0;
int right = nums.length-1;
// 避免当 target 小于nums[0] nums[nums.length - 1]时多次循环运算
if (target < nums[0] || target > nums[nums.length - 1]) {
return -1;
}
while(left <= right){
int mid = (right+left)/2;
if (nums[mid] == target){
return mid;
}
else if (nums[mid] > target){
right = mid - 1;
}
else if (nums[mid] < target){
left = mid + 1;
}
}
return -1;
}
}
4. LC560 和为k的子数组
题目链接
解法一:
暴力算法
易错:在外层循环时,nums[i] == k了之后不要continue,还有继续内循环。因为可能会有这种情况:满足和为k之后,后面出现了1和-1。此时相加和依然为k。
class Solution {
public int subarraySum(int[] nums, int k) {
int sum = 0;
int count = 0;
for (int i=0; i<nums.length; i++){
sum = nums[i];
if (nums[i] == k){
count++;
}
for (int j=i+1; j<nums.length; j++){
sum += nums[j];
if (sum == k){
count++;
}
}
}
return count;
}
}
解法二:
前缀和
假设数组的前缀和数组为prefixSum,其中prefixSum[i]表示从数组起始位置到第i个位置的元素之和。
对于任意的两个下标i和j(i < j),如果prefixSum[j] - prefixSum[i] = k,即从第i个位置到第j个位置的元素之和等于k,那么说明从第i+1个位置到第j个位置的连续子数组的和为k。
遍历数组,计算每个位置的前缀和,并使用一个哈希表来存储每个前缀和出现的次数。在遍历的过程中,检查是否存在prefixSum[j] - k的前缀和,如果存在,说明从某个位置到当前位置的连续子数组的和为k,将对应的次数累加到结果中。
这样,通过遍历一次数组,统计出和为k的连续子数组的个数,并且时间复杂度为O(n),其中n为数组的长度。
class Solution {
public int subarraySum(int[] nums, int k) {
int preSum = 0;
int count = 0;
Map<Integer, Integer> map = new HashMap<>();
map.put(0,1); // 初始化前缀和为0的次数为1
for (int i=0; i<nums.length; i++){
preSum += nums[i];
if (map.containsKey(preSum-k)){
count += map.get(preSum-k);
}
if (map.containsKey(preSum)){
map.put(preSum, map.get(preSum)+1);
}else{
map.put(preSum, 1);
}
}
return count;
}
}
!!为什么要初始化前缀和?
如果从数组的开始位置到当前位置的子数组的和恰好等于 k,那么这个子数组的前缀和就是 0,即 sum - k 等于 0。因此,需要初始化一个前缀和为 0 的次数为 1,表示从数组的开始位置到当前位置的子数组的和为 k 的情况。如果不初始化,那么这种情况会被漏掉,导致结果不正确。