回溯算法套路③排列型回溯+N皇后【基础算法精讲 16】

news2024/10/6 5:58:46

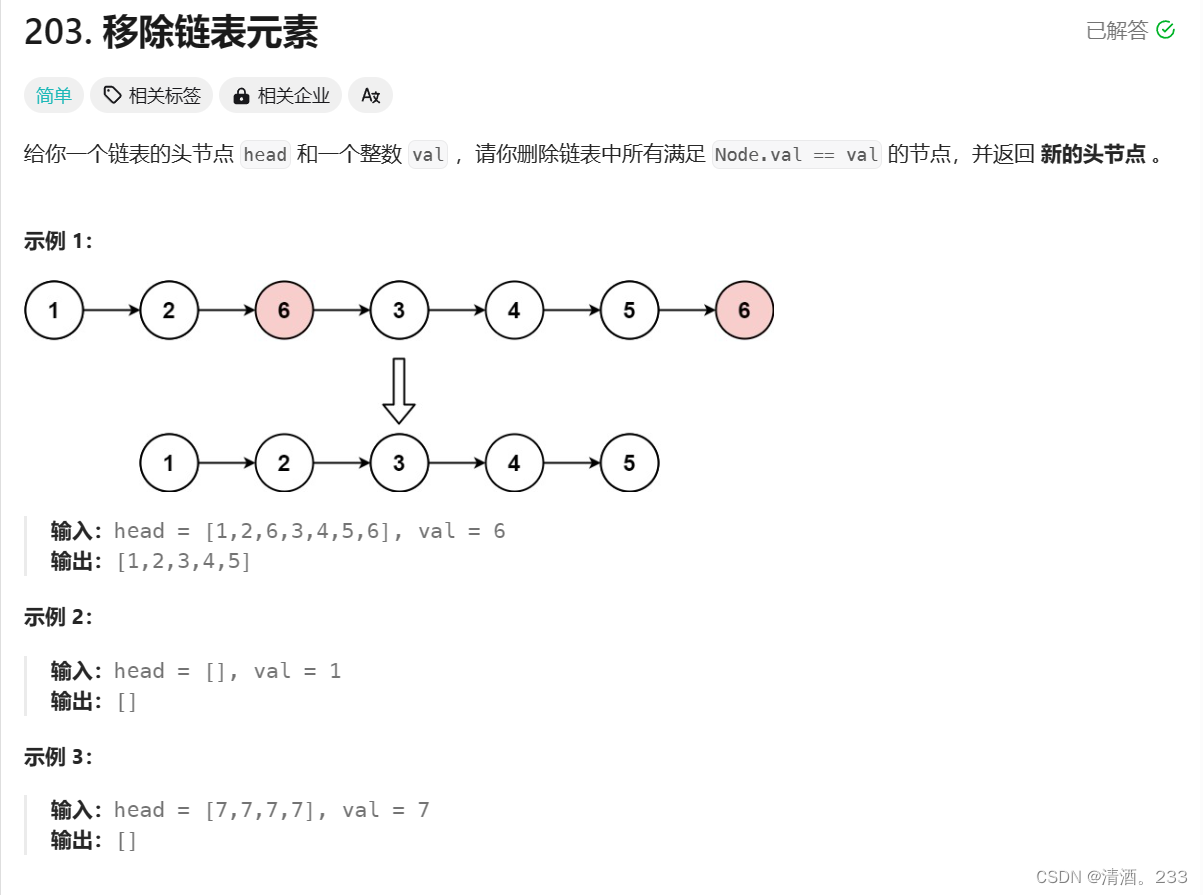
46 . 全排列

链接 :

. - 力扣（LeetCode）

思路 :

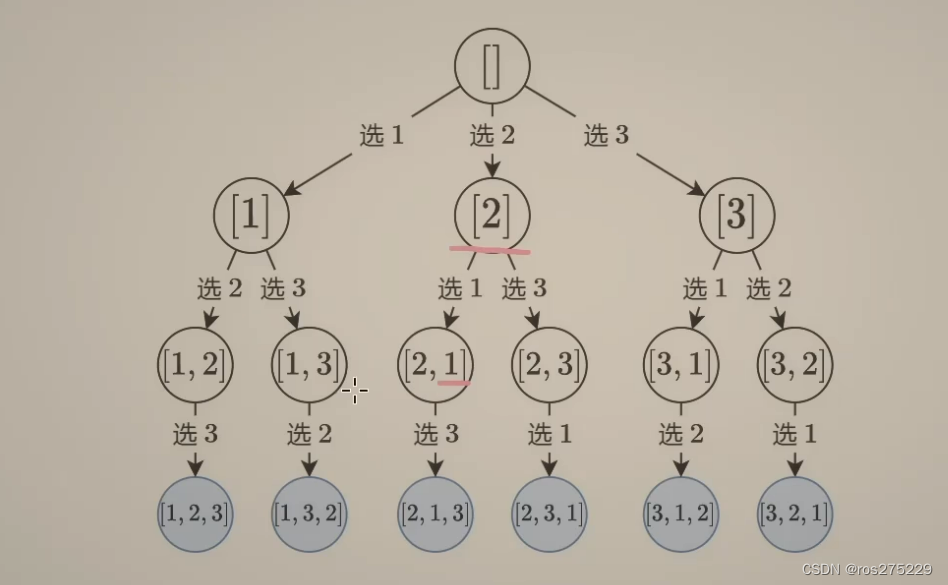
那么怎么确定选了那个数呢?

这里设置一个used表示i选没选过 ;

class Solution {
public:
    vector<vector<int>> ans;
    vector<int> path;
    void backtrack(vector<int>nums,vector<bool> used){
        if(path.size() >= nums.size()){
            ans.push_back(path);
            return;
        }
        for(int i=0;i<nums.size();i++){
            if(used[i]==true) continue;
            used[i] = true;
            path.push_back(nums[i]);
            backtrack(nums,used);
            used[i] = false;
            path.pop_back();
        }
    }
    vector<vector<int>> permute(vector<int>& nums) {
        ans.clear();
        path.clear();
        vector<bool> used(nums.size(),false);
        backtrack(nums,used);
        return ans;
    }
};

51 . N皇后

链接 :

. - 力扣（LeetCode）

思路 :

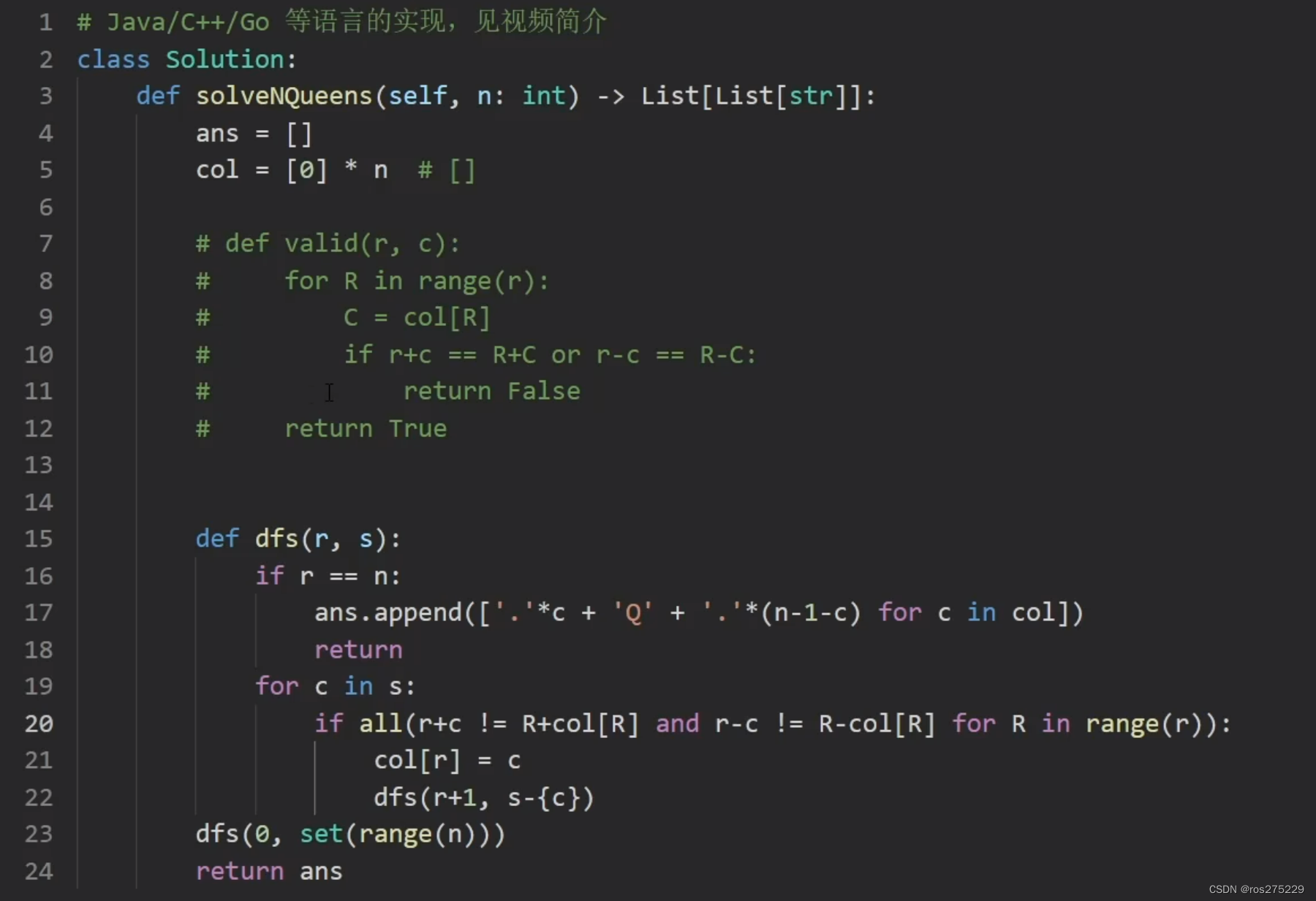
class Solution {
public:
    vector<vector<string>> solveNQueens(int n) {
        vector<vector<string>> ans;
        vector<int> col(n), on_path(n), diag1(n * 2 - 1), diag2(n * 2 - 1);
        function<void(int)> dfs = [&](int r) {
            if (r == n) {
                vector<string> board(n);
                for (int i = 0; i < n; ++i)
                    board[i] = string(col[i], '.') + 'Q' + string(n - 1 - col[i], '.');
                ans.emplace_back(board);
                return;
            }
            for (int c = 0; c < n; ++c) {
                int rc = r - c + n - 1;
                if (!on_path[c] && !diag1[r + c] && !diag2[rc]) {
                    col[r] = c;
                    on_path[c] = diag1[r + c] = diag2[rc] = true;
                    dfs(r + 1);
                    on_path[c] = diag1[r + c] = diag2[rc] = false; // 恢复现场
                }
            }
        };
        dfs(0);
        return ans;
    }
};

52. N 皇后 II

链接 :

. - 力扣（LeetCode）

思路 :

直接套用上一题代码,返回ans.size()即可 ;

代码 :

class Solution {
public:
    int totalNQueens(int n) {
        vector<vector<string>> ans;
        vector<int> col(n), on_path(n), diag1(n * 2 - 1), diag2(n * 2 - 1);
        function<void(int)> dfs = [&](int r) {
            if (r == n) {
                vector<string> board(n);
                for (int i = 0; i < n; ++i)
                    board[i] = string(col[i], '.') + 'Q' + string(n - 1 - col[i], '.');
                ans.emplace_back(board);
                return;
            }
            for (int c = 0; c < n; ++c) {
                int rc = r - c + n - 1;
                if (!on_path[c] && !diag1[r + c] && !diag2[rc]) {
                    col[r] = c;
                    on_path[c] = diag1[r + c] = diag2[rc] = true;
                    dfs(r + 1);
                    on_path[c] = diag1[r + c] = diag2[rc] = false; // 恢复现场
                }
            }
        };
        dfs(0);
        return ans.size();
    }
};