本文讨论了分布式数据库在在线扩容方面的挑战， 详细解释了一般分布式数据库和 TiDB 在扩容机制上的不同。 一般分布式数据库在进行在线扩容时，需要重新平衡数据分布，可能会影响系统的可用性和 IO 消耗。 相比之下，TiDB 的存算分离架构使得扩容对业务影响较小。

作者：爱喝自来水的猫 来源公众号：数据源的技术后花园。

昨天和别人交流 PingCAP TiDB 时，这位同学对“ TiDB 在线扩容对业务几乎没有影响 ” 这一点表示不太理解，惊讶 TiDB 到底是怎么做到的。 细聊下来，发现这位同学是一位主要负责集中式和早期分布式架构数据库的 DBA 人员，比较熟悉 Oracle、Greenplum。 于是我有点理解他的惊讶了，因为 Oracle 和 Greenplum 我也是有一点点经验，本文简单针对一般分布式数据库和 TiDB 在扩容机制上谈一点个人的理解。

一般分布式数据库在线扩容是怎么做的

集中式数据库因为其架构本身的限制，一般来说想要实现在线扩容是比较困难的，这里暂且不予讨论，我们主要了解一下一般分布式数据库的扩容是如何进行的。不管是 Greenplum 这种 MPP 数据库，还是其它的分库分表数据库，为了实现数据的均衡分布，通常需要在表上定义相关的分布键。通过分布键，再结合哈希算法，可以把数据哈希散列到不同的数据节点中，类似于 hash （ key ） % N （ key 代表分布键， N 代表数据节点编号） 。举个例子，假如一个分布式数据库有 3 个数据节点，表的分布键为 ID （ ID 是一个递增序列），那么基于哈希算法散列后数据的分布大致如下图所示：

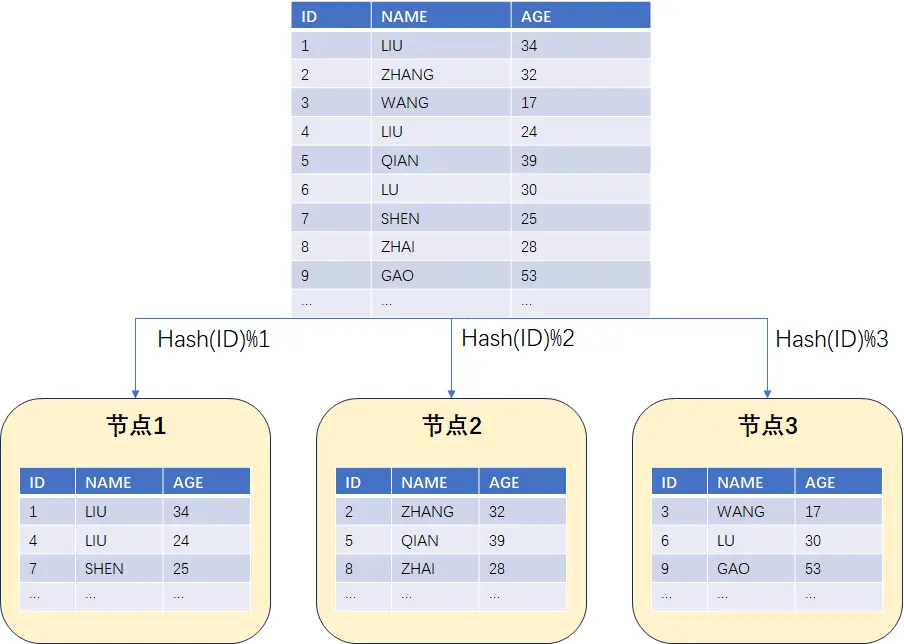
现在我们需要扩容一个节点，从原来的 3 节点扩容到 4 节点。为了保证原来哈希散列结果的一致性数据需要重新平衡，平衡后的数据分布应该如下面图中所示。可以发现，这个时候大部分的数据基本都搬迁了一遍。先不说数据的迁移是否对业务造成阻塞，光是这现有的大面积数据均衡足以导致整个系统的 IO 消耗极高， 严重影响整个系统的可用性。

Greenplum 在官方文档中还明确指出“ 正在被重新分布的表或者分区会被锁定并且不可读写。当其重新分布完成后，常规操作才会继续 ”。可以明确的说， Greenplum 早期版本里面根本就不 支持所谓的“ 在线 ”扩容。

时代在进步，数据库技术也在进步。为了尽可能实现在线扩容的能力， Greenplum 数据库包括其他的分库分表数据库开始引入一些新的算法来优化此事。 一致性哈希算法 开始被普遍应用，它与传统哈希算法最主要的不同是 不再使用节点编号来进行散列 ，而是使用 2^32 这样一个固定值做取模运算。一致性哈希算法将表中的数据和节点编号映射到一个圆环上，当增加节点时影响的数据范围只是圆环上的一小段数据范围。比如下图中增加节点 4 ，影响的数据只有节点 1 到节点 4 之间的这部分数据。

一致性哈希算法解决了数据重分布时大量数据搬迁的问题，减少了数据搬迁时的网络 IO 和磁盘 IO 。不过要真正实现不影响业务，还需要改进数据重分布内部的机制，比如 重分布时锁表 等问题。

TiDB 的扩容是怎么做的以及为什么它几乎不影响业务?

TiDB 的扩容机制离不开 TiDB 整体的架构实现。作为一个存算分离的原生分布式架构， TiDB 集群主要由三大模块构成：用于集群元数据管理及集群调度的 PD 、用于接收外部请求并解析编译执行 SQL 的计算引擎 TiDB Server 以及用于数据存储以及多副本数据一致性保证的存储引擎 TiKV/TiFlash。

基于存算分离的架构，TiDB 可以单独进行计算层扩容和存储层扩容。计算层的扩容相对简单，因为 TiDB Server 本身是无状态的。TiDB Server 节点不持久化数据，每个节点也是完全对等的，当 TiDB Server 计算资源不够了，只需要增加 TiDB Server 节点，然后修改上层的负载均衡组件将客户端连接均衡分发到新的 TiDB Server 节点即可（目前大多数负载均衡组件都支持动态修改配置）。因此，计算节点的扩容完全不会影响现有的业务。

针对存储节点， TiKV 的扩容与一般分布式数据库的扩容机制是完全不同的，这主要因为 TiKV 是一种 基于 Multi Raft 协议的分布式存储引擎 ，而不是像 Greenplum 或分库分表那种底层是多个 MySQL 或 PG 的单机数据库。

假如某集群要从 3 个 TiKV 节点扩容到 4 个 TiKV 节点，扩容步骤大致可以概括如下：

1.扩容 TiKV 节点 。集群增加一个 TiKV 4 节点，此时 TiKV 4 上没有任何 Region。PD 节点识别到新的 TiKV 节点启动负载调度机制，计算哪些 Region 需要迁移到 TiKV ４。

2.调度算法确定迁移 Region 。PD 节点根据调度机制，确定将哪些 Region 副本迁移到 TiKV 4 上（假如开始 3 个节点上各有 6 个 Region ，平均到 4 个节点后每个节点的 Region 数为 18/4=4~5 个副本）。PD 对 TiKV1~3 上 Region 对应的 Leader 副本发起复制指令。

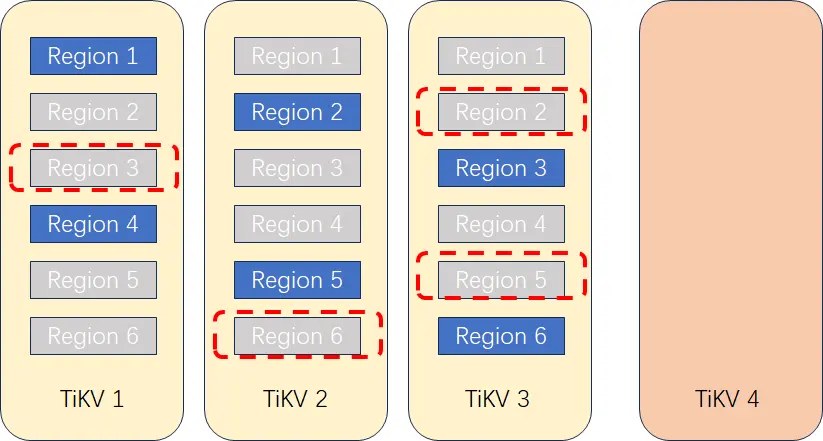
3.复制 Region 到新节点 。在 TiKV 上创建要复制的 Region 的副本，通过 Raft 机制开始复制数据。此过程中应用读写访问不受影响，不过因复制过程产生的 IO 消耗可能会对性能产生一点影响，不过 TiDB 本身提供了流控，可以动态调整复制的速度。

4.删除多余 Region 。Region 复制完成且数据一致后，PD 将发起删除原有副本指令，保证每个 Region 的副本只有 3 个。

5.Leader 重新均衡 。PD 根据调度机制，需要均衡 Leader 副本，将一部分 Region 的 Leader 切换到新增节点 TiKV 4 上，保证 Leader 的均衡。Leader 切换完成后，读写业务将自动路由到 TiKV 4 上实现业务负载均衡。

上述步骤简单理解下来就是说，TiKV 的扩容是一种 先生成副本再迁移 Leader 的一个过程，扩容对业务有影响的地方主要在于生成副本产生的 IO 消耗以及 Leader 切换的影响。对于前者，数据库有流控机制可以保证对业务几乎没有影响；对于后者，一方面 Leader 的切换本身时间非常短，另一方面当 TiDB 意识到 Region 迁移后也能够通过内部重试保证前端业务的正常执行。因此， 存储节点的扩容也几乎不会影响现有的业务。