Decoupled Knowledge Distillation解耦知识蒸馏
现有的蒸馏方法主要是基于从中间层提取深层特征,而忽略了Logit蒸馏的重要性。为了给logit蒸馏研究提供一个新的视角,我们将经典的KD损失重新表述为两部分,即目标类知识蒸馏(TCKD)和非目标类知识蒸馏(NCKD)。我们实证研究并证明了两部分的效果:TCKD转移了关于训练样本“难度”的知识,而NCKD是logit蒸馏有效的突出原因。更重要的是,我们揭示了经典KD损失是一个耦合公式,它(1)抑制了NCKD的有效性,(2)限制了平衡这两个部分的灵活性。为了解决这些问题,我们提出了解耦知识蒸馏(DKD),使TCKD和NCKD更有效和灵活地发挥其作用。
介绍
在过去的几十年里,计算机视觉领域已经被深度神经网络(DNN)彻底改变,它成功地促进了各种真实场景的任务,如图像分类、目标检测和语义分割。然而,大的网络通常受益于大的模型容量,引入了高计算和存储成本。在广泛部署轻量级模型的工业应用中,这样的成本并不可取。在文献中,降低成本的一个潜在方向是知识蒸馏(KD)。KD代表了一系列专注于将知识从重模型(教师)——转移到轻模型(学生)的方法,这可以在不引入额外成本的情况下提高轻模型的性能。
KD的概念在[12]中首次提出,通过最小化教师和学生预测logit之间的KL-Divergence来转移知识(图1a)。

自[28]以来,大部分的研究注意力都集中在从中间层的深层特征中提取知识。与基于logit的方法相比,特征蒸馏的性能在各种任务上是否表现出色,因此,对logit蒸馏的研究很少涉及。然而,基于特征方法的训练成本并不令人满意,因为在训练期间引入了额外的计算和存储使用(例如,网络模块和复杂的操作)来提取深度特征。
Logit蒸馏需要边际的计算和存储成本,但性能较差。直观的说,logit蒸馏应该达到与特征蒸馏相当的性能,因为logit比深度特征处于更高的语义层。假设logit蒸馏的潜力收到未知原因的限制,导致性能不理想。为了振兴基于Logit的方法,我们通过深入研究KD的机制开始这项工作。首先,我们将分类预测分为两个层次:(1)对目标类和所有非目标类进行二值预测;(2)对每个非目标类进行多类预测。在此基础上,我们将经典KD损失[12]重新表述为两部分,如图1b所示。一种是针对目标类的二元logit蒸馏,另一种是针对非目标类的多类别logit蒸馏。为了简化期间,我们将其分别命名为目标分类和知识蒸馏(TCKD)和非目标分类知识蒸馏(NCKD)。重新配方使我们能够独立地研究这两部分的效果。
TCKD通过二元logit蒸馏传递知识,这意味这只提供目标类的预测,而每个非目标类的具体预测是未知的。一个合理的假设是,TCKD传递了关于训练样本“难易度”的知识,即知识描述了识别每个训练样本的难易程度。为了验证这一点,我们从三个方面设计实验来提高训练数据的“难度”,即更强的增强、更嘈杂的标签和具有固有挑战性的数据集。
NCKD只考虑非目标logit之间的知识。有趣的是,我们通过经验证明,仅应用NCKD就可以获得与经典KD相当甚至更好的结果,这表明非目标logit中包含的知识至关重要,这可能是突出的“暗知识”。
更重要的是,我们的重新表述表明,经典KD损失是一个高度耦合的表述(如图1b所示),这可能是logit蒸馏潜力有限的原因。首先,NCKD损失项被一个与教师对目标类别的预测置信度负相关的系数加权。因此较大的预测分数将导致较小的权重。这种耦合显著抑制了NCKD对良好预测训练样本的影响。这种抑制并不可取,因为教师对训练样本越有信息,可提供的知识越可靠越有价值。其次,TCKD和NCKD的意义是耦合的,即不允许分别对TCKD和NCKD进行加权。这种限制是不可取的,因为TCKD和NCKD应该分开考虑,因为它们的贡献来自不同的方面。
为了解决这些问题,我们提出了一种灵活高效的logit蒸馏方法,称为解耦知识蒸馏(DKD,图1b)。DKD将NCKD损失从与教师置信度负相关的系数中解耦,将其替换为恒定值,从而提高了对预测良好的样本的蒸馏效率。同时,对NCKD和TCKD也进行了解耦,通过调整各部分权重,可以分别考虑NCKD和TCKD的重要性。
总的来说,我们的贡献总结如下:
(1)将经典的logit蒸馏分为TCKD和NCKD,为Logit蒸馏的研究提供了新的思路。
(2)我们揭示了由其高耦合公式引起的经典KD损失的局限性。NCKD与教师信心的耦合抑制了知识转移的有效性。TCKD与NCKD的耦合限制了平衡两部分的灵活性。
(3)为了克服这些局限性,我们提供了一种有效的logit蒸馏方法DKD。
重新思考知识蒸馏
在本节中,我们深入探讨知识蒸馏的机制。我们将KD损失重新表述为两部分的加权和,一部分与目标类相关,另一部分与目标类无关。我们探讨了知识蒸馏框架中每个部分的作用,并揭示了经典KD的一些局限性。受此启发,我们进一步提出了一种新的logit蒸馏方法,在各种任务上取得了显著的性能。
回顾KD
Notation对于第t类的训练样本,分类概率可以表示为P=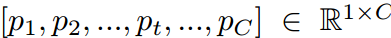 ,其中pi是第i类的概率,C是类的个数。p中的每个元素都可以通过softmax函数得到:
,其中pi是第i类的概率,C是类的个数。p中的每个元素都可以通过softmax函数得到:
p
i
=
e
x
p
(
z
i
)
∑
j
=
1
C
e
x
p
(
z
j
)
p_i = \frac{exp(z_i)}{\sum_{j=1}^Cexp(z_j)}
pi=∑j=1Cexp(zj)exp(zi)
其中zi代表第i类的对数。
为了区分于目标类相关和不相关的预测,我们定义了以下符号。b = 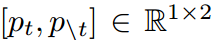 表示目标类(pt)和其他所有非目标类(p\t)的二值概率,其计算公式为:
表示目标类(pt)和其他所有非目标类(p\t)的二值概率,其计算公式为:
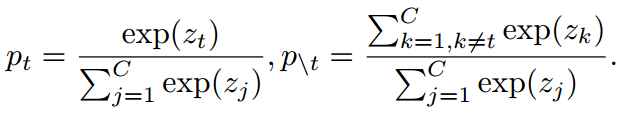
同时,我们声明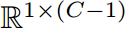 独立建模非目标类之间的概率(即,不考虑第t类)。每个元素的计算方法为:
独立建模非目标类之间的概率(即,不考虑第t类)。每个元素的计算方法为: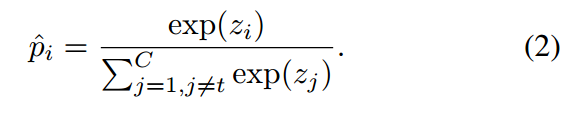
Reformulation 在第一部分中,我们尝试用二元概率b和非目标类之间的概率p来重新表述KD。T和S分别表示老师和学生。经典KD使用kl散度作为损失函数,也可以写成2:
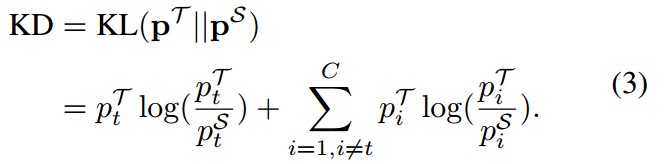
根据等式(1)和等式(2)我们有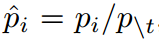 ,所以我们可以把等式(3)改写为:
,所以我们可以把等式(3)改写为:
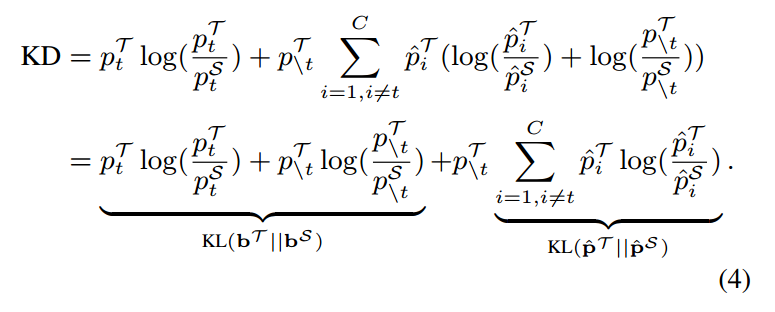
等式(4)可以改写为:

如公式(5)所示,KD损失被重新表述为两项的加权和。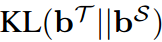 表示目标类别的教师和学生的二元概率之间的相似度。因此,我们将其命名为目标类知识蒸馏(TCKD)。同时,
表示目标类别的教师和学生的二元概率之间的相似度。因此,我们将其命名为目标类知识蒸馏(TCKD)。同时, 表示非目标类中教师和学生概率的相似度,称为非目标类知识蒸馏(NVKD)。式(5)可以改写为:
表示非目标类中教师和学生概率的相似度,称为非目标类知识蒸馏(NVKD)。式(5)可以改写为:
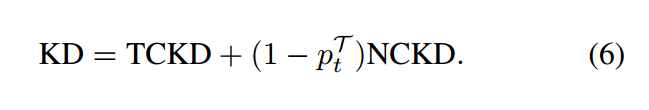
显然,NCKD的重建与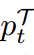 是耦合的。
是耦合的。
上述重新表述启发了我们对TCKD和NCKD的个体效应进行研究,这将揭示经典耦合表述的局限性。
TCKD和NCKD的影响
各部件的性能增益。我们分别研究了TCKD和NCKD对CIFAR-100的影响。选择ResNet、WideResNet(WRN)和ShuffleNet作为训练模型,其中考虑了相同和不同的架构。实验结果如表1,对于每个师生对,我们报告了(1)学生基线,(2)经典KD(其中同时使用TCKD和NCKD),(3)单一TCKD和(4)单一NCKD的结果。每个损失的权重设置为1.0(包括默认的交叉熵损失)。其它实现细节与第4节相同。

直观地说,TCKD集中于与目标类相关的知识,因为相应的损失函数只考虑二进制概率。相反,NCKD侧重于非目标类别的知识。我们注意到单独使用TCKD对学生来说可能没有帮助(例如在ShufflerNet-V1上增加0.02%和0.12%)甚至是有害的(例如,在WRN-16-2上下降2.3%,在ResNet8-4上下降3.87%)。然而,NCKD的蒸馏性能与经典KD相当,甚至更好(例如,在ResNet8/4上,1.76% vs 1.13%)。消融结果表明靶类相关知识不如非靶类知识重要,为了深度研究这一现象,我们提供如下进一步的分析。
TCKD传递了关于训练样本“难度”的知识
根据等式(5),TCKD通过二值分类任务传递“暗知识”,这可能与样本的“难度“有关。例如,与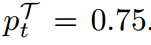 的训练样本相比,
的训练样本相比, 的训练样本可能”更容易“让学生学习。由于TCKD传达了训练样本的“难度”,我们假设当训练数据变得具有挑战性时,有效性将被解释。然而,CIFRA-100训练集很容易过拟合。因此,教师提供的“难度”知识并不是信息性的。在这一部分中,我们从三个角度进行实验验证:训练数据越难,TCKD提供的好处越多。
的训练样本可能”更容易“让学生学习。由于TCKD传达了训练样本的“难度”,我们假设当训练数据变得具有挑战性时,有效性将被解释。然而,CIFRA-100训练集很容易过拟合。因此,教师提供的“难度”知识并不是信息性的。在这一部分中,我们从三个角度进行实验验证:训练数据越难,TCKD提供的好处越多。
(1)应用强增强是增加训练数据难度的一种直接方法。我们在CIFAR-100上使用AutoAugment训练ResNet32×4模型作为教师,获得了81.29%的top-1验证精度。对于学生,我们训练带/不带TCKD的ResNet8、4和ShufflerNetv1模型。表2的结果表明,如果应用强增强,TCKD可以获得显著的性能增益。

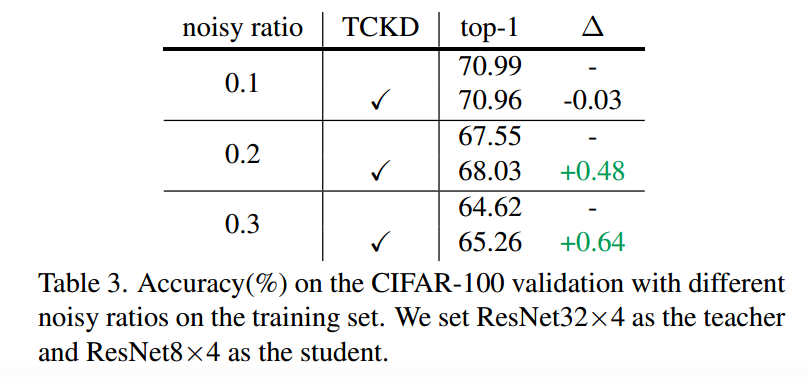
(2)噪声标签也会增加训练数据的难度。我们在CIFAR-100上以{0.1,0.2,0.3}对称噪声比训练ResNet32×4模型作为教师,ResNet8×4模型作为学生,如下[7,35]。如表3所示,结果表明TCKD在噪声较大的训练数据上取得了更多的绩效提升。
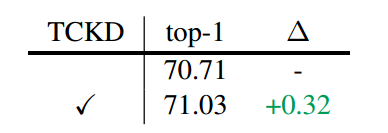
(3)挑战性的数据集(例如,ImageNet也被考虑。表4显示,TCKD可以在ImageNet上带来+0.32%的性能增益。
最后,我们通过实验各种策略来增加训练数据的难度(如强增强、噪声标签、困难任务),证明了TCKD的有效性。结果证明,在提取更具挑战性的训练数据时,有关训练样本“难度“的知识可能更有用。
NCKD是logit蒸馏工作的重要原因,但受到很大的抑制。有趣的是,我们在表1中注意到,当仅应用NCKD时,性能与经典KD相当甚至更好。结果表明,非目标类的知识对logit蒸馏至关重要,可以成为突出的“暗知识”。然而,通过回顾方程(5),我们注意到NCKD损失与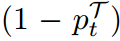 相耦合。其中,
相耦合。其中,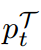 代表教师对目标类别的置信度。因此,更有置信度的预测会导致更小的NCKD权重。我们假设教师对训练样本越有信心,它提供的知识就越可靠,越有价值。然而,这种自信的预测高度抑制了损失权重。我们假设这一事实会限制知识蒸馏的有效性,这首先是由于我们在等式(5)中对KD的重新表述而研究的。
代表教师对目标类别的置信度。因此,更有置信度的预测会导致更小的NCKD权重。我们假设教师对训练样本越有信心,它提供的知识就越可靠,越有价值。然而,这种自信的预测高度抑制了损失权重。我们假设这一事实会限制知识蒸馏的有效性,这首先是由于我们在等式(5)中对KD的重新表述而研究的。
我们设计了一个消融实验来验证预测良好的样本确实比其他样本更好地传递知识。首先,我们根据 对训练样本进行排序,并将其平均分成两个子集。为了清晰起见,一个子集包括
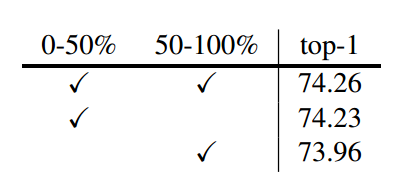
对训练样本进行排序,并将其平均分成两个子集。为了清晰起见,一个子集包括 前50%的样本,而其余样本在另一个子集中。然后,我们在每个子集上使用NCKD训练学生网络,以比较性能增益(而交叉熵损失仍然在整个集合上)。表5显示,在前50%的样本上使用NCKD可以获得更好的性能,这表明预测良好的样本的知识比其他样本更丰富。然而,预测良好的样本的损失权重被教师的高置信度所抑制。
前50%的样本,而其余样本在另一个子集中。然后,我们在每个子集上使用NCKD训练学生网络,以比较性能增益(而交叉熵损失仍然在整个集合上)。表5显示,在前50%的样本上使用NCKD可以获得更好的性能,这表明预测良好的样本的知识比其他样本更丰富。然而,预测良好的样本的损失权重被教师的高置信度所抑制。
解耦知识蒸馏
至此,我们将经典KD损失重新表述为两个独立部分的加权和,进一步验证了TCKD的有效性,揭示了NCKD的抑制作用。具体来说,TCKD传递了关于训练样本“难度”的知识。TCKD可以在更具挑战性的训练数据上获得更显著的改进。NCKD在非目标类之间进行知识转移。当权重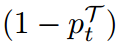 较小时,知识转移受到抑制。
较小时,知识转移受到抑制。
本能地,TCKD和NCKD都是必不可少的,至关重要的。然而,在经典KD公式中,TCKD和NCKD从以下几个方面耦合。
(1)首先,NCKD与 耦合,这可以抑制预测良好的样本上的NCKD。由于表5的结果表明,预测良好的样本可以带来更多的性能增益,因此耦合形式可能会限制NCKD的有效性。
耦合,这可以抑制预测良好的样本上的NCKD。由于表5的结果表明,预测良好的样本可以带来更多的性能增益,因此耦合形式可能会限制NCKD的有效性。
(2)另一方面,在经典KD框架下,NCKD与TCKD的权重是耦合的。不允许为了平衡重要性而改变每个词的权重。我们认为TCKD和NCKD应该考虑他们的贡献来自不同的方面而分离。
基于我们对KD的重新表述,我们提出了一种新的logit蒸馏方法——解耦知识蒸馏(DKD)。我们提出的DKD在解耦公式中独立考虑了TCKD和NCKD。具体来说,我们分别引入了两个超参数作为TCKD和NCKD的权重,DKD的损失函数为:

在DKD中,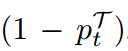 会抑制NCKD的有效性,使用
会抑制NCKD的有效性,使用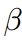 代替。此外,还允许调整两个超参数以平衡TCKD和NCKD的重要性。DKD通过解耦NCKD和TCKD,为logit蒸馏提供了高效、灵活的方法。算法1提供了DKD的伪代码。
代替。此外,还允许调整两个超参数以平衡TCKD和NCKD的重要性。DKD通过解耦NCKD和TCKD,为logit蒸馏提供了高效、灵活的方法。算法1提供了DKD的伪代码。