一、哈希表是什么?
哈希表,也称为散列表,是一种根据关键码值(Key value)直接进行访问的数据结构。它通过把关键码值映射到表中一个位置来访问记录,从而加快查找速度。这个映射函数叫做散列函数(哈希函数),而存放记录的数组则称为散列表。
二、哈希表的构成(开放地址法)
我们先了解一下哈希表是如何构成的?
实现一个基本的哈希表数据结构涉及到几个核心步骤:
1、创建哈希表本身的数据结构,
2、定义一个哈希函数,
3、处理哈希冲突(本文以开放地址法为例)
开放地址法(Open Addressing)是哈希表解决哈希冲突的一种策略。当发生哈希冲突时,即两个或更多的键具有相同的哈希值,开放地址法通过在数组中查找下一个可用的空位来解决冲突。这种方法的核心思想是不再依赖哈希函数给出的数组下标,而是顺序查看表中的下一个单元,直到找到一个空单元或查遍全表。
开放地址法通常有以下三种具体实现方式:
线性探测:这是最简单的一种开放地址法。当发生冲突时,顺序查看表中下一个单元,直到找到一个空单元或查遍全表。这种方法的核心思想是“一旦发生冲突,就去寻找下一个空的散列表地址”。
二次探测:这是另一种开放地址法,它在发生冲突时,不是简单地顺序查看下一个单元,而是根据某种二次方程来确定下一个要查看的单元位置。
双重散列:这种方法使用两个哈希函数。当第一个哈希函数发生冲突时,使用第二个哈希函数来确定下一个要查看的单元位置。
这里我们用C语言更加方便举例,后面附带代码图解。
首先是创建哈希表本身的数据结构
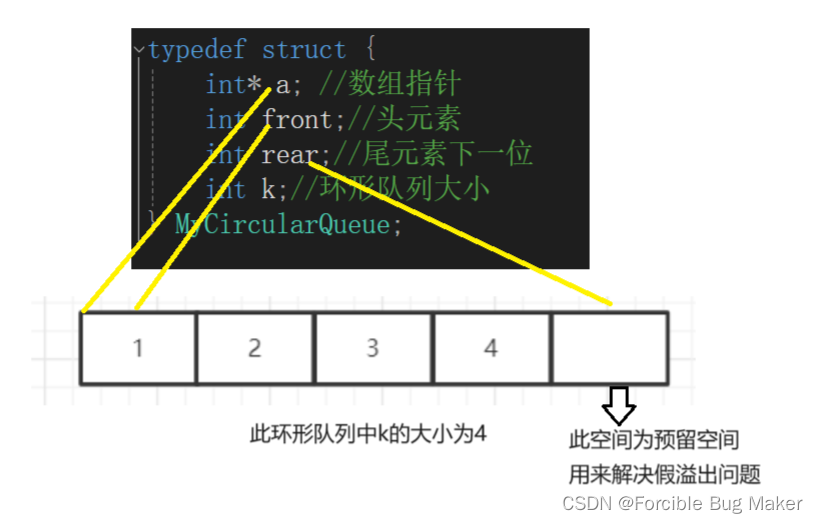
#define TABLE_SIZE 10
//先定义一个有key和value两种属性的结构体
//该结构体的名字是KeyValuePair
typedef struct {
int key;
int value;
} KeyValuePair;
// 哈希表结构
//定义一个结构体,里面有KeyValuePair结构体的数组
//该结构体的名字是HashTable
typedef struct {
KeyValuePair pairs[TABLE_SIZE];
//暂时定为哈希表的容量为10
//数组名为pairs
} HashTable;
定义一个哈希函数
// 简单的哈希函数
unsigned int hash(int key) {
//将key值求余以表的容量10
return key % TABLE_SIZE;
}
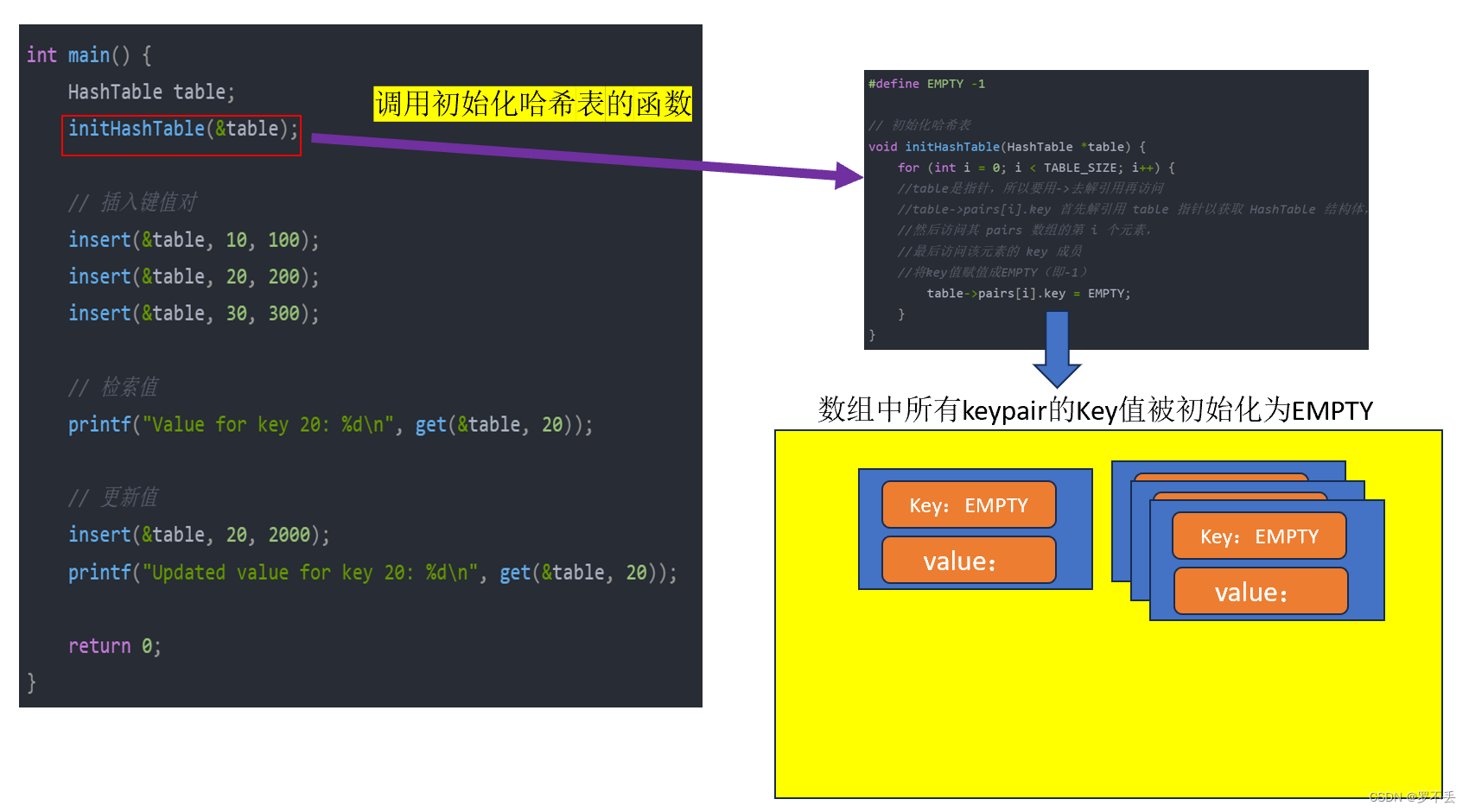
定义一个初始化哈希表的函数
#define EMPTY -1
// 初始化哈希表
void initHashTable(HashTable *table) {
for (int i = 0; i < TABLE_SIZE; i++) {
//table是指针,所以要用->去解引用再访问
//table->pairs[i].key 首先解引用 table 指针以获取 HashTable 结构体,
//然后访问其 pairs 数组的第 i 个元素,
//最后访问该元素的 key 成员
//将key值赋值成EMPTY(即-1)
table->pairs[i].key = EMPTY;
}
}
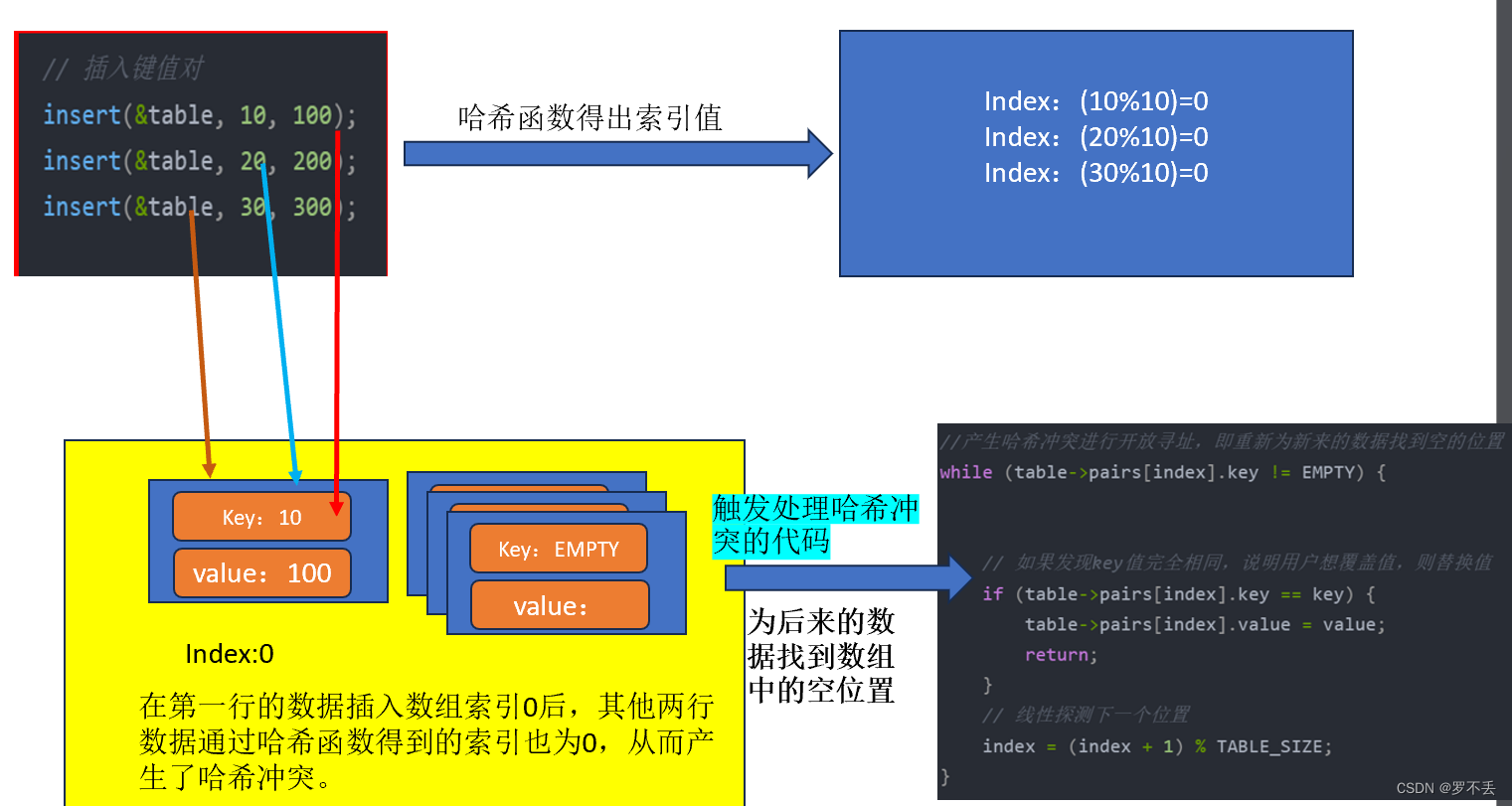
创建一个插入值到哈希表的函数,里面需要进行哈希冲突的处理
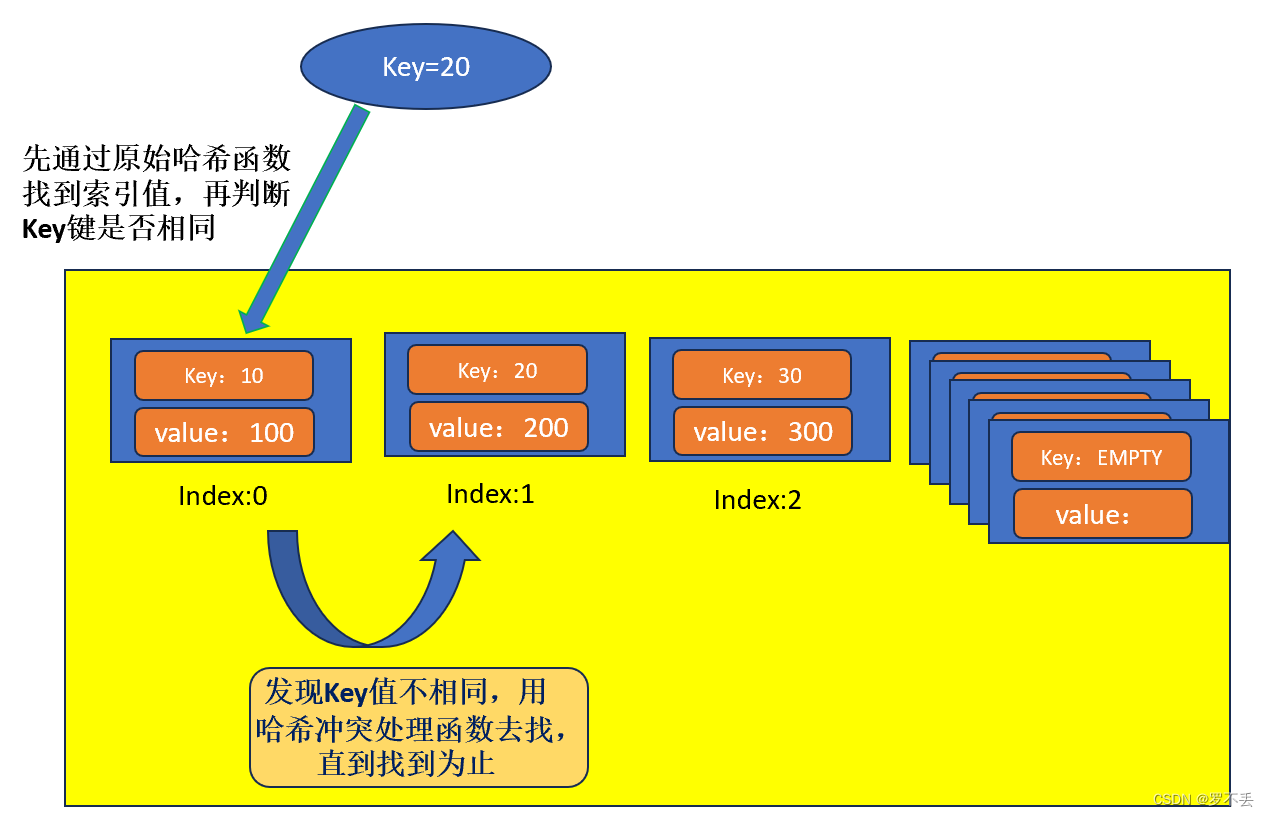
哈希冲突:将数据插入表中时,数据通过哈希函数计算出来的索引值来找到自己的位置,而数组索引处已有数据,产生冲突。
通俗点,两个数据想要插在数组的同一位置,必须要做一定处理
// 向哈希表中插入键值对
void insert(HashTable *table, int key, int value) {
unsigned int index = hash(key);
//通过哈希函数对Key值的运算得到索引index的值
//产生哈希冲突进行开放寻址,即重新为新来的数据找到空的位置
while (table->pairs[index].key != EMPTY) {
// 如果发现key值完全相同,说明用户想覆盖值,则替换值
if (table->pairs[index].key == key) {
table->pairs[index].value = value;
return;
}
// 线性探测下一个位置
index = (index + 1) % TABLE_SIZE;
}
// 找到空位置并插入
table->pairs[index].key = key;
table->pairs[index].value = value;
}
创建一个查询哈希表数据的函数
// 从哈希表中检索值
int get(HashTable *table, int key) {
unsigned int index = hash(key);
while (table->pairs[index].key != EMPTY) {
// 找到键,返回对应的值
if (table->pairs[index].key == key) {
return table->pairs[index].value;
}
// 线性探测下一个位置
index = (index + 1) % TABLE_SIZE;
}
// 没找到键,返回错误值
return -1;
}
测试主函数
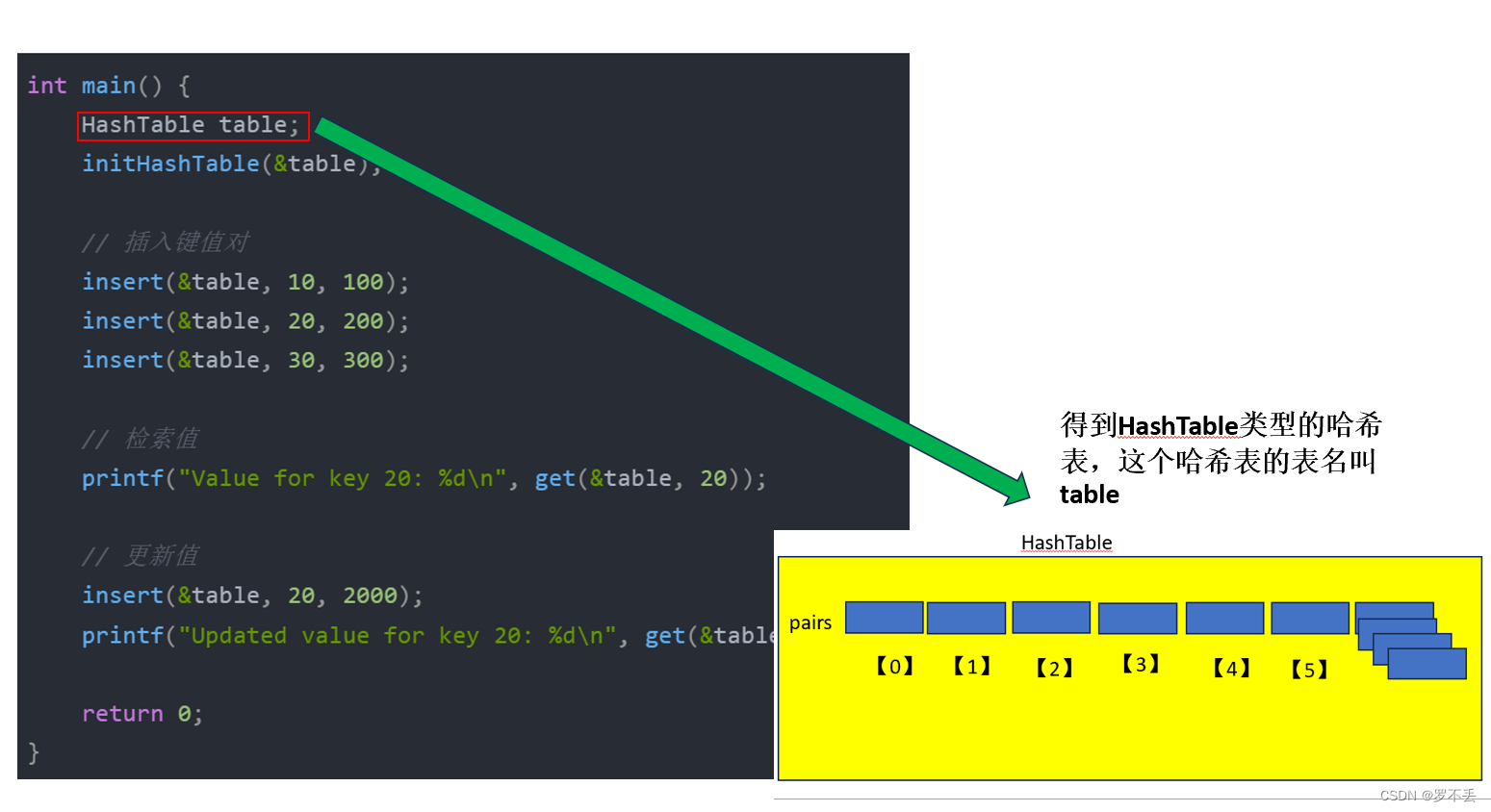
int main() {
HashTable table;
initHashTable(&table);
// 插入键值对
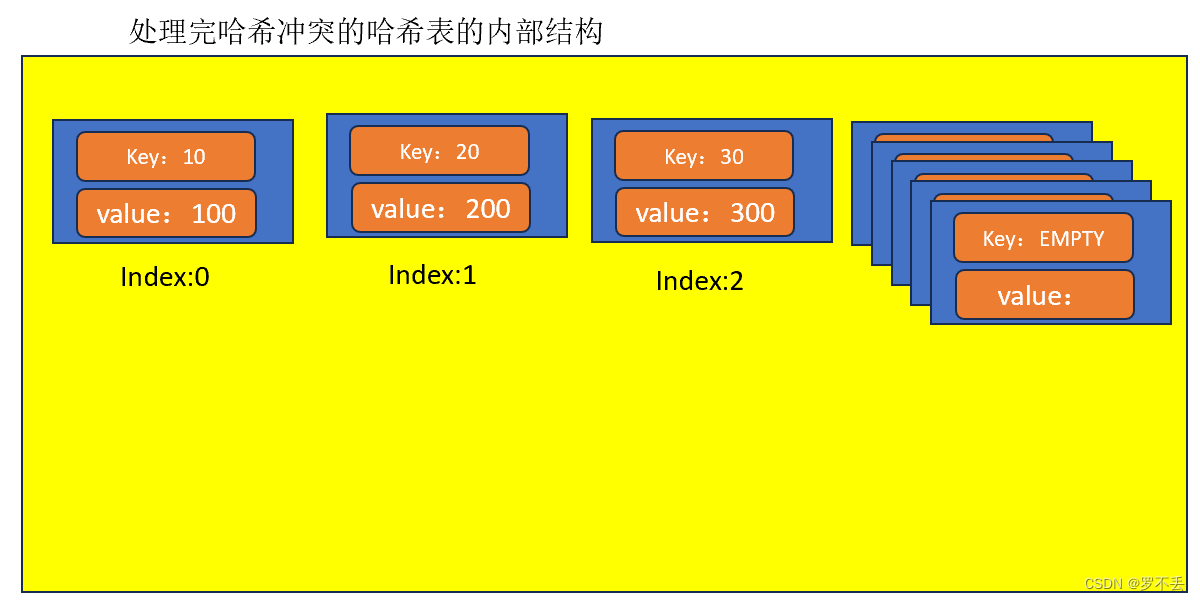
insert(&table, 10, 100);
insert(&table, 20, 200);
insert(&table, 30, 300);
// 检索值
printf("Value for key 20: %d\n", get(&table, 20));
// 更新值
insert(&table, 20, 2000);
printf("Updated value for key 20: %d\n", get(&table, 20));
return 0;
}
例子代码图解
图【1】
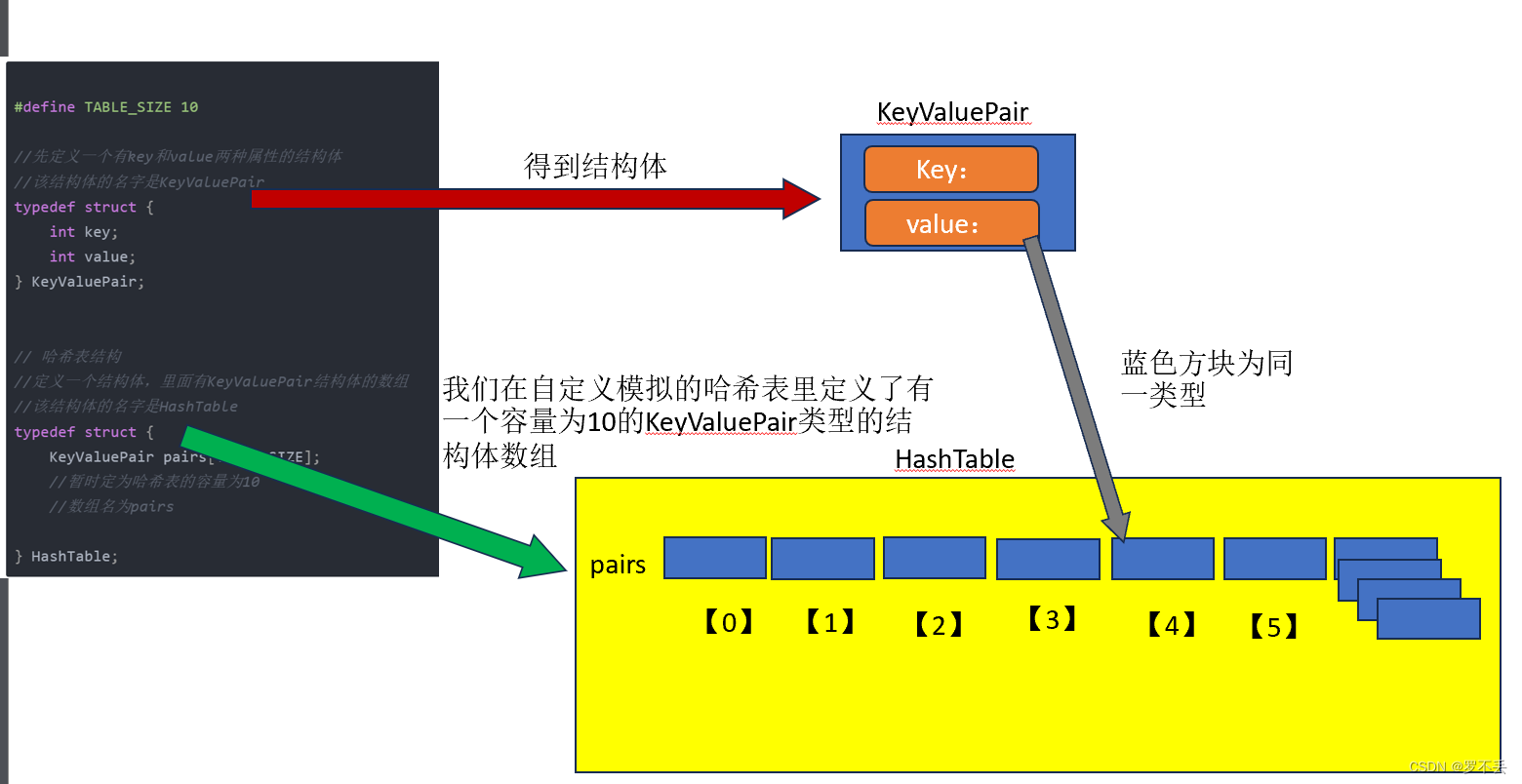
图【2】
图【3】
图【4】

图【5】
图【6】
图【7】
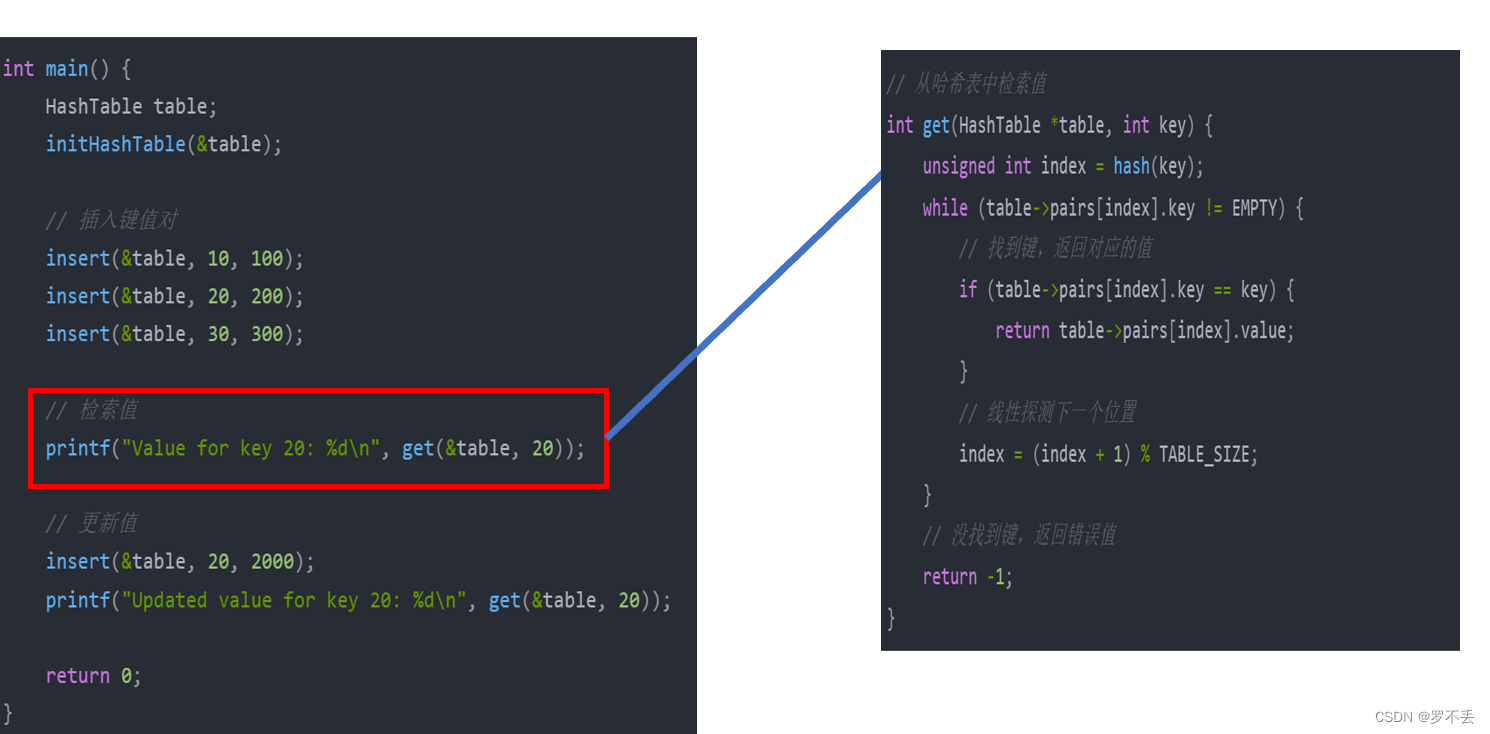
图【8】
三、哈希表的构成(链地址法)
处理哈希冲突时,主要有开放地址法和链地址法这两种方法,上面的代码和图解已经介绍了开放地址法
而链地址法也是一种优雅的冲突解决策略。
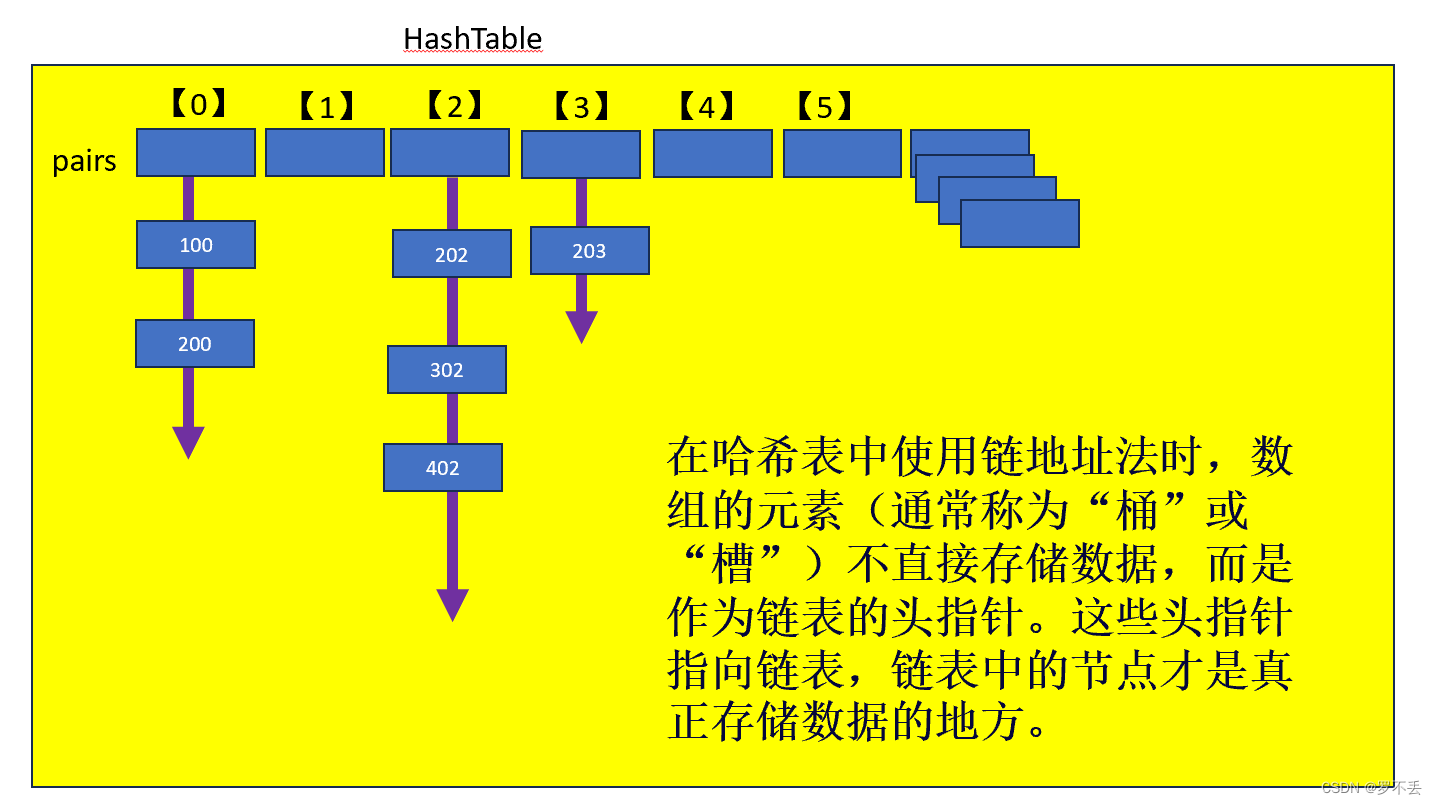
实现步骤:
初始化:
创建一个数组,每个元素都是一个链表的头指针。
哈希函数:选择一个合适的哈希函数,将键映射到数组的某个索引。
插入:
计算键的哈希值,找到对应的数组索引。
如果该索引的链表为空,直接插入数据。
如果链表不为空,遍历链表查找:
若找到相同键,更新值。
若未找到,在链表末尾插入新数据。
查找:
计算键的哈希值,找到对应的链表。
遍历链表,比较键,直到找到或遍历完。
删除:
计算键的哈希值,找到对应的链表。
遍历链表,找到要删除的数据并移除。
链地址法通过链表巧妙地解决了哈希冲突,使得哈希表在冲突较多的情况下仍能保持高效。
四、开放地址法与链地址方法时间复杂度比较
开放地址法
开放地址法的时间复杂度分析相对复杂,因为它依赖于哈希表的装载因子(即已存储元素数量与哈希表大小的比值)以及哈希函数的均匀分布性。
插入操作
平均情况:当哈希表的大小足够大且装载因子较低时,插入操作的平均时间复杂度接近O(1),因为空闲位置较多,冲突较少。
最坏情况:当哈希表的大小较小或装载因子接近1时,插入操作的时间复杂度可能退化为O(n),其中n是哈希表中的元素数量。这是因为连续的冲突可能导致需要遍历整个哈希表来找到空闲位置。
查找操作
平均情况:与插入操作类似,当哈希表的大小足够大且装载因子较低时,查找操作的平均时间复杂度接近O(1)。
最坏情况:当哈希表的大小较小或装载因子接近1时,查找操作的时间复杂度可能退化为O(n),特别是当发生堆积(即大量元素集中在哈希表的某些区域)时。
链地址法
链地址法的时间复杂度分析相对简单,因为它不依赖于哈希表的装载因子。
插入操作
平均情况:无论哈希表的大小和装载因子如何,插入操作的平均时间复杂度都是O(1),因为插入总是在链表的末尾进行。
最坏情况:最坏情况下,当所有的元素都哈希到同一个桶(即链表)时,插入操作的时间复杂度为O(n),其中n是链表的长度。然而,这种情况在良好的哈希函数和适当的哈希表大小下是很少见的。
查找操作
平均情况:查找操作的平均时间复杂度是O(1 + α),其中α是链表的平均长度。这是因为查找操作通常只需要遍历链表一次。
最坏情况:最坏情况下,当所有的元素都哈希到同一个桶时,查找操作的时间复杂度为O(n),其中n是链表的长度。
开放地址法和链地址法在平均情况下的时间复杂度都是O(1),但在最坏情况下,开放地址法的时间复杂度可能更高,因为它可能需要进行多次探测来找到空闲位置或查找元素。而链地址法则在最坏情况下可能面临链表过长的问题,但在良好的哈希函数和适当的哈希表大小下,这种情况是不常见的。因此,选择哪种方法取决于具体的应用场景和需求。
五、哈希表的应用场景
哈希表因其高效的查找和插入性能,被广泛应用于各种场景。以下是哈希表的一些典型应用:
数据库索引
数据库索引是哈希表的一个重要应用。通过索引,可以快速定位到数据库中的特定数据,提高查询效率。
缓存系统
缓存系统通常使用哈希表来存储热点数据,以便快速响应请求。当数据被访问时,将其存储在哈希表中,以便后续快速查找。
唯一性检查
哈希表可以用于检查数据的唯一性。通过计算数据的哈希值,可以快速判断数据是否已经存在于哈希表中。