Mixtral模型解读

news2024/11/16 1:48:06

Mixtral 8x7B(Mistral MoE)

1.Mistral 7B模型

Mistral 7B模型与Llama2 7B模型结构整体上是相似的，其结构参数如下所示。

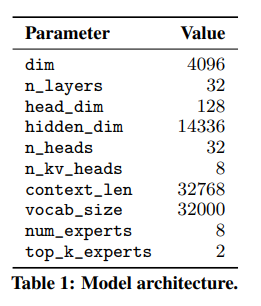
细节上来说，他有两点不同。

1.1SWA(Sliding Window Attention)

一般的Attention来说，是Q与KV-Cache做内积，然后求出新的KV。其中KV.shape = [batch_size, num_heads, seq_len, dim]。Llama2中的GQA是在多头上做文章，即让多组Q共享一组KV。而SWA是在seq_len上做文章，即限定attention的视野范围在Window中。

这是原本一个7x7的mask矩阵

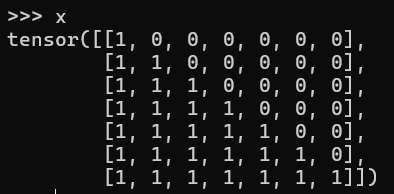
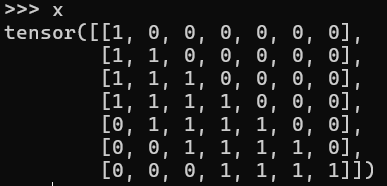
而这时Slide Window=3的mask矩阵

if input_ids.shape[1] > 1:
    # seqlen推理时在prompt阶段为n，在generation阶段为1
    seqlen = input_ids.shape[1]
    # mask在推理时也只在prompt阶段有,
    #定义一个全1方阵
    tensor = torch.full((seqlen, seqlen),fill_value=1)
    # 上三角部分全为0
    mask = torch.tril(tensor, diagonal=0).to(h.dtype)
    # 这里代码diagonal应该等于(-self.args.sliding_window+1)才能满足window size为 sliding_window
    mask = torch.triu(mask, diagonal=-self.args.sliding_window)
    mask = torch.log(mask)

而在generation阶段，因为是自回归生成所以mask起不到作用。此时mistral则使用了RotatingBufferCache来实现此操作。

# The cache is a rotating buffer
# positions[-self.sliding_window:] 取最后w个位置的索引，取余
# [None, :, None, None]操作用于扩维度[1,w,1,1]
scatter_pos = (positions[-self.sliding_window:] % self.sliding_window)[None, :, None, None]
# repeat操作repeat维度 [bsz, w, kv_head, head_dim]
scatter_pos = scatter_pos.repeat(bsz, 1, self.n_kv_heads, self.args.head_dim)
# src取[:,-w,:,:] 所以src.shape=[bsz,w,kv_head,head_dim]
# 根据scatter_pos作为index 将src写入cache
self.cache_k[:bsz].scatter_(dim=1, index=scatter_pos, src=xk[:, -self.sliding_window:])
self.cache_v[:bsz].scatter_(dim=1, index=scatter_pos, src=xv[:, -self.sliding_window:])

自然，我们会有疑问。只让Q与前面Window Size的KV计算Attention，不会影响最终的预测精度吗？

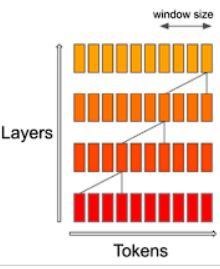
官方给出了这张图片。具体来说窗口确实限制了attention的视野范围。但是并不是完全无法观察到窗口外的信息。

例子：

第1层：
- "A"只能看到自己。
- “B"看到"A"和"B”。
- “C"看到"B"和"C”。
- “D"看到"C"和"D”。
- “E"看到"D"和"E”。
在第1层结束时，“E"直接关注了"D”，间接接收了"C"的影响。
第2层：
- "A"依然只能看到自己。
- “B"现在可以看到经过第1层处理的"A"和"B”。
- “C"可以看到经过第1层处理的"B"和"C”，这意味着"C"现在间接包含了"A"的信息。
- “D"可以看到经过第1层处理的"C"和"D”，间接包含了"B"的信息。
- “E"可以看到经过第1层处理的"D"和"E”，间接包含了"C"的信息，而"C"又包含了"A"的信息。
在第2层结束时，“E"直接关注了"D”（包含"C"的信息），间接关注了"C"（包含"A"和"B"的信息）。

综上所述，对于 $layer_t$ 而言虽然 $Q_H$ 只能直接与 $tokens - {F,G,H}$ 直接进行注意力机制计算，但是却可以间接与更早的 $tokens - {G,F,E,D...}$ 参与注意力机制运算，以此类推，只要层数足够大，配合这种传递方式就可以覆盖整个序列。论文中还举例说明，对于一个序列长度是16k，Window Size为4K的SWA，只需要四层，最后一个token就能看到之前的全部token信息。

1.2MoE

MoE简单来说就是让一个网络模型有多条分支，每条分支代表一个Expert(专家)，每个Expert有擅长的领域，当面对不同的具体任务，可以通过一个门控单元来选择哪或哪几个Expert进行计算。当然在训练MoE模型时也要注意各个Experts负载均衡，防止赢者通吃，达不到想要的目的。
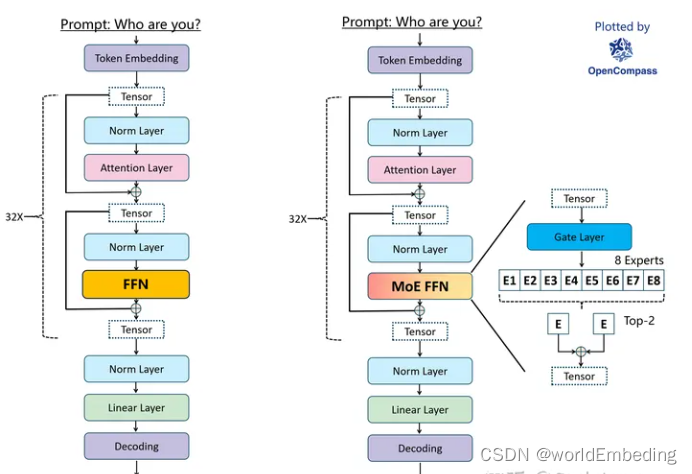
在这里插入图片描述
左边是Llama结构，右边是Mixtral。

"""
			代码中 epxerts 是 self.feed_forward = MoeLayer(
                experts=[FeedForward(args=args) for _ in range(args.moe.num_experts)],
                gate=nn.Linear(args.dim, args.moe.num_experts, bias=False),
                moe_args=args.moe)
                
                gate 是 linear(dim, num_experts)
""" 
class MoeLayer(nn.Module):
    def __init__(self, experts: List[nn.Module], gate: nn.Module, moe_args: MoeArgs):
        super().__init__()
        assert len(experts) > 0
        self.experts = nn.ModuleList(experts)
        self.gate = gate
        self.args = moe_args
        
    def forward(self, inputs: torch.Tensor):
        # inputs.shape = [B*L, D]
        gate_logits = self.gate(inputs)
        # 从 gate_logits 中选出, 得分最高的 topk 个专家
        weights, selected_experts = torch.topk(gate_logits, self.args.num_experts_per_tok)
        # 确保每个输入分配给专家的权重和为1，并将结果转换回输入的数据类型
        weights = F.softmax(weights, dim=1, dtype=torch.float).to(inputs.dtype)
        """
        	假设 softmax 后 weights 为 [0.2, 0.1, 0.7]， selected_experts 为 [1,3,4] 表明
        	模型认为第一个，第三个，第四个专家的意见占比分别 .2, .1, .7
        """
        results = torch.zeros_like(inputs)
        for i, expert in enumerate(self.experts):
            # torch.where : 给出 i 在 selected_experts 中的行和列
            batch_idx, nth_expert = torch.where(selected_experts == i)
            # 加权和，将输入放入专家网络 与 权值加权求和
            results[batch_idx] += weights[batch_idx, nth_expert, None] * expert(inputs[batch_idx])
        return results