语言模型:NLP经典的模型

1.语言模型
①长度为T的文本序列中词元依次是x1,…,xT,xT被认为是文本序列在时间t处的观测或标签。在给定文本序列,语言模型的目标是估计序列的联合概率p(x1,…,xT)
②序列模型的核心是整个序列文本所出现的概率
应用:
①做预训练模型(BERT,GPT-3):给定大量的文本做预训练,然后训练模型预测整个文本出现的概率,能够得到较多的训练数据来做较大的模型
②生成文本,给定前面几个词,预测后续的文本。但是对模型要求比较高,否则产生误差不断积累。
③判断哪个序列比较常见,使用常见的语言模型判断哪一个序列出现的概率高
2.使用计数来建模——语言模型可以使用计数进行建模
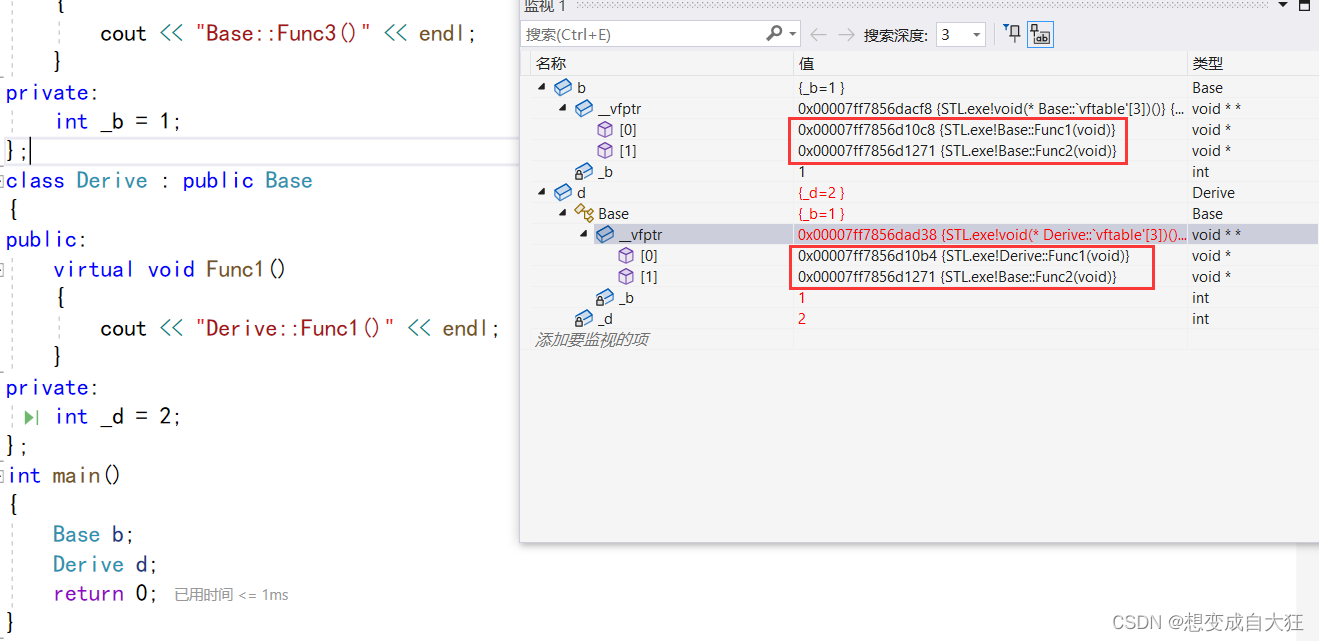
①假设序列长度为2

n:总词数,采集的所有样本,n(x)单个x单词出现的次数,n(x,x`)是连续单词对出现的次数
②序列长度为3
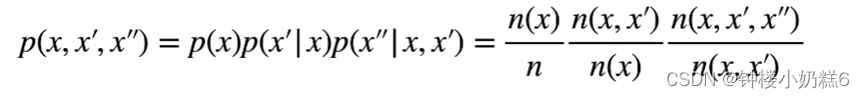
3.N元语法
①当序列很长时,因为文本量不够大,很可能n(x1,…,xT)<=1
②使用马尔可夫假设解决这个问题
Ⅰ一元语法

tau=0,计算xt的概率时,不用考虑xt之前的数据,认为每个词是独立的。
Ⅱ二元语法

tau=1,每次计算xt的概率时,只依赖于x(t-1),每个词和前面一个词是相关的
Ⅲ三元语法

tau=2, 每次计算xt的概率时,只依赖于x(t-1)和x(t-2),每个词和前面两个词是相关的
③对于N元语法来说,子序列的长度是固定的。N越大,对应的以来关系越长,精度高,但是时间复杂度大
④二元语法,三元语法比较常见
4.N元语法的优点:
①最大的优点是处理比较长的序列。序列很长复杂度是指数级别的
②任意长度的序列,N元语法扫描的子序列长度是固定的。对于二元语法说,每次看长为2的子序列首先将长度为 2 的组成任何一个词 n(x1,x2)的总数存下来,n(x1)出现的概率存起来,把n存起来。
③马尔可夫假设的N元语法的好处是,将词存起来。计算的复杂度O(T)而不是O(N)。查询一个任意长度的序列的时间复杂度为 o(T),T 是序列长度。N越大精度越高。随着N增大,空间复杂度增大。二元,三元语法比较常见。
【总结】
①语言模型估计文本序列的联合概率
②使用统计方法时采用n元语法