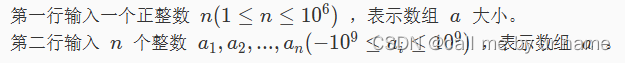递推

斐波那契(Fibonacii)数列的递推公式：F(n) = F(n -1) + F(n - 2)

错排问题：F(n) = (n-1) * [F(n-1)+F(n-2)]
解释

例题

一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 10 级的台阶总共有多少种跳法

思路

要想跳到第10级台阶，要么是先跳到第9级，然后再跳1级台阶上去;要么是先跳到第8级，然后一次迈2级台阶上去。
同理，要想跳到第9级台阶，要么是先跳到第8级，然后再跳1级台阶上去;要么是先跳到第7级，然后一次迈2级台阶上去。
要想跳到第8级台阶，要么是先跳到第7级，然后再跳1级台阶上去;要么是先跳到第6级，然后一次迈2级台阶上去。

f（10） = f（9）+f(8)
f (9) = f(8) + f(7)
f (8) = f(7) + f(6)
…
f(3) = f(2) + f(1)

即通用公式为: f(n) = f(n-1) + f(n-2)

动态规划

根据一类多阶段问题的特点，把多阶段决策问题变换为一系列互相联系的单阶段问题，然后逐个加以解决
最优化原理，动态规划算法通常用于求解具有某种最优性质的问题。*在这类问题中，可能会有许多可行解。每一个解都对应与一个值，找到具有最优值的解
用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到，只要它被计算过，就将其结果填入表中。这就是动态规划的基本思路。

基本思路

穷举分析：当台阶数是1的时候，有一种跳法，f（1） =1；当只有2级台阶时，有两种跳法，第一种是直接跳两级，第二种是先跳一级，然后再跳一级。即f(2) = 2；当台阶是3级时，想跳到第3级台阶，要么是先跳到第2级，然后再跳1级台阶上去，要么是先跳到第 1级，然后一次迈 2 级台阶上去。所以f(3) = f(2) + f(1) =3；当台阶是4级时，想跳到第3级台阶，要么是先跳到第3级，然后再跳1级台阶上去，要么是先跳到第 2级，然后一次迈 2 级台阶上去。所以f(4) = f(3) + f(2) =5；当台阶是5级时…
确定边界：通过穷举分析，我们发现，当台阶数是1的时候或者2的时候，可以明确知道青蛙跳法。f（1） =1，f(2) = 2，当台阶n>=3时，已经呈现出规律f(3) = f(2) + f(1) =3，因此f（1） =1，f(2) = 2就是青蛙跳阶的边界。
找规律，确定最优子结构：n>=3时，已经呈现出规律 f(n) = f(n-1) + f(n-2) ，因此，f(n-1)和f(n-2) 称为 f(n) 的最优子结构。一道动态规划问题，其实就是一个递推问题。假设当前决策结果是f(n),则最优子结构就是要让 f(n-k) 最优,最优子结构性质就是能让转移到n的状态是最优的,并且与后面的决策没有关系,即让后面的决策安心地使用前面的局部最优解的一种性质当前在哪，可能从哪里来
写出状态转移方程：穷举分析，确定边界，最优子结构，我们就可以得出状态转移方程

需满足的条件

最优化原理：一个过程的最优决策具有这样的性质：即无论其初始状态和初始决策如何，其今后的各个策略对以第一个决策所形成的状态作为初始状态的过程而言，必须构成最优策略。也就是说一个最优策略的子策略，也是最优的。
无后效性：如果某阶段状态给定后，则在这个阶段以后过程的发展不受这个阶段以前各个状态的影响

动态规划与贪心的区别

区别
网上找的，比较好理解的

贪心算法的思路和动态规划有点不一样（个人觉得贪心算法会更简单一点）
动态规划需要枚举每一种最优解的情况（具体就如链接中的最后的凑钱问题：4+1+1、3+3）

最长上升子序列LIS

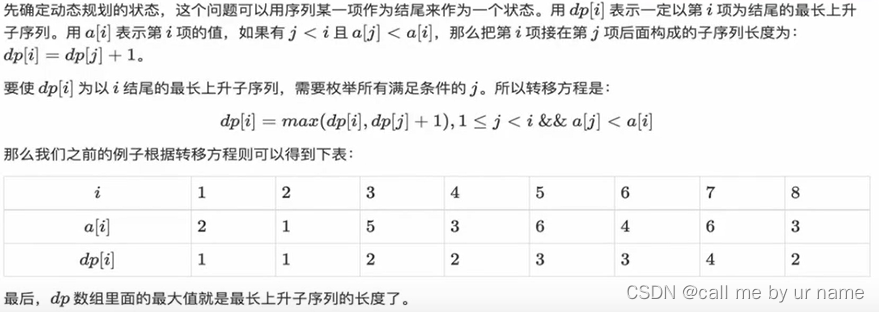
在这里插入图片描述

子序列不一定是连续的

[NOIP1999]拦截导弹

某国为了防御敌国的导弹袭击，发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。某天，雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段，所以只有一套系统，因此有可能不能拦截所有的导弹。
输入导弹依次飞来的高度（雷达给出的高度数据是不大于30000的正整数），计算这套系统最多能拦截多少导弹，如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。

输入描述

1行，若干个整数（个数≤100000）

输出描述

2行，每行一个整数，第一个数字表示这套系统最多能拦截多少导弹，第二个数字表示如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。

示例一
输入

389 207 155 300 299 170 158 65

输出

6
2

思路

题目中给出的 不能高于 ，易知：最长不上升序列
题目问的 最少要配备多少套导弹拦截系统 ：即遇到后面的比前面的大的时候（也就是不满足不上升序列），就需要加一套系统
比较基础这道题，难度低，套模板

题解

#include<bits/stdc++.h>
using namespace std;
int n=1,a[100005],dp1[100005],dp2[100005],ans1=-1,ans2=-1;
int main(){
    while(cin>>a[n]) ++n;
    for(int i=1;i<n;++i){
        dp1[i]=1,dp2[i]=1;
        for(int j=1;j<i;++j){
            if(a[i]<=a[j]) dp1[i]=max(dp1[i],dp1[j]+1); //状态转移方程
            else dp2[i]=max(dp2[i],dp2[j]+1);
        }
        ans1=max(dp1[i],ans1);
        ans2=max(dp2[i],ans2);
    }
    printf("%d\n%d",ans1,ans2);
}

状态转移方程：dp1[i] 表示的是第 i 个位置能达到的最长不上升子序列dp数组一般都是取右端点或者是终点；dp2[i] 表示的是第 i 个位置能达到的最长上升子序列

[NOIP2004 提高组] 合唱队形

$n$ 位同学站成一排，音乐老师要请其中的 $n - k$ 位同学出列，使得剩下的 $k$ 位同学排成合唱队形。

合唱队形是指这样的一种队形：设 $k$ 位同学从左到右依次编号为 $1, 2,$ … $, k$ ，他们的身高分别为 $t_1,t_2,$ … $t_k$ ，则他们的身高满足 $t_1< \cdots <t_i>t_{i+1}>$ … $>t_k(1\le i\le k)$ 。

你的任务是，已知所有 $n$ 位同学的身高，计算最少需要几位同学出列，可以使得剩下的同学排成合唱队形。

输入格式

共二行。

第一行是一个整数 $n$ （ $2\le n\le100$ ），表示同学的总数。

第二行有 $n$ 个整数，用空格分隔，第 $i$ 个整数 $t_i$ （ $130\le t_i\le230$ ）是第 $i$ 位同学的身高（厘米）。

输出格式

一个整数，最少需要几位同学出列。

样例输入 #1

8
186 186 150 200 160 130 197 220

样例输出 #1

提示

对于 $50\%$ 的数据，保证有 $\le 20$ 。

对于全部的数据，保证有 $\le 100$ 。

思路

2遍lis，从左往右最长上升，从右往左最长上升
dp[0][i]表示 i 位置（包括i）的最长上升子序列长度从左往右，dp[1][i]表示 从右往左
最后，将从左往右和从右往左相加起来-1（因为t_i计算了2次），得到最大值时，便可以知道需要减去人数的最小值

题解

#include<bits/stdc++.h>
using namespace std;
int n,a[105],ans=0,dp[2][105];
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;++i) scanf("%d",&a[i]),dp[0][i]=1,dp[1][i]=1;
    for(int i=2;i<=n;++i) for(int j=1;j<i;++j) if(a[i]>a[j]) dp[0][i]=max(dp[0][i],dp[0][j]+1);
    for(int i=n-1;i>=1;--i) for(int j=n;j>i;--j) if(a[i]>a[j]) dp[1][i]=max(dp[1][i],dp[1][j]+1);
    for(int i=1;i<=n;++i) ans=max(dp[0][i]+dp[1][i]-1,ans);
    printf("%d",n-ans);
}

最长公共子序列LCS

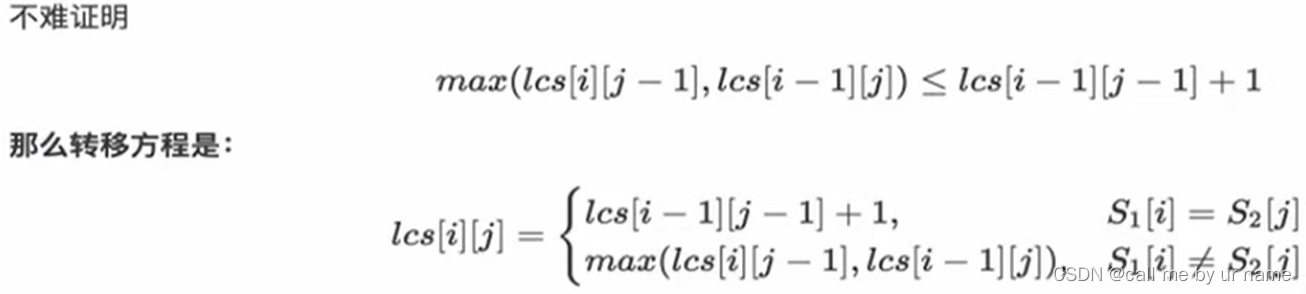
在这里插入图片描述

[HAOI2010]最长公共子序列

字符序列的子序列是指从给定字符序列中随意地（不一定连续）去掉若干个字符（可能一个也不去掉）后所形成的字符序列。
令给定的字符序列X=“x0，x1，…，xm-1”，序列Y=“y0，y1，…，yk-1”是X的子序列，存在X的一个严格递增下标序列 < i0，i1，…，ik-1 > ，使得对所有的j=0，1，…，k-1，有xij = yj。例如，X=“ABCBDAB”，Y=“BCDB”是X的一个子序列。对给定的两个字符序列，求出他们最长的公共子序列长度，以及最长公共子序列个数。

输入描述

第1行为第1个字符序列，都是大写字母组成，以”.”结束。长度小于5000。
第2行为第2个字符序列，都是大写字母组成，以”.”结束，长度小于5000。

输出描述

第1行输出上述两个最长公共子序列的长度。
第2行输出所有可能出现的最长公共子序列个数，答案可能很大，只要将答案对100,000,000求余即可。

示例一
输入

ABCBDAB.
BACBBD.

输出

4
7

思路

第一问很简单了，就是模板
第2问的分析：要求长度为 dp(i, j) 的 LCS 的个数，只需要知道长度为 dp(i, j) 转移来源的 LCS 的个数，我们就可以推出最终的答案
但是如果开2个二维数组[5005][5005]会出现MLE，占用空间过大的情况，所以要用滚动数组来优化

题解

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 5e3 + 10, mod = 1e8;
int n, m, k;
char ch, a[maxn], b[maxn];
ll f[2][maxn], g[2][maxn];
int main(){
    for (int i = 1; (ch = getchar()) != '.'; a[i] = ch, n = i, i++) ;
    getchar();
    for (int i = 1; (ch = getchar()) != '.'; b[i] = ch, m = i, i++) ;
    for (int i = 0; i <= m; i++) g[0][i] = 1; g[1][0] = 1;
    for (int i = 1; i <= n; i++, k ^= 1){
        for (int j = 1; j <= m; j++){
            g[k ^ 1][j] = 0;
            f[k ^ 1][j] = (a[i] == b[j]) ? f[k][j - 1] + 1 : max(f[k][j], f[k ^ 1][j - 1]);
            if (a[i] == b[j]) g[k ^ 1][j] += g[k][j - 1];
            if (f[k ^ 1][j] == f[k ^ 1][j - 1]) g[k ^ 1][j] += g[k ^ 1][j - 1];
            if (f[k ^ 1][j] == f[k][j]) g[k ^ 1][j] += g[k][j];
            if (f[k ^ 1][j] == f[k][j - 1]) g[k ^ 1][j] -= g[k][j - 1];
            g[k ^ 1][j] %= mod;
        }
    }
    printf("%lld\n%lld\n", f[k][m], g[k][m]);
    return 0;
}

字符串编辑距离

表示2个字符串之间，由一个字符串转化到另一个字符串所需的最少操作次数。也就是说，编辑距离越小，2个字符串的相似度越大。

在这里插入图片描述

编辑距离

设 $A$ 和 $B$ 是两个字符串。我们要用最少的字符操作次数，将字符串 $A$ 转换为字符串 $B$ 。这里所说的字符操作共有三种：

删除一个字符；
插入一个字符；
将一个字符改为另一个字符。

$A, B$ 均只包含小写字母。

输入格式

第一行为字符串 $A$ ；第二行为字符串 $B$ ；字符串 $A, B$ 的长度均小于 $2000$ 。

输出格式

只有一个正整数，为最少字符操作次数。

样例输入 #1

sfdqxbw
gfdgw

样例输出 #1

提示

对于 $\%$ 的数据， $\le |A|, |B| \le 2000$ 。

思路

模板题，难度不大，甚至没什么要注意的

题解

#include<bits/stdc++.h>
using namespace std;
char a[2005],b[2005];
int main(){
    scanf("%s%s",a,b);
    int n1=strlen(a),n2=strlen(b),dp[2005][2005];
    for(int i=1;i<=n1;++i) dp[i][0]=i;
    for(int i=1;i<=n2;++i) dp[0][i]=i;
    for(int i=1;i<=n1;++i){
        for(int j=1;j<=n2;++j){
            if(a[i-1]==b[j-1]) dp[i][j]=dp[i-1][j-1];
            else dp[i][j]=min(min(dp[i][j-1],dp[i-1][j]),dp[i-1][j-1])+1;
        }
    }
    printf("%d",dp[n1][n2]);
}

虽然纯模板题，但是在写的时候遇到了一点小问题：

用scanf()读到的 a b，起始位置是a[0]，b[0]。
而在后面 if(a[i-1]==b[j-1])这里，一开始写成了 a[i]==b[j]，没有注意到位置数组位置

序列求和问题

最大子串和

给你一个数组 a ，包含 n 个整数，你需要在其中选择连续的几个（至少一个）数，使得它们的和最大，求出最大的和。

输入描述

输出描述

输出一行，一个整数，表示最大字串和。

示例一
输入

6
1 -2 5 2 -3 5

输出

9

说明

可以选择区间[3,6]的子串，他们的和为 5+2-3+5=9

示例二
输入

8
-3 2 -3 2 2 -1 3 -2

输出

6

思路

用sum表示当前子串和，如果sum<0，就没有再继续使用这个子串和的必要了（因为，往后随便找个正数都比当前的子串和大）

题解

#include<bits/stdc++.h>
using namespace std;
int n,a[1000010],j=1;
long long sum,ans;
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++)scanf("%d",&a[i]);
    while(j<=n){
        while(sum>=0&&j<=n){   //这里的j<=n有必要，防止数组越界
            sum+=a[j++];
            ans=max(ans,sum);
        }
        sum=0;
    }
    printf("%lld",ans);
}

数字三角形

这种类型的题，能清楚地发现贪心与动态规划的区别

[USACO1.5][IOI1994]数字三角形 Number Triangles

观察下面的数字金字塔。

写一个程序来查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以走到左下方的点也可以到达右下方的点。

        7 
      3   8 
    8   1   0 
  2   7   4   4 
4   5   2   6   5

在上面的样例中,从 $\to 3 \to 8 \to 7 \to 5$ 的路径产生了最大

输入格式

第一个行一个正整数 $r$ ,表示行的数目。

后面每行为这个数字金字塔特定行包含的整数。

输出格式

单独的一行,包含那个可能得到的最大的和。

样例输入 #1

样例输出 #1

提示

【数据范围】
对于 $100\%$ 的数据， $1\le r \le 1000$ ，所有输入在 $[0, 100]$ 范围内。

思路

如果不是因为在学动态规划，那么在思考的时候可能也会想到搜索，但是对于这类题，搜索会TLE
如果是贪心的话（从上往下），在样例中，会走 $\to 8 \to 1 \to 7 \to 5$ ，但是没有题目中给出的路径和大。说明：贪心保证的是每一步的最优，但是并非总体最优。所以选择贪心算法的时候，应该要考虑每一步最优所达到的总体解是否会出现较明显的漏洞
（补充）从下往上，贪心的方法也可以。从倒数第2排开始，最左边是2，那么它往下会选择5，就将其置换为2+5=7。以此类推，倒数第3排最左边是8，其下方2个是7和12。所以8置换成20。推到第1排：7下方是23和21，选择23。得到答案30这种方法相当于做了个前缀和，考虑了路径，也可以理解为动态规划的方法吧

题解

#include<bits/stdc++.h>
using namespace std;
int n,a[1005][1005];
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;++i)for(int j=1;j<=i;++j) scanf("%d",&a[i][j]);
    for(int i=n-1;i>=1;--i){
        for(int j=1;j<=i;++j) a[i][j]+=max(a[i+1][j],a[i+1][j+1]);
    }
    printf("%d",a[1][1]);
}

矩阵相关

最大正方形

在一个 $n\times m$ 的只包含 $0$ 和 $1$ 的矩阵里找出一个不包含 $0$ 的最大正方形，输出边长。

输入格式

输入文件第一行为两个整数 $n,m(1\leq n,m\leq 100)$ ，接下来 $n$ 行，每行 $m$ 个数字，用空格隔开， $0$ 或 $1$ 。

输出格式

一个整数，最大正方形的边长。

样例输入 #1

样例输出 #1

思路

状态转移方程：f[i][j]=min(min(f[i-1][j],f[i][j-1]),f[i-1][j-1])+1
f[i][j]表示的是以数组a[i][j]为右下结点时，最大的正方形边长
当a[i][j]==1时，进行状态转移这个不多解释了。对于 min 是因为，当a[i][j]==0时，f[i][j]=0，如果不是min的话，会出现长方形

题解

#include<bits/stdc++.h>
using namespace std;
int n,m,a[105][105],f[105][105],ans=-1;
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;++i){
        for(int j=1;j<=m;++j){
            scanf("%d",&a[i][j]);
            if(a[i][j]==1) f[i][j]=min(min(f[i-1][j],f[i][j-1]),f[i-1][j-1])+1;
            ans=max(ans,f[i][j]);
        }
    }
    printf("%d",ans);
}