目录
一、二分查找的两种写法
1.1 - 第一种写法(左闭右闭)
1.2 - 第二种写法(左闭右开)
二、二分查找的六种变形
2.1 - 查找第一个 = target 的元素位置
2.2 - 查找第一个 >= target 的元素位置
2.3 - 查找第一个 > target 的元素位置
2.4 - 查找最后一个 = target 的元素位置
2.5 - 查找最后一个 <= target 的元素位置
2.6 - 查找最后一个 < target 的元素位置
三、 在排序数组中查找元素的第一个和最后一个位置
一、二分查找的两种写法
二分查找也成为折半查找(Binary Search),它是一种效率较高的查找方法。但是该方法要求待查找的序列必须是有序的,即序列中所有的元素都是按照升序(递增)或降序(递减)排列的。
二分查找的思想很简单,即选择序列中间的数字和目标值进行比较(假设序列是按升序排列的):
-
如果中间的数字小于目标值,说明包括中间数字在内的左半边区间的所有数字都小于目标值,可以全部排除。
-
如果中间的数字大于目标值,说明包括中间数字在内的右半边区间的所有数字都大于目标值,可以全部排除。
-
如果中间的数字等于目标值,则直接返回答案。
练习:704. 二分查找。
1.1 - 第一种写法(左闭右闭)
左闭右闭,即每次查找的区间为 [left, right]。
int binarySearch(int arr[], int size, int target)
{
int left = 0;
int right = size - 1;
while (left <= right)
{
int mid = (left + right) / 2;
// int mid = left + (right - left) / 2;
if (arr[mid] < target)
{
left = mid + 1;
}
else if (arr[mid] > target)
{
right = mid - 1;
}
else
{
return mid;
}
}
return -1;
}1.2 - 第二种写法(左闭右开)
左闭右开,即每次查找的区间为 [left, right),此时 arr[right] 不存在或者不符合条件。因此写法二的代码要做如下几处的修改:
-
right要初始化为size。 -
while的循环条件应该改为left < right。 -
当
arr[mid] > target时,right = mid。
int binarySearch(int arr[], int size, int target)
{
int left = 0;
int right = size;
while (left < right)
{
int mid = (left + right) / 2;
if (arr[mid] < target)
{
left = mid + 1;
}
else if (arr[mid] > target)
{
right = mid;
}
else
{
return mid;
}
}
return -1;
}二、二分查找的六种变形
2.1 - 查找第一个 = target 的元素位置
此时待查找的序列是按照非递减或者按非递增的顺序排列的,即序列中可能有重复的数字。
因此当查找序列中第一个等于 target 的元素位置时(假设序列按非递减的顺序排列),当 arr[mid] == target,也要让 right = mid - 1。
当 while 循环结束以后,判断 left 是否越界以及 arr[left] 是否等于 target,因为序列中所有的元素可能都小于 target,或者序列中并不存在等于 target 的元素。
如果 left 既没有越界,arr[left] 又等于 target,则 left 就是第一个等于 target 的元素位置。
理解方式一:
此时 arr[right] <= target:
-
若
arr[right] < target,则说明mid,即 right + 1就是第一个 = target 的元素位置,当 while 循环结束以后,left等于mid。 -
若
arr[right] == target,则说明mid不是第一个 = target 的元素位置,而可能是当前的 right 或者是更之前的位置。
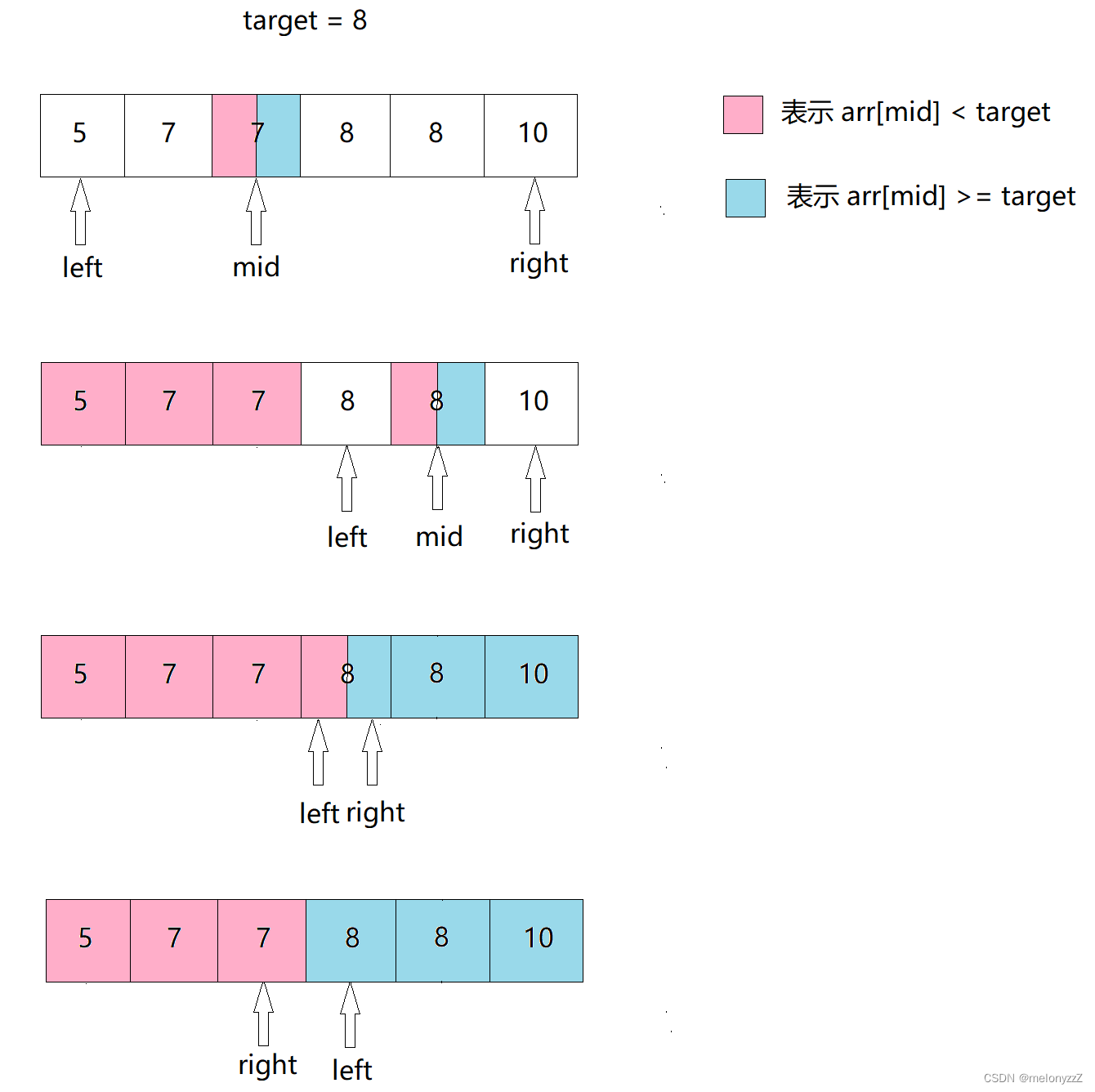
理解方式二:
当 while 循环结束以后(left > right):
-
left 左边的元素都小于 target。
-
right 右边的元素都大于或等于 target。
所以此时 right + 1,即 left 就可能是第一个等于 target 的元素位置(因为也有可能是大于 target 的元素位置)。
int firstEq(int arr[], int size, int target) // Eq:Equal to
{
int left = 0;
int right = size - 1;
while (left <= right)
{
int mid = (left + right) / 2;
if (arr[mid] < target)
{
left = mid + 1;
}
else // arr[mid] >= target
{
right = mid - 1;
}
}
if (left < size && arr[left] == target)
return left;
return -1;
}
2.2 - 查找第一个 >= target 的元素位置
和查找第一个等于 target 的元素位置不同在于,当 while 循环结束以后不需要判断 left 是否越界以及 arr[left] 是否等于 target,如果序列中所有的元素都比 target 小,则返回序列的长度。
int firstGE(int arr[], int size, int target) // GE:Greater than or Equal to
{
int left = 0;
int right = size - 1;
while (left <= right)
{
int mid = (left + right) / 2;
if (arr[mid] < target)
{
left = mid + 1;
}
else // arr[mid] >= target
{
right = mid - 1;
}
}
return left;
}2.3 - 查找第一个 > target 的元素位置
int firstGt(int arr[], int size, int target) // Gt:Greater than
{
int left = 0;
int right = size - 1;
while (left <= right)
{
int mid = (left + right) / 2;
if (arr[mid] <= target)
{
left = mid + 1;
}
else // arr[mid] > target
{
right = mid - 1;
}
}
return left;
}2.4 - 查找最后一个 = target 的元素位置
int lastEq(int arr[], int size, int target) // Eq:Equal to
{
int left = 0;
int right = size - 1;
while (left <= right)
{
int mid = (left + right) / 2;
if (arr[mid] <= target)
{
left = mid + 1;
}
else // arr[mid] > target
{
right = mid - 1;
}
}
if (right >= 0 && arr[right] == target)
return right;
return -1;
}2.5 - 查找最后一个 <= target 的元素位置
int lastLE(int arr[], int size, int target) // LE:Less than or Equal to
{
int left = 0;
int right = size - 1;
while (left <= right)
{
int mid = (left + right) / 2;
if (arr[mid] <= target)
{
left = mid + 1;
}
else // arr[right] > target
{
right = mid - 1;
}
}
return right;
}2.6 - 查找最后一个 < target 的元素位置
int lastLt(int arr[], int size, int target) // Lt:Less than
{
int left = 0;
int right = size - 1;
while (left <= right)
{
int mid = (left + right) / 2;
if (arr[mid] < target)
{
left = mid + 1;
}
else // arr[mid] >= target
{
right = mid - 1;
}
}
return right;
}三、 在排序数组中查找元素的第一个和最后一个位置
题目描述:
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]
示例 3:
输入:nums = [], target = 0
输出:[-1,-1]
提示:
-
0 <= nums.length <= 10^5 -
-10^9 <= nums[i] <= 10^9 -
nums是一个非递减数组 -
-10^9 <= target <= 10^9
代码实现:
int firstGE(int nums[], int numsSize, int target)
{
int left = 0;
int right = numsSize - 1;
while (left <= right)
{
int mid = (left + right) / 2;
if (nums[mid] < target)
{
left = mid + 1;
}
else // nums[mid] >= target
{
right = mid - 1;
}
}
return left;
}
int* searchRange(int* nums, int numsSize, int target, int* returnSize)
{
*returnSize = 2;
int* ans = (int*)malloc(sizeof(int) * 2);
int start = firstGE(nums, numsSize, target);
// start 为数组中第一个大于或等于 target 的元素位置
if (start == numsSize || nums[start] != target)
{
ans[0] = -1;
ans[1] = -1;
return ans;
}
// 因为 nums 是整型数组,所以查找最后一个小于或等于 target 的元素位置,
// 可以转换为查找第一个大于或等于 target + 1 的元素位置,然后将得到的结果减去 1。
// start 存在,则 end 必定存在,且 nums[end] 就等于 target。
int end = firstGE(nums, numsSize, target + 1) - 1;
ans[0] = start;
ans[1] = end;
return ans;
}