二叉树性质
满二叉树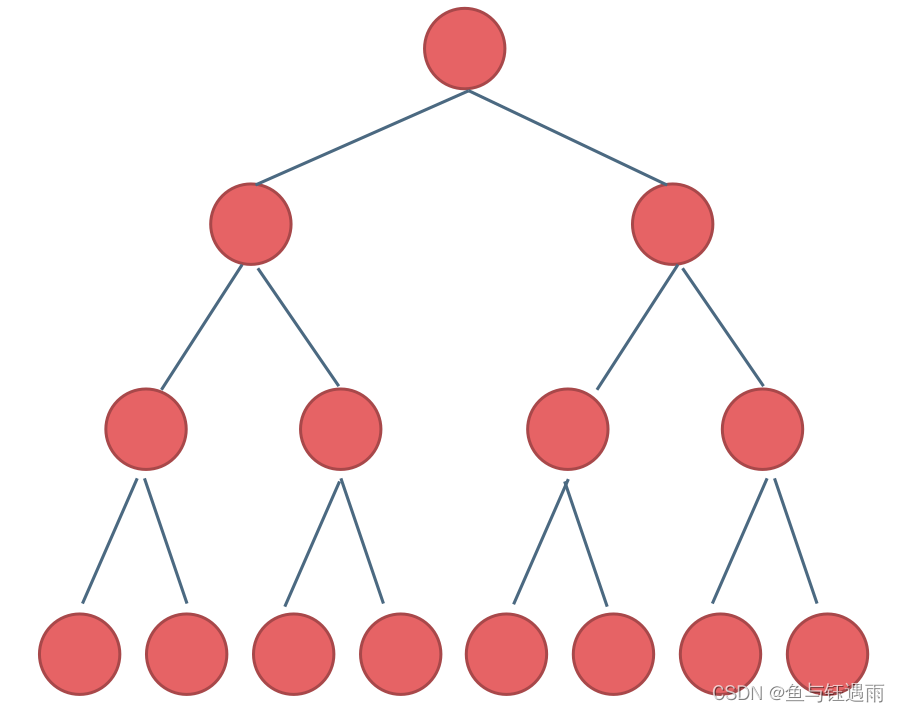
深度为k,有 2 k − 1 2^{k}-1 2k−1个结点的二叉树,为满二叉树。
完全二叉树
完全二叉树的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2^(h-1) 个节点。
二叉树的存储方式
包括链式存储和顺序存储
由于链式存储的二叉树更有利于我们理解,所以我们一般都是用链式存储二叉树。
所以大家要了解,用数组依然可以表示二叉树。
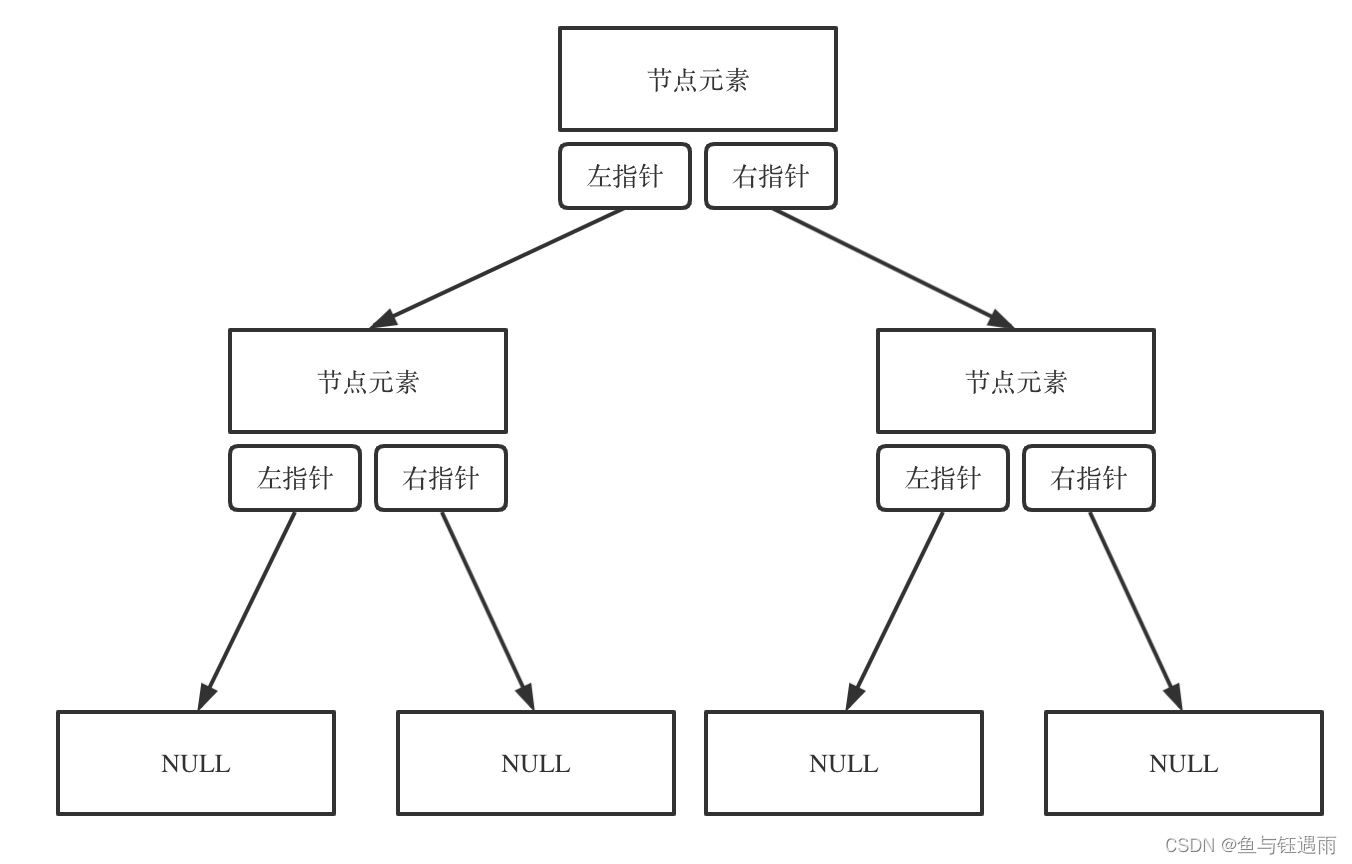
二叉树链式存储代码
struct TreeNode{
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x):val(x),left(NULL),right(NULL){}
};
二叉树的遍历方式
遍历方式分两类,四种
关于二叉树的遍历方式,首先从深度和广度来区分。
- 深度优先遍历:先往深走,遇到叶子节点再往回走。
- 广度优先遍历:一层一层地去遍历。
这两种遍历是图论中最基本的两种遍历方式,后面在介绍图论的时候,还会介绍到。
那么我们进一步扩展深度优先遍历和广度优先遍历,才会有更为细致的遍历方式的区分:
- 深度优先遍历
- 前序遍历(递归法,迭代法)
- 中序遍历(递归法,迭代法)
- 后序遍历(递归法,迭代法)
- 广度优先遍历
- 层次遍历(迭代法)
在深度优先遍历中:有三个顺序,前中后序遍历,有同学总分不清这三个顺序,经常搞混,我这里教大家一个技巧。
这里前中后,其实指的就是中间节点的遍历顺序,只要大家记住,前中后序指的就是中间节点的位置就可以了。看如下节点的遍历顺序,就可以发现中间节点的顺序就是所谓的遍历方式名称的由来:
- 层次遍历(迭代法)
- 前(先)序遍历:中左右
- 中序遍历:左中右
- 后序遍历:左右中
遍历方式的实现
最后再说一说二叉树中深度优先遍历和广度优先遍历的实现方式。我们做二叉树相关的题目,经常会使用递归的方式来实现深度优先遍历。
之前讲栈的时候,说过栈其实就是递归的一种实现结构,先进后出。也就就是说前中后序遍历的逻辑其实都是可以借助栈使用非递归的方式来实现。(通过栈的结构避免了递归操作)
而广度优先遍历的实现,一般借助队列来实现,这也是由于队列先进先出的特点所决定的,因为需要先进先出的结构,才能一层一层的来遍历二叉树。
这里其实我们又了解了栈与队列的一个应用场景了。
具体的实现我们后面都会讲的,这里大家先要清楚这些理论基础。
二叉树与递归(二叉树的递归遍历)
说到二叉树,就不得不说递归,很多同学对递归都是又熟悉又陌生,递归的代码一般很简短,但每次都是一看就会,一写就废。
递归写不好的根本原因就是不成体系,没有递归方法论。通过二叉树的前中后序的递归写法,我们把递归方法论确定下来,进而应对复杂的递归题目。
首先,每次写递归算法,先确定三要素:
- 确定递归函数的参数和返回值: 确定哪些参数是递归的过程中需要处理的,那么就在递归函数里加上这个参数, 并且还要明确每次递归的返回值是什么进而确定递归函数的返回类型。
- 确定终止条件: 写完了递归算法, 运行的时候,经常会遇到栈溢出的错误,就是没写终止条件或者终止条件写的不对,操作系统也是用一个栈的结构来保存每一层递归的信息,如果递归没有终止,操作系统的内存栈必然就会溢出。
- **确定单层递归的逻辑:**确定每一层递归需要处理的信息。在这里也就会重复调用自己来实现递归的过程。
那三要素怎么切入,怎么找呢?
我们以前序遍历为例子,来找感觉!
1.确定递归函数的参数和返回值:因为我们要打印前序遍历节点的数值,因此参数里需要传入vector来放节点的数值,除了这一点就不需要再处理什么数据了,也不需要有返回值,所以递归函数返回类型就是void,代码如下:
(代码随想录点评:为什么要传入vector没讲清楚,另外代码还传入了节点本身,也很令人困惑?因为后面说的是除了vector不需要再处理什么数据了,也不需要有返回值,但是没提到传入TreeNode *cur的目的,但是我的猜想是,对树本身进行处理,肯定是要传入当前处理的树节点的指针的,至于为什么一定要用vector来放节点的数值,我想不通,希望后面会想通)
void traversal(TreeNode* cur, vector<int>& vec)
2.确定终止条件:在递归过程中,如何算递归结束?对于前序遍历,如果当前遍历的节点是空了,就说明递归结束了,所以如果当前遍历的节点是空,就直接return,代码如下:
if (cur == NULL) return;
3.确定单层递归的逻辑:前序遍历是中左右的顺序,因此单层递归的逻辑就是,先取中点节点的数值,(单层递归的逻辑这个概念讲的也不通!! 首先,什么是单层递归?如果重复调用单层递归实现递归的过程? 我的理解就是,每读到一个新数据,应当怎么处理这个数据,这个就是单层递归的数据处理逻辑!!!数据处理完成之后,就到了递归的逻辑了,单层递归本质上在数据处理完之后就结束了!!!后面就是递归的逻辑,例如这里递归下一个处理的数据是左子树的节点,因此对左子树进行递归,然后处理右子树,这里就继续对右子树进行递归!! 因此这里所说的单层递归,本质上就是一次数据处理过程+后面需要继续递归的数据!!!)
因此,代码如下
vec.push_back(cur->val); // 中
traversal(cur->left, vec); // 左
traversal(cur->right, vec); // 右
到这,我仍然看不懂,原因在于,我不知道TreeNode* cur的意义,以及vector &vec的意义,这就是代码随想录这一部分的败笔,读者很难理解!!!
然而,当读者继续往下读,读到整体代码的时候,就会恍然大悟:
class Solution {
public:
void traversal(TreeNode* cur, vector<int>& vec) {
if (cur == NULL) return;
vec.push_back(cur->val); // 中
traversal(cur->left, vec); // 左
traversal(cur->right, vec); // 右
}
vector<int> preorderTraversal(TreeNode* root) {
vector<int> result; //vector就是我们的遍历结果存储向量
traversal(root, result);//遍历需要输入树的根节点
return result;
}
};
vector就是我们的遍历结果存储向量;遍历需要根据树逐步往下走,因此需要传入树根,并根据树根往下走,因此需要传入TreeNode* cur这参数。