随着人工智能技术的不断发展,越来越多的领域开始应用自动化技术来提高工作效率和减少人工干预。对于表格中的文字识别和录入,目前已经有一些技术可以实现自动化,下面是一些可能的方法:
一、图片类表格文字自动识别并录入解决方案
(1)、有规律及固定模板、样式的图片表格文字,如证件、票据、银行卡、名片等。
这类图片可以用眼精星证票识别系统来将其转为结构化数据,可以自定义想要的字段,以名片识别来例,我们来谈谈它实现和操作的步骤:
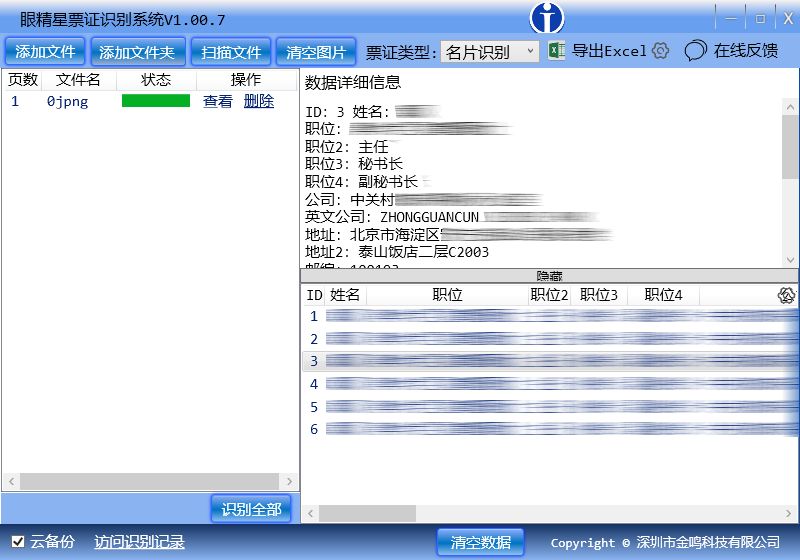
请点击输入图片描述(最多18字)
1. 打开眼精星票证识别系统,在票证类型处选择“名片”。
2. 将需要识别的纸质名片用扫描仪扫描或用手机等摄影器材拍照成图。
3. 将待识别的名片图片添加到程序列表
4. 点击“识别全部”按钮,等待系统处理完毕。
5. 系统会自动将名片中的姓名、电话、邮箱等关键信息提取出来,形成结构化的数据。
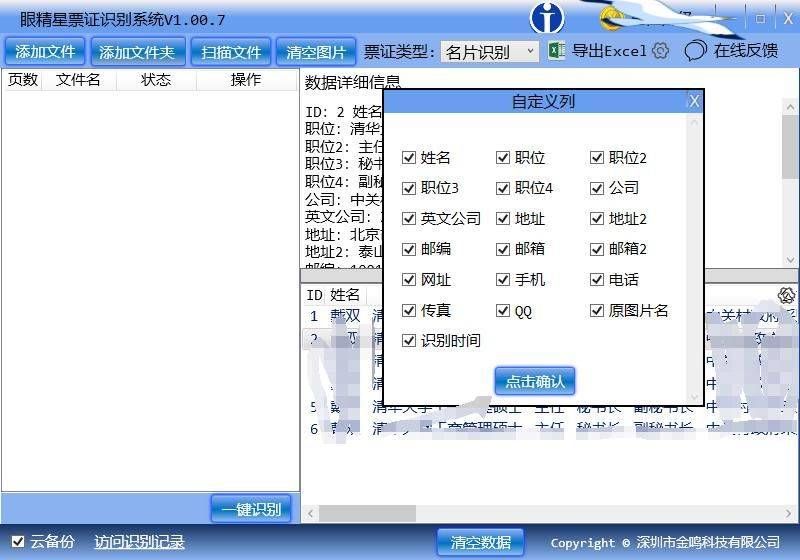
6. 在眼精星票证识别系统中,点击“导出excel”按钮。
7. 点击旁边的图标,可设置需导出的列名(字段名),如不设置,默认为导出全部字段。
8. 导出完成后可自动打开excel文档。
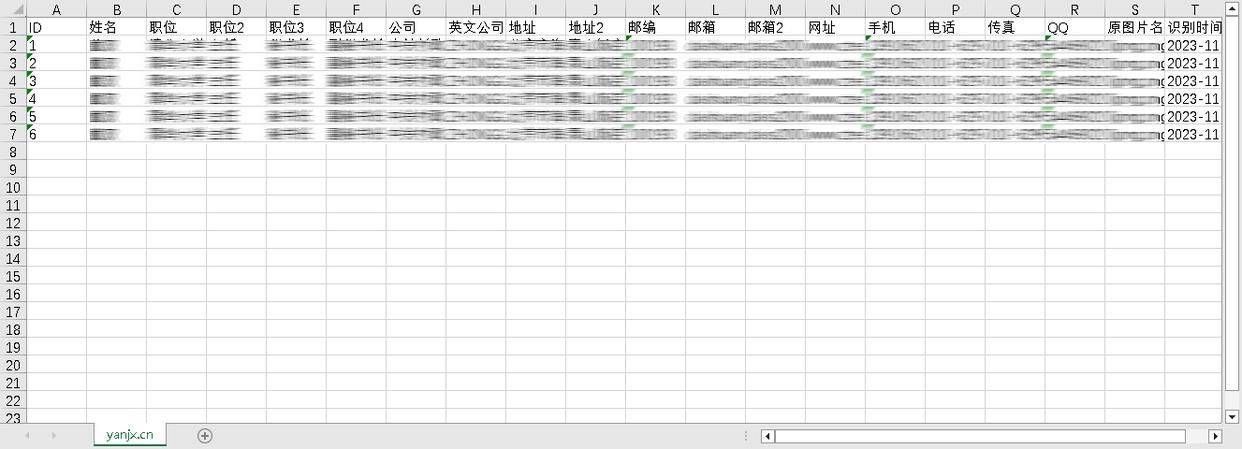
(2)、无规律、无固定模板的图片表格
这类图片只能用如金鸣识别的通用表格识别模块,将它转成excel,然后再编辑处理成符合自己需求的文档。
二、文本类表格
这类表格中的文字已是文本,我们就无需再用到OCR软件了,如果想省事一点,我们可以用以下人工智能技术来处理。
 1.自然语言处理(NLP)技术
1.自然语言处理(NLP)技术
NLP技术是一种让计算机理解和处理自然语言的技术。通过使用深度学习等算法,NLP技术可以对文本进行自动分类、实体识别、情感分析等操作。对于表格中的文字识别,可以使用NLP技术来提取表格中的关键信息,并将其自动录入到系统中。
2.智能模板匹配技术
智能模板匹配技术是一种基于预先定义的模板和算法来自动匹配和填写表格信息的技术。该技术可以通过对表格结构和数据的分析,自动识别和填写表格中的关键信息,如姓名、地址、电话等。使用智能模板匹配技术可以大大减少人工干预和录入时间。
3.智能表单技术
智能表单技术是一种结合了OCR、NLP、智能模板匹配等技术,实现自动识别和填写表单的技术。通过智能表单技术,用户只需要将表单拍照或扫描,系统即可自动识别和填写表单中的信息,大大提高了工作效率和准确性。
以上是几种可能的方法来实现表格中文字的自动识别和录入。需要注意的是,不同的方法适用于不同的应用场景和数据类型,需要根据实际情况选择合适的方法来实现自动化。同时,在使用自动化技术时,也需要考虑到数据隐私和安全等方面的问题,确保数据的安全性和合规性。

![P6354 [COCI2007-2008#3] TAJNA](https://img-blog.csdnimg.cn/img_convert/fcb815275ab384982b95ad50976c9e3d.png)