题目传送门

题目描述

使用一种加密算法。

设字符串的长度为 n，则构造一个矩阵，使得 r×c=n 且在 r≤c 的情况下使得 r 尽量大。

然后把给定的明文按照由上到下，从左到右的顺序填充这个 r×c 的矩阵。

得到的密文就是把矩阵按照从左到右，从上到下的顺序输出的字符串。

给定你明文，请你输出密文。

输入格式

一行一个字符串，表示明文。

输出格式

一行一个字符串，表示密文。

输入输出样例

输入 #1

bok

输出 #1

bok

输入 #2

koaski

输出 #2

kakosi

输入 #3

boudonuimilcbsai

输出 #3

bombonisuuladici

说明/提示

样例 3 解释

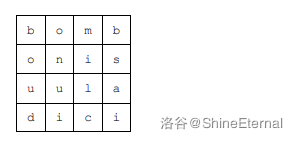
共 16 个字符，对于矩阵的长宽，可以选择 1×16，2×8 和 4×4 这三种，因为要求 r 尽量大，所以选择 4×4。

然后进行填充，填充的结果如上图所示。

最后从左到右，从上到下输出每个字符即可。

数据规模与约定

对于 100% 的数据，保证输入字符串只含小写字母，长度不超过 100。

说明

题目译自 COCI2007-2008 CONTEST #3 T3 TAJNA。

思路 

首先输入密文 s，s 是一个 string 类型

长度 l 用  .size() 函数计算，因为要使 r 尽可能大，则让 r 从 sqrt(l)​ 开始，依次减一

使用数组 存储矩阵

#include<bits/stdc++.h>
using namespace std;
string s;
int r,c;
char a[110][110];
int main()
{
    cin>>s;
    int l=s.size();
    for(int i=sqrt(l);i>0;i--)
    {
        if(l%i==0)
        {
            r=i;
            c=l/i;
            break;
        }
    }
    int t=0;
    for(int i=0;i<c;i++)
    {
        for(int j=0;j<r;j++)
        {
            a[j][i]=s[t];
            t+=1;
        }
    }
    for(int i=0;i<r;i++)
    {
        for(int j=0;j<c;j++)
        {
            cout<<a[i][j];
        }
    }
    return 0;
}

 如有错误，欢迎大家评论区指出！感谢！