前言：感谢您的关注哦，我会持续更新编程相关知识，愿您在这里有所收获。如果有任何问题，欢迎沟通交流！期待与您在学习编程的道路上共同进步。

 

 

目录

一.  独立按键灵活控制LED 

程序一：单个独立按键控制多个LED灯

程序二：多个独立按键同时控制LED 

二.  独立按键实现LED的位移控制 

1.位运算介绍：

2.具体运用：

三.  实验视频 

 

---

 

一.  独立按键灵活控制LED 

 

  对于独立按键的具体介绍可以参考：51单片机学习（3），这里我们借助一些算术运算符以及一些逻辑运算符来实现不同的控制。

运算符如下：

 

 

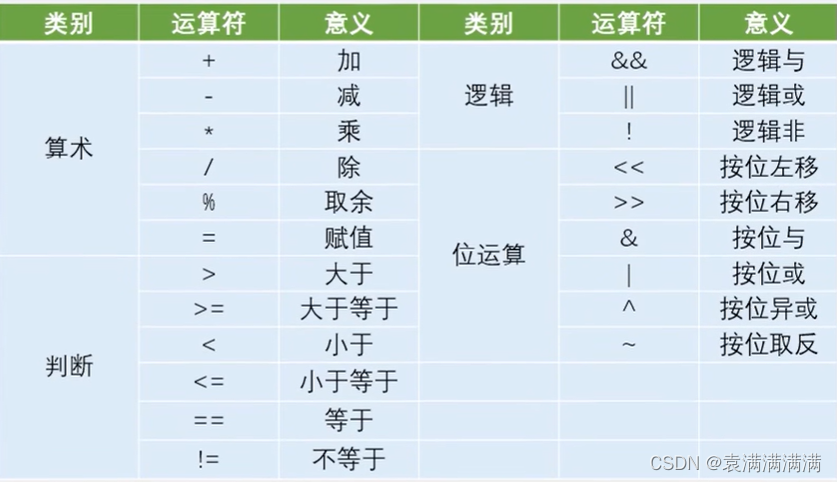
例如：

程序一：单个独立按键控制多个LED灯

#include <REGX52.H>

void Delay(unsigned int xms)	//@11.0592MHz
{
	unsigned char data i, j;
	while(xms)
	{
		i = 2;
		j = 199;
		do
		{
			while (--j);
		} while (--i);
		xms--;
	}
}
void main()
{
	while(1)
	{
			if(P3_1==0)
		{
			Delay(20);
			while(P3_1==0);
			Delay(20);
			P2_0=~P2_0, P2_1=~P2_1;  //实现K1控制LED1和LED2
		}
	}
}

 

程序二：多个独立按键同时控制LED 

#include <REGX52.H>

void Delay(unsigned int xms)	//@11.0592MHz  //延时函数设置
{
	unsigned char data i, j;
	while(xms)
	{
		i = 2;
		j = 199;
		do
		{
			while (--j);
		} while (--i);
		xms--;
	}
}
void main()
{
	while(1)   //while循环语句
	{
		if(P3_1==0||P3_0==0)   //if语句，并且运用逻辑或
		{
			Delay(20);    //延时20ms，去除第一段抖动
			while(P3_1==0||P3_0==0);
			Delay(20);  //去除第二段抖动
			P2_0=~P2_0;   //按位取反，即对应的LED状态改变
		}
	}
}

 

二.  独立按键实现LED的位移控制 

 

1.位运算介绍：

按位与（&）： 按位与为双位运算符，其作用于将两个二进制数逐位相与，即只要对应的两个二进制都为1时，结果为1，否则为0。

例如：1&1=1，1&0=0，0&0=0。

按位或（|）：按位或也为双目运算符，其作用于将两个二进制数逐位相或，即只要对应的两个二进制中有一个为1，其结果为1，否则为0。

例如：1|1=1，1|0=1，0|0=0。

按位异或（^）：进行异或运算时，当两个二进制表示不同时为1，相同则为0。

例如：1^1=0，1^0=1。

按位取反（~）：按位取反即对于二进制的每一位都取反。

例如：假设1的二进制为0000 0001，则按位取反后为1111 1110。

按位左移（<<）：将操作数的二进制所有位向左移动指定的位数。

例如：1的二进制0000 0001，0000 0001<<2即1的二进制数按位左移动2位，则为0000 0100。

按位右移（>>）：将操作数的二进制所有位向左移动指定的位数。

例如：10的二进制为0000 1010，0000 1010>>2即10的二进制数按位右移动2位，则为0000 0010（右移两位时高位补0即右移后的第一位补0）。

注意：这里的按位左移与右移均只对于正数而言，且左移时为低位补0，右移时为高位补0。

 

2.具体运用：

源程序：

#include <REGX52.H>
void Delay(unsigned int xms)	//@11.0592MHz
{
	unsigned char data i, j;
	while(xms)
	{
		i = 2;
		j = 199;
		do
		{
			while (--j);
		} while (--i);
		xms--;
	}
}

void main()
{
	unsigned int LEDNUM=0;  //定义移动的位数
	while(1)
	{
		if(P3_1==0)
		{
			Delay(20);
			while(P3_1==0);
			Delay(20);
			LEDNUM++;   //移动的位数逐渐增加来实现逐次控制不同LED
			if(LEDNUM>=8)
			{
				LEDNUM=0;   //当移动的位数超过8时重新令位数为0，从而实现不断的逐次循环
			}
			P2=~(0x01<<LEDNUM);  //0x01本应该是第一个LED亮，但是这里马上进行了位运算，所以第一个点亮的为第二个LED然后依次被控制点亮。
		}
	}
}

 

三.  实验视频 

 

感谢老铁的浏览，希望老铁可以一键三连加个关注，您的支持和鼓励是我前进的动力，后续会分享更多学习编程的内容。