目录

欧拉函数

快速幂算法

快速模幂算法

---

欧拉函数

两个不同的正整数a,b，若gcd(a,b)=1,则a和b互质，1与任何正整数都互质

欧拉函数的意义

φ(n) 表示小于或等于正整数n的所有正整数中与n互质的数的个数

如φ(32) =16，即小于32的数中有16个与32互质的数，分别是

 1、3、5、7、9、11、13、15、17、19、21、23、25、27、29、31

任何正整数都可以表示成若干个素数的乘积，即写成如下形式

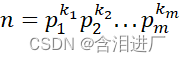
p表示素因子，k表示该素因子个数

欧拉函数的性质

(1)若p 为素数，则有

φ(p)=p-1

(2)若m 和n 互质，则有

φ(mn)=φ(m)φ(n)

(3)分解公式

(4)若n%m=0 且%m=0,则有

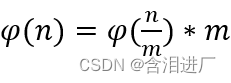
特殊地，令m=a^(b-1) ，n=a^b ，则可以得到

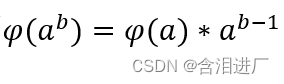
利用该定理可以用来求大指数的欧拉函数值

(5)若和m互质，且m为素数 ，则有

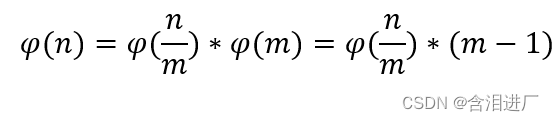
(6)费马定理：若gcd(a,p)=1 ，则有

由分解公式求数a的欧拉函数值

​
pri = []  # 存储a的所有素因子
e = a
for i in range(2, int(e ** 0.5) + 1):  # int会下取整，所以最后加上1防止误差
    if e % i == 0:
        pri.append(i)
        while e % i == 0:  # 找到一个因子就用这个数一直除以该因子，消除该因子，保证后面找到的因子都是素因子
            e = e // i

if e != 1:  # 如果最后除出来结果不是1，说明还剩个素因数
    pri.append(e)

for p in pri:# 遍历a的所有素因子
    a = a // p * (p-1) 

print(a)#最后的a即为欧拉函数值

​

快速幂算法

求a^n  其中n>0

以3^13为例，13的二进制为1101，因此3的13次方可以分解成以下形式：

将指数进行二进制分解，然后按二进制从右到左的顺序即倒回来遍历，如果二进制为1，则进行乘法运算,需要乘2^(i-1) ，i 表示第几位

由于1的二进制除了最低位是1，其他的全是0，因此可以利用n&1来判断n的二进制的最低位是否为1，如果n&1等于1，说明当前n的最低位是1，需要乘底数，反之n的最低位是0不用进行乘法，然后将n使用>>进行右移一位，产生新的最低位，直到n所有位数都移完，a在每次循环后都要进行平方更换为新底数

def fun(a, n):  # 底数，指数
    result = 1
    while n != 0:
        if (n & 1) == 1:
            result = result * a
        n = n >> 1
        a = a ** 2  # 将a重新赋值为a平方
    return result

直接使用暴力求幂的话时间复杂度为O(n)，而使用快速模幂算法时间复杂度为O(log2⁡n)

快速模幂算法

模运算规则

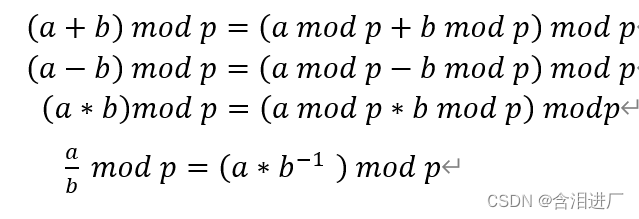
其中b-1  是b 模p 的逆元，在python可以用内置函数pow求逆元， pow(a,b,p) 表示a^b mod p

所以pow(a,-1,p) 就是a 模p 的逆元

也可以由费马定理求逆元：由费马定理b^(p-1) mod p=1 可得

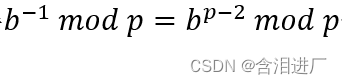
求b^(p-2) mod p可以使用快速模逆算法，根据模运算的乘法法则，方法跟快速幂算法差不多，只不过多了模数

def fun(a, n, m):  # 底数，指数，模数
    result = 1
    while n != 0:
        if (n & 1) == 1:
            result = (result * a) % m
        n = n >> 1
        a = (a ** 2) % m  # 将a重新赋值为a平方
    return result