解法一：字典树
前置知识：字典树
字典树是一种实现字符串快速检索的多叉树结构。
例如：给定字符串集合[cab, cos, car, cat], 我们现在需要判断cat是否存在于字符串集合中。
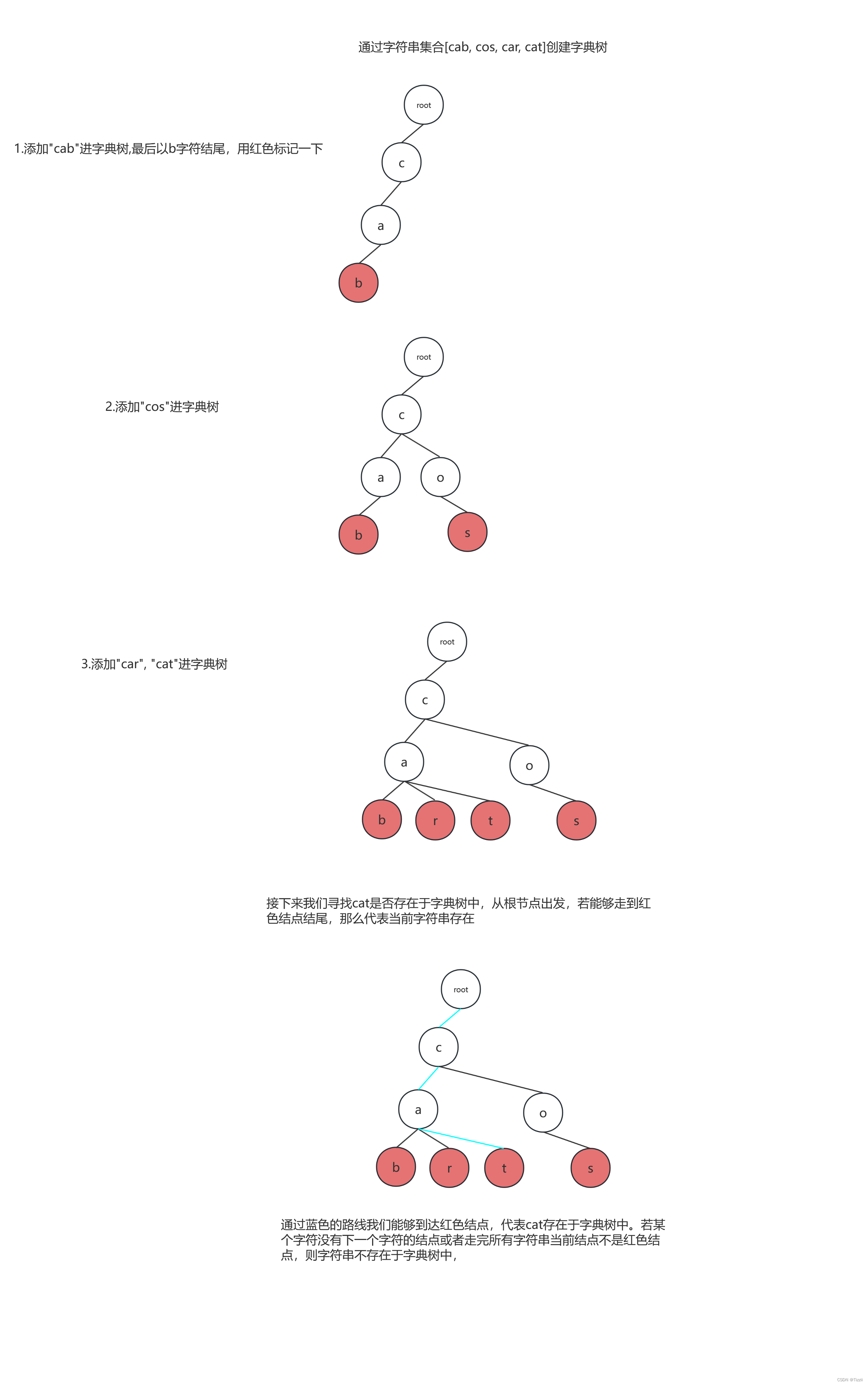字典树代码：
static int[][] trie = new int[N][26]; //其中N为结点个数，一般为所有字符串长度之和。
static int[] cnt = new int[N]; //代表红色结点结尾出现的次数
void add(String str) { //将字符串str添加进字典树
int p = 0; //根结点为0号
for (char c : str.toCharArray()) {
int u = c - 'a';
if (trie[p][u] == 0) trie[p][u] = ++idx; //创建结点并赋予编号idx
p = trie[p][u]; //走到下一个结点
}
cnt[p]++; //个数增加
}
static int query(String str) {
int p = 0;
for (char c : str.toCharArray()) {
int u = c - 'a';
if (trie[p][u] == 0) return 0; //若当前结点不存在，那么直接返回0
p = trie[p][u];
}
return cnt[p];
}
int trie[N][26], cnt[N], idx;
void insert(string str){
int p = 0;
for (int i = 0; i < str.length(); i++){
int u = str[i] - 'a';
if (!trie[p][u]) trie[p][u] = ++ idx;//创建结点并赋予编号idx
p = trie[p][u];//走到下一个结点
}
cnt[p]++ ;//个数增加
}
int query(string str){
int p = 0;
for (int i = 0; i < str.length(); i++){
int u = str[i] - 'a';
if (!trie[p][u]) return 0; //若当前结点不存在，那么直接返回0
p = trie[p][u];
}
return cnt[p];//返回存在的次数
}
动态开辟结点：
class Trie {
Trie[] trie = new Trie[26];
int cnt;
}
Trie root = new Trie();
void add(String str) {
Trie p = root;
for (char c : str.toCharArray()) {
int u = c - 'a';
if (p.trie[u] == null) p.trie[u] = new Trie(); //创建结点
p = p.trie[u];
}
p.cnt++; //个数增加
}
int query(String str) {
Trie p = root;
for (char c : str.toCharArray()) {
int u = c - 'a';
if (p.trie[u] == null) return 0;
p = p.trie[u];
}
return p.cnt;
}
- 相关题目：208. 实现 Trie (前缀树) 421. 数组中两个数的最大异或值，建议不熟悉字典树的先将这两道题目做一下。
回到本题，我们要求
(
i
,
j
)
(i, j)
(i,j) 的数对使得
l
o
w
<
=
(
n
u
m
s
[
i
]
X
O
R
n
u
m
s
[
j
]
)
<
=
h
i
g
h
low <= (nums[i]\ XOR\ nums[j]) <= high
low<=(nums[i] XOR nums[j])<=high。首先对于每个数字，我们可以通过二进制来表示，由于
n
u
m
s
[
i
]
≤
2
∗
1
0
4
nums[i]\leq 2 * 10^4
nums[i]≤2∗104,因此15位二进制就可以进行表示。对于某个数x = 3,二进制表示“000000000000011”， 我们将该串存入字典树中。
题目需要求异或值在
[
l
o
w
.
h
i
g
h
]
[low. high]
[low.high]之间的数，直接求解不太好求解，我们可以通过容斥原理转化一下，求解
a
n
s
=
≤
h
i
g
h
ans\ =\ \leq high
ans = ≤high的对数 -
≤
(
l
o
w
−
1
)
\leq (low-1)
≤(low−1)的对数。
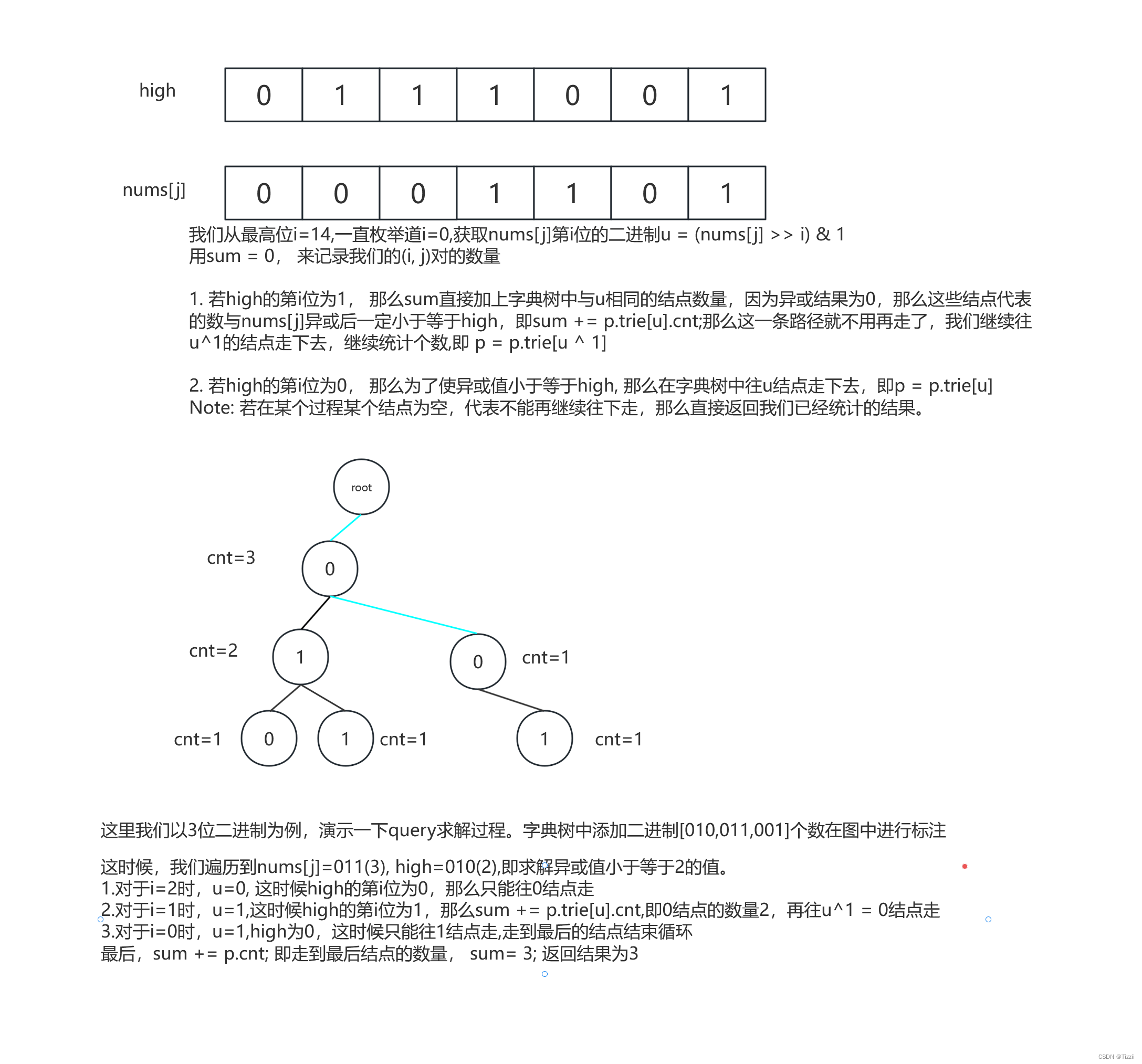
如何在字典树中求解
(
i
,
j
)
(i,j)
(i,j)对的异或值小于等于
h
i
g
h
high
high?
首先，
i
<
j
i < j
i<j, 对于某个j来说，我们将之前
[
1
,
j
−
1
]
[1,j-1]
[1,j−1]的数存入字典树中，在实现
a
d
d
(
)
add()
add()方法时，我们对每一个结点都统计其出现的位置，方便我们后面计算个数。当
[
1
,
j
−
1
]
[1,j-1]
[1,j−1]的数都添加进字典树后，我们进行一次查询
q
u
e
r
y
(
)
query()
query()返回
≤
h
i
g
h
\leq high
≤high的异或对数量。
- 时间复杂度： O ( n l o g m ) O(nlogm) O(nlogm), 其中m为最大的数
- 空间复杂度： O ( n l o g m ) O(nlogm) O(nlogm),开辟结点数量
class Solution {
int[][] trie;
int[] cnt;
int idx;
public int countPairs(int[] nums, int low, int high) {
trie = new int[nums.length * 16][2];
cnt = new int[nums.length * 16];
return get(nums, high) - get(nums, low - 1);
}
int get(int[] nums, int high) {
idx = 0;
for (int i = 0; i < trie.length; i++) trie[i][0] = trie[i][1] = cnt[i] = 0;
int ans = 0;
for (int i = 0; i < nums.length; i++) {
ans += query(nums[i], high);
add(nums[i]);
}
return ans;
}
void add(int x) {
int p = 0;
for (int i = 14; i >= 0; i--) {
int u = (x >> i) & 1;
if (trie[p][u] == 0) trie[p][u] = ++idx;
p = trie[p][u]; //移动到下一个结点
cnt[p]++; // 个数增加，cnt[x]代表x结点出现的次数
}
}
int query(int x, int high) {
int sum = 0, p = 0;
for (int i = 14; i >= 0; i--) {
int u = (x >> i) & 1;
if (((high >> i) & 1) == 1) { //high当前i位为1, 那么x与以前数当前i位的异或可以位1或者0
sum += cnt[trie[p][u]];//加上与x异或后当前i位为0的数量
if (trie[p][u ^ 1] == 0) return sum; //没有结点可以继续走下去，直接返回
p = trie[p][u ^ 1]; //继续往异或的结点走下去
} else { //high当前i位为0, x与以前数异或的第i为必须为0
if (trie[p][u] == 0) return sum; //没有结点走下去
p = trie[p][u]; //寻找与x的第i位相同的进制，异或结果为0
}
}
sum += cnt[p]; //加上走到最后的结点数
return sum;
}
}
const int N = 20005;
int trie[N * 15][2], cnt[N * 15], idx;
class Solution {
public:
int countPairs(vector<int>& nums, int low, int high) {
return get(nums, high) - get(nums, low - 1);
}
int get(vector<int>& nums, int high) {
idx = 0;
memset(trie, 0, sizeof(trie));
memset(cnt, 0, sizeof(cnt));
int ans = 0;
for (int i = 0; i < nums.size(); i++) {
ans += query(nums[i], high);
add(nums[i]);
}
return ans;
}
void add(int x) {
int p = 0;
for (int i = 14; i >= 0; i--) {
int u = (x >> i) & 1;
if (trie[p][u] == 0) trie[p][u] = ++idx;
p = trie[p][u]; //移动到下一个结点
cnt[p]++; // 个数增加，cnt[x]代表x结点出现的次数
}
}
int query(int x, int high) {
int sum = 0, p = 0;
for (int i = 14; i >= 0; i--) {
int u = (x >> i) & 1;
if (((high >> i) & 1) == 1) { //high当前i位为1, 那么x与以前数当前i位的异或可以位1或者0
sum += cnt[trie[p][u]];//加上与x异或后当前i位为0的数量
if (trie[p][u ^ 1] == 0) return sum; //没有结点可以继续走下去，直接返回
p = trie[p][u ^ 1]; //继续往异或的结点走下去
} else { //high当前i位为0, x与以前数异或的第i为必须为0
if (trie[p][u] == 0) return sum; //没有结点走下去
p = trie[p][u]; //寻找与x的第i位相同的进制，异或结果为0
}
}
sum += cnt[p]; //加上走到最后的结点数
return sum;
}
};
- 动态开点
class Trie {
Trie[] trie = new Trie[2];
int cnt;
}
class Solution {
Trie root;
public int countPairs(int[] nums, int low, int high) {
return get(nums, high) - get(nums, low - 1);
}
int get(int[] nums, int high) {
root = new Trie();
int ans = 0;
for (int i = 0; i < nums.length; i++) {
ans += query(nums[i], high);
add(nums[i]);
}
return ans;
}
void add(int x) {
Trie p = root;
for (int i = 14; i >= 0; i--) {
int u = (x >> i) & 1;
if (p.trie[u] == null) p.trie[u] = new Trie();
p = p.trie[u]; //移动到下一个结点
p.cnt++; // 个数增加，p.cnt代表p结点出现的次数
}
}
int query(int x, int high) {
int sum = 0;
Trie p = root;
for (int i = 14; i >= 0; i--) {
int u = (x >> i) & 1;
if (((high >> i) & 1) == 1) { //high当前i位为1, 那么x与以前数当前i位的异或可以位1或者0
if (p.trie[u] != null) sum += p.trie[u].cnt;//加上与x异或后当前i位为0的数量
if (p.trie[u ^ 1] == null) return sum; //没有结点可以继续走下去，直接返回
p = p.trie[u ^ 1]; //继续往异或的结点走下去
} else { //high当前i位为0, x与以前数异或的第i为必须为0
if (p.trie[u] == null) return sum; //没有结点走下去
p = p.trie[u]; //寻找与x的第i位相同的进制，异或结果为0
}
}
sum += p.cnt; //加上走到最后的结点数
return sum;
}
}
