写在前面
Hello,各位盆友们,我是黄小黄。关于前一段时间为什么拖更这件事,这里给大家说一句抱歉。笔者前段时间忙于ddl和一些比赛相关的事件,当然还有些隐藏任务,所以博文更新就放缓了。

这里还需要做一下对以后博文布局的声明:笔者会尽量减少推广类的内容,着重文章质量的本身,并且由于数据结构非常需要读者自己独立思考,将思考的实现过程内化,并外现成对应的代码,是不能逾越的思考过程。为了避免文章冗余度过高,因此,在分步阐述的时候,这里只展现伪代码或者以文字和图片的形式阐述思路(对于数据结构来说,解法可能不唯一,也欢迎大家与小黄一起交流!),每部分内容结束附上参考代码。最后,感谢这半年来,大家对小黄的支持!
话不多说,今天,我们重新回顾一下,之前所讲到的数据结构(栈、队列、单双链表),并尝试使用一种新的存储形式来组织数据(链式存储栈和队列) 算是对之前学习的一次巩固和升华?

文章目录
- 写在前面
- 1 栈和队列回顾
- 2 双向链表实现栈
- 2.1 思路点拨
- 2.2 参考代码及测试
- 2.3 单向链表实现栈
- 3 双向链表实现队列
- 3.1 思路点拨
- 3.2 参考代码及测试
- 4 单链表实现队列
- 4.1 思路点拨
- 4.2 参考代码及测试
- 写在最后
1 栈和队列回顾
何为栈?何为队列?
用一句话来概括:所谓栈与队列,均是受限制的线性表。对于栈,其有着先进后出的特性,对于队列,其特性就是先进先出。
举个大白栗子:1、2、3、4、5依次入栈或者入队,对于栈,其出栈顺序就是5、4、3、2、1,对于队列,则是1、2、3、4、5。
不知道小伙伴有没有发现,正因为,栈和队列是被限制的线性表,所以,反而相较正常的线性表缺失了些功能?比如:任意位置插入,任意位置删除等等… …
咱也不装了,这不有手就行,更简单了嘛!
来,咱们看一下Java中的集合类,其体系图如下:
LinkedList实现了List接口,但是在其之前还有个叫Deque的东西。而LinkedList也实现了Deque这一接口。

所谓Deque,即double ended queue,是一种双端队列。该队列既可以从队头入队出队,也可以从队尾入队出队。也正是由于这一特性,Deque也常常用来代替Stack。
而其实现子类LinkedList我们就很熟悉了,该类中封装了众多方法。其底层就是我们熟悉的双向链表的结构。同时,在其中,也使用了last指针维护链表的最后一个元素。正因为如此,LinkedList可以实现从头往后,从后往前的两种遍历方式。不仅如此,你也可以在 O(1) 的时间内,做到从头插入、从头删除、从尾插入、从尾删除(成对使用,这就很nice了,既可以当作队列,也可以当作栈,还可以当作普通的线性表使用!)。
回顾了这么多,我们今天主要聊的就是如何使用单双链表实现栈和队列,这里有一个大前提,注意了!!!
由于我们之前使用顺序表去维护这两个数据结构时,其入栈、出栈;入队、出队的时间复杂度都是 O(1),因此,我们使用单双链表去模拟时,也必须满足时间复杂度为常数时间!
学习,就是个由易到难,由入门到入土的… … …呃呃,到精通的过程。我们先尝试使用最简单的双向链表来实现栈和队列。
为什么说简单呢?因为LinkedList双向链表维护了一个last,始终指向最后一个节点,因此,无论是头插、头删,还是尾插、尾删,都可以做到时间复杂度为O(1)的情况下实现。

2 双向链表实现栈
2.1 思路点拨
由于双向链表的特性,且用 last 维护了最后一个节点。对于栈的实现可以采用两种方式:
- 尾插法+尾删法
- 头插法+头删法
这里举例为:头插法和头删法的方式,其示意图如下:
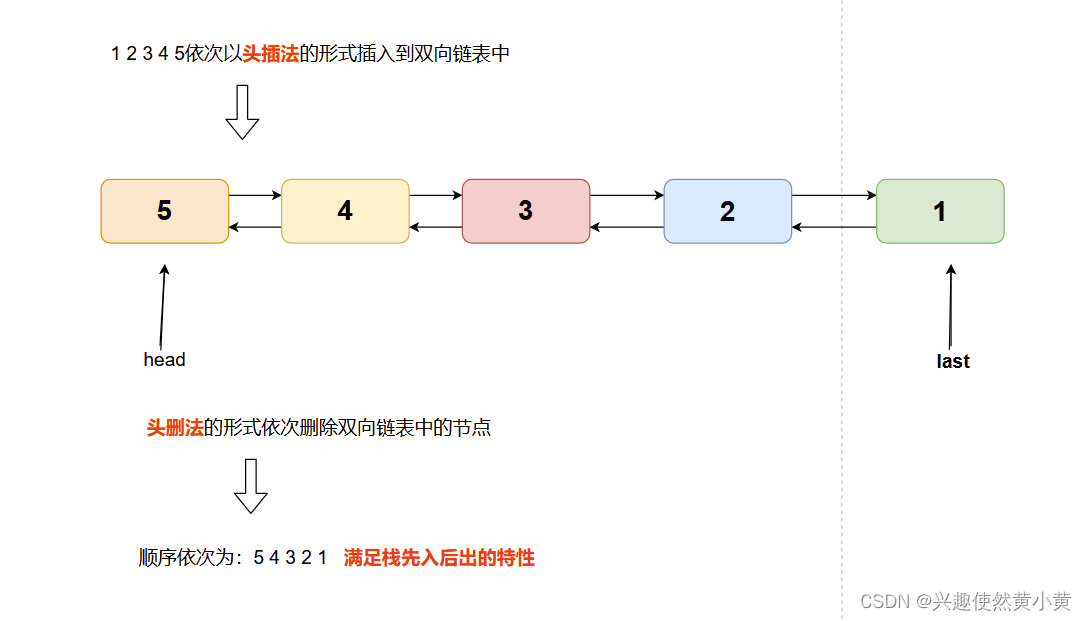
无论是头插法还是头删法,其时间复杂度均为O(1)
2.2 参考代码及测试
/**
* @author 兴趣使然黄小黄
* @version 1.0
* 双向链表实现栈
*/
@SuppressWarnings({"all"})
public class LinkedStack {
private Node head; // 头指针
private Node last; // 始终指向链表的最后一个节点
class Node{
public int data;
public Node pre; // 指向前一个节点
public Node next; // 指向后面一个节点
public Node(int data){
this.data = data;
}
}
public void push(int data){
addFirst(data);
}
public int pop(){
return removeFirst();
}
public int peek(){
return head == null ? null : head.data; // 如果为head为空会报空指针异常 也可以自己处理 或者打印信息
}
//头插法
public void addFirst(int data){
Node newNode = new Node(data);
// 如果head为空,即是第一个节点
if (head == null){
head = newNode;
last = newNode;
return;
}
// 正常的头插法
newNode.next = head;
head.pre = newNode;
head = newNode;
}
// 头删法
public int removeFirst(){
// 如果为空
if (head == null){
throw new RuntimeException("当前为空,无法出栈");
}
// 如果仅剩下一个节点
if (head.next == null){
int val = head.data;
head = null;
last = null;
return val;
}
// 头部删除
int val = head.data;
head = head.next;
return val;
}
//得到栈的长度
public int size(){
int len = 0;
Node cur = head;
while (cur != null){
len++;
cur = cur.next;
}
return len;
}
// 清空栈
public void clear(){
Node cur = head;
while (cur != null){
Node curNext = cur.next;
cur.pre = null;
cur.next = null;
cur = curNext;
}
head = null;
last = null;
}
}
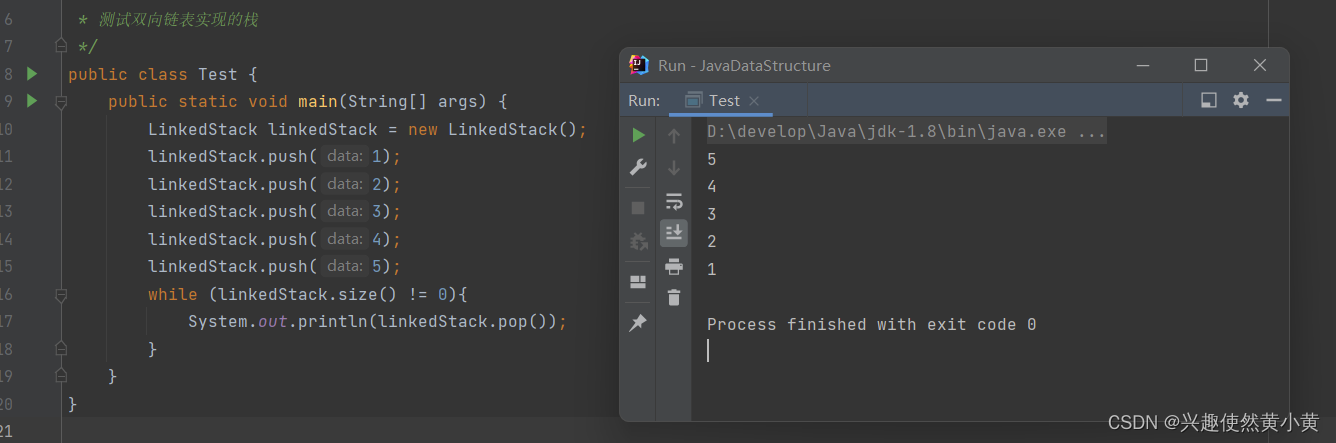
2.3 单向链表实现栈
参考双向链表实现栈采用头插法和头删法分别实现入栈和出栈操作,可以看出来,压根就没有使用到维护的last指针。 所以,对于单链表来说,头插法和头删法时间复杂度也是O(1),因此,很容易就能使用这种方式通过单链表的方式,实现栈。
但是需要特别注意,采用尾插和尾删的方法是不行的!对于单链表来说,由于没有维护 last 指针,并且每次进行尾插的时候都需要遍历到 last 处。
对于尾删操作,每次都需要遍历到last的前一位置,才能实现删除操作(单链表无法实现自身删除)。
对于单链表来说,尾插和尾删的时间复杂度均为O(n)。

3 双向链表实现队列
3.1 思路点拨
同理,对于使用双向链表实现队列,可以考虑以下两种方式:
- 采用头插法+尾删法;
- 采用头删法+尾插法;
这里我们以 头插法+尾删法 为例,实现双向链表模拟队列,示意图如下:
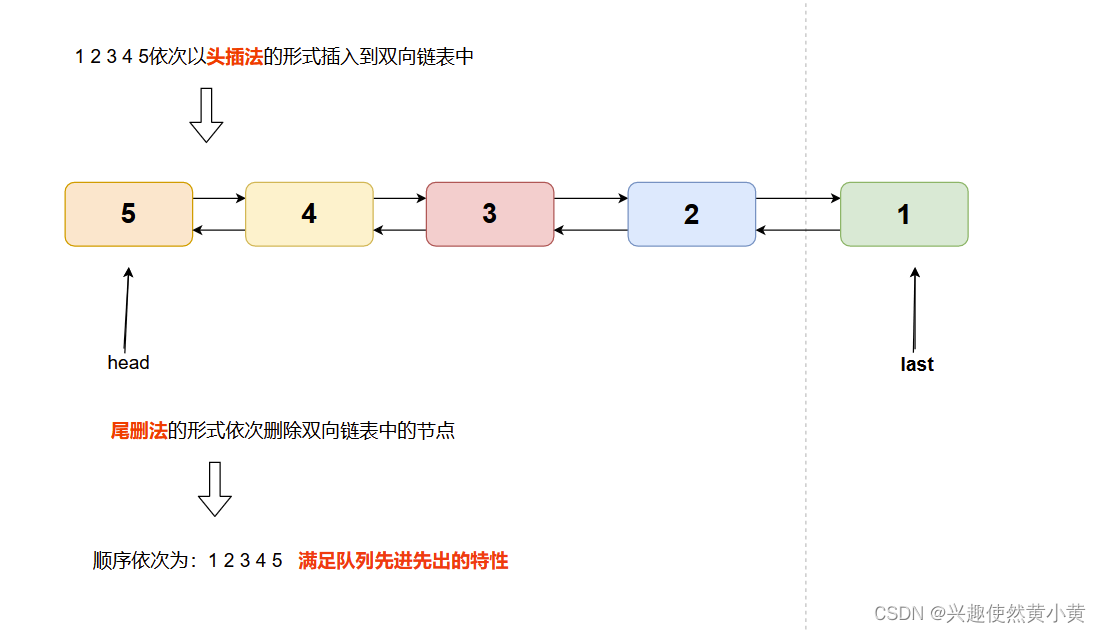
由于双向链表在删除时,不需要知道其邻前节点的位置,可以实现自身删除。所以,对于双向链表实现队列来说,无论是头插法还是尾删,时间复杂度均为O(1)
3.2 参考代码及测试
/**
* @author 兴趣使然黄小黄
* @version 1.0
* 使用双向链表模拟队列
* 采用头插法 + 尾删法的方式
*/
@SuppressWarnings({"all"})
public class LinkedQueue {
private Node head; // 头指针
private Node last; // 始终指向链表的最后一个节点
class Node{
public int data;
public Node pre; // 指向前一个节点
public Node next; // 指向后面一个节点
public Node(int data){
this.data = data;
}
}
// 入队
public void offer(int data){
addFirst(data);
}
// 出队
public int poll(){
return removeLast();
}
// 获取队头元素
public int peek(){
return last == null ? null : last.data; // 如果为head为空会报空指针异常 也可以自己处理 或者打印信息
}
//头插法
public void addFirst(int data){
Node newNode = new Node(data);
// 如果head为空,即是第一个节点
if (head == null){
head = newNode;
last = newNode;
return;
}
// 正常的头插法
newNode.next = head;
head.pre = newNode;
head = newNode;
}
// 头删法
public int removeLast(){
// 如果为空
if (head == null){
throw new RuntimeException("当前为空,无法出队");
}
// 如果仅剩下一个节点
if (last == head){
int val = last.data;
head = null;
last = null;
return val;
}
// 尾部删除
int val = last.data;
last = last.pre;
return val;
}
//得到队列的长度
public int size(){
int len = 0;
Node cur = head;
while (cur != null){
len++;
cur = cur.next;
}
return len;
}
// 清空队列
public void clear(){
Node cur = head;
while (cur != null){
Node curNext = cur.next;
cur.pre = null;
cur.next = null;
cur = curNext;
}
head = null;
last = null;
}
}
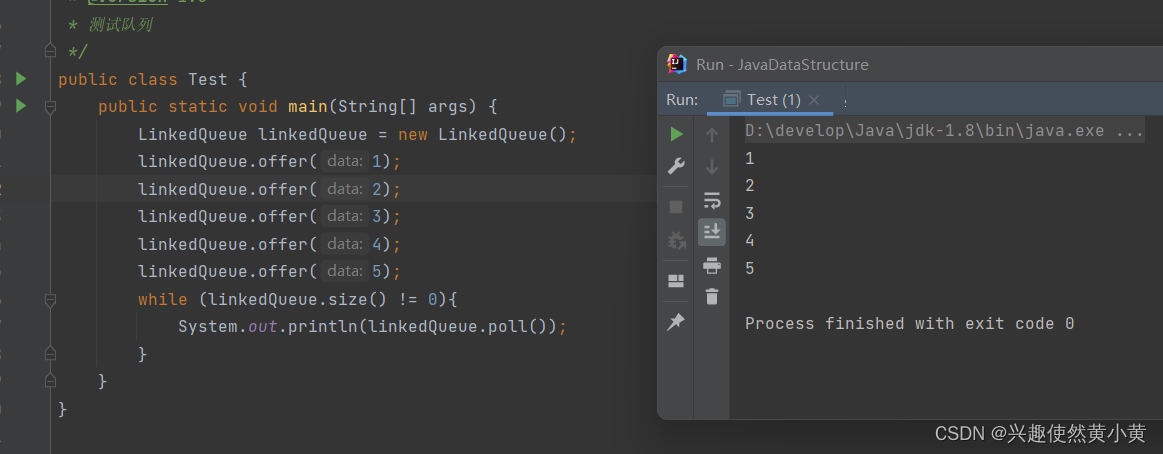
4 单链表实现队列
4.1 思路点拨
思考一个问题
我们可以尝试双向链表类似的方式套用到单链表上,以实现队列吗?
照猫画虎,单链表我们也维护一个指针last,让其始终指向最后一个节点,我们来分析以下时间复杂度:
- 对于 头插法和头删法, 由于头不存在紧邻前节点,因此,时间复杂度都为 O(1);
- 对于尾插法,由于维护了一个 last 始终指向最后一个节点,所以,在尾插的时候,不需要再遍历,典型的空间换时间,因此时间复杂度为O(1);
- 对于尾删法,由于是单向链表,所以在删除的时候,始终需要知道要删除节点的前一个节点,也就是,逃离不了遍历的命运。而,last随着元素个数的减少,还需要更新尾节点的位置,就更没办法更新了。显然,时间复杂度是O(n)。
显然,单链表具有局限性, 我们不能采用像双向链表一样,采用 头插 + 尾删 的方式模拟队列(限定了时间复杂度为O(1)),因此,我们考虑使用另一种方式,头删 + 尾插! 示意图如下:
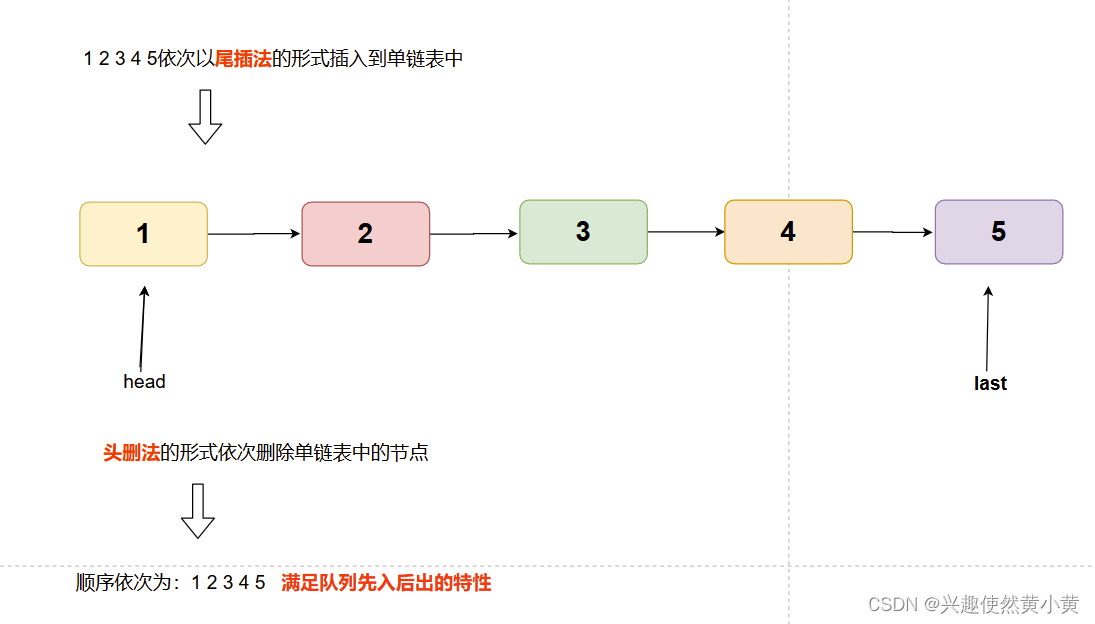
对于头删和尾插,时间复杂度均为O(1)
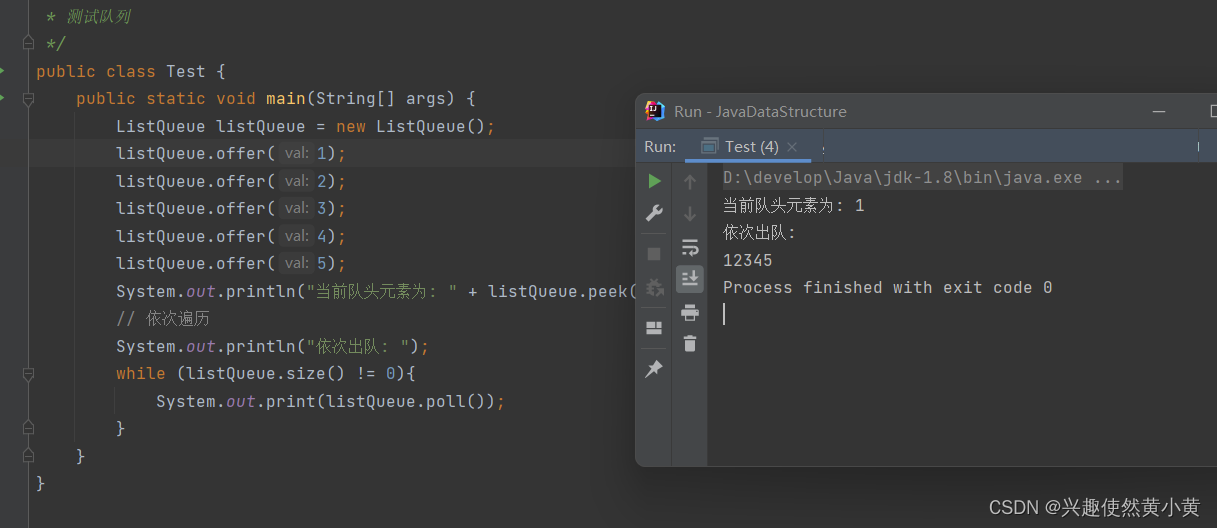
4.2 参考代码及测试
/**
* @author 兴趣使然黄小黄
* @version 1.0
* 单链表实现队列
* 尾插 + 头删
*/
@SuppressWarnings({"all"})
public class ListQueue {
public Node head; // 指向链表的头
public Node last; // 指向链表的尾
class Node{
public int val; // 存储的数据
public Node next; // 存储下一个节点的地址
public Node(int val) {
this.val = val;
}
}
// 入队列
public void offer(int val){
addLast(val);
}
// 出队列
public int poll(){
return removeFirst();
}
// 查看队头元素
public int peek(){
if (head == null){
throw new RuntimeException("当前队列为空!");
}
return head.val;
}
// 头删法
public int removeFirst(){
// 判空
if (head == null){
throw new RuntimeException("当前队列为空!");
}
// 考虑只剩下一个节点
if (head.next == null){
int val = head.val;
head = null;
last = null;
return val;
}
// 头部删除
int val = head.val;
head = head.next;
return val;
}
// 尾插法
public void addLast(int val){
Node newNode = new Node(val);
if (head == null){
// 链表为空
head = newNode;
last = newNode;
return;
}
// 尾插
last.next = newNode;
last = last.next;
}
// 返回队列的长度
public int size(){
int count = 0;
Node cur = head;
while (cur != null){
count++;
cur = cur.next;
}
return count;
}
}
写在最后
本文被 Java数据结构 收录点击订阅专栏 , 持续更新中。
创作不易,如果你有任何问题,欢迎私信,感谢您的支持!