高、低成本MEMS惯导系统姿态、位置、速度更新算法的对比
- 一、高成本MEMS惯导系统姿态、位置、速度更新算法
- 1、速度更新
- 2、位置更新
- 3、姿态更新
- 4、程序仿真及实验结果
- 4.1 主函数
- 4.2 子函数
- 4.3 实验结果
- 一、低成本MEMS惯导系统姿态、位置、速度更新算法
- 1、速度更新
- 2、位置更新
- 3、姿态更新
- 4、程序仿真及实验结果
- 4.1 主函数
- 4.2 子函数
- 4.3 实验结果
- 1. 不考虑地球自转的影响
- 2. 考虑地球自转的影响
- 5. 程序代码及数据下载地址
一、高成本MEMS惯导系统姿态、位置、速度更新算法
1、速度更新
wie= 7.2921151467e-5; %自传角速度 wgs-84 model
eth.sl = sin(pos(1)); eth.cl = cos(pos(1)); eth.tl = eth.sl/eth.cl; % eth.sl -- sinL;eth.cl -- cosL;eth.tl -- tanL;
eth.RMh = Re*(1-e2)/sq/sq2+pos(3); % 子午圈主曲率半径+飞行高度 (3.1.23)
eth.RNh = Re/sq2+pos(3); eth.clRNh = eth.cl*eth.RNh; % 卯酉圈主曲率半径+飞行高度 (3.1.24)
eth.wnie = wie*[0; eth.cl; eth.sl]; % 地球自转角速度三个分量值x y z
eth.wnen = [-vn(2)/eth.RMh; vn(1)/eth.RNh; vn(1)/eth.RNh*eth.tl]; % 载体运动的角速度分量,设定东“+”西“-”。 (3.1.24)
eth.wnin = eth.wnie + eth.wnen; % 载体相对惯性系的角速度; eth.wnie -- 地球自转引起的导航系旋转 eth.wnen -- 惯导系统在地球表面附近移动因地球表面弯曲引起的n系旋转;
[phim, dvbm] = cnscl(wm, vm); % 圆锥误差/划船误差补偿;phim -- 补偿后旋转矢量;dvbm -- 补偿后速度增量dvbm = (vmm+0.5*cross(wmm,vmm)+scullm)';
eth.gcc = eth.gn - cross(eth.wnien,vn); % 考虑重力/哥氏力/向心力
nn = 2; ts = 0.1; nts = nn*ts; % nn -- 子样数;ts -- 采样时间间隔;nts -- 采样周期
% 速度更新
vn1 = vn + rv2m(-eth.wnin*nts/2)*qmulv(qnb,dvbm) + eth.gcc*nts; % rv2m -- 等效旋转矢量转换为方向余弦;qmulv -- 四元数乘矢量,即三维矢量的四元数坐标变换(2.4-26)
v
m
n
(
m
)
=
v
m
−
1
n
(
m
−
1
)
+
Δ
v
s
f
(
m
)
n
+
Δ
v
c
o
r
/
g
(
m
)
n
{\bf{v}}_m^{n(m)} = {\bf{v}}_{m - 1}^{n(m - 1)} + \Delta {\bf{v}}_{{\rm{sf}}(m)}^n + \Delta {\bf{v}}_{{\rm{cor/g}}(m)}^n
vmn(m)=vm−1n(m−1)+Δvsf(m)n+Δvcor/g(m)n
Δ
v
s
f
(
m
)
n
≈
[
I
−
T
2
(
ω
i
n
(
m
−
1
/
2
)
n
×
)
]
C
b
(
m
−
1
)
n
(
m
−
1
)
(
Δ
v
m
+
Δ
v
r
o
t
(
m
)
b
(
m
−
1
)
+
Δ
v
s
c
u
l
(
m
)
b
(
m
−
1
)
)
\Delta {\bf{v}}_{{\rm{sf}}(m)}^n \approx \left[ {{\bf{I}} - \frac{T}{2}({\bf{\omega }}_{in(m - 1/2)}^n \times )} \right]{\bf{C}}_{b(m - 1)}^{n(m - 1)}(\Delta {{\bf{v}}_m} + \Delta {\bf{v}}_{{\rm{rot}}(m)}^{b(m - 1)}{\rm{ + }}\Delta {\bf{v}}_{{\rm{scul}}(m)}^{b(m - 1)})
Δvsf(m)n≈[I−2T(ωin(m−1/2)n×)]Cb(m−1)n(m−1)(Δvm+Δvrot(m)b(m−1)+Δvscul(m)b(m−1))
Δ v c o r / g ( m ) n ≈ { − [ 2 ω i e ( m − 1 / 2 ) n + ω e n ( m − 1 / 2 ) n ] × v m − 1 / 2 n + g m − 1 / 2 n } T \Delta {\bf{v}}_{{\rm{cor/g}}(m)}^n \approx \left\{ { - \left[ {2{\bf{\omega }}_{ie(m - 1/2)}^n + {\bf{\omega }}_{en(m - 1/2)}^n} \right] \times {\bf{v}}_{m - 1/2}^n + {\bf{g}}_{m - 1/2}^n} \right\}T Δvcor/g(m)n≈{−[2ωie(m−1/2)n+ωen(m−1/2)n]×vm−1/2n+gm−1/2n}T
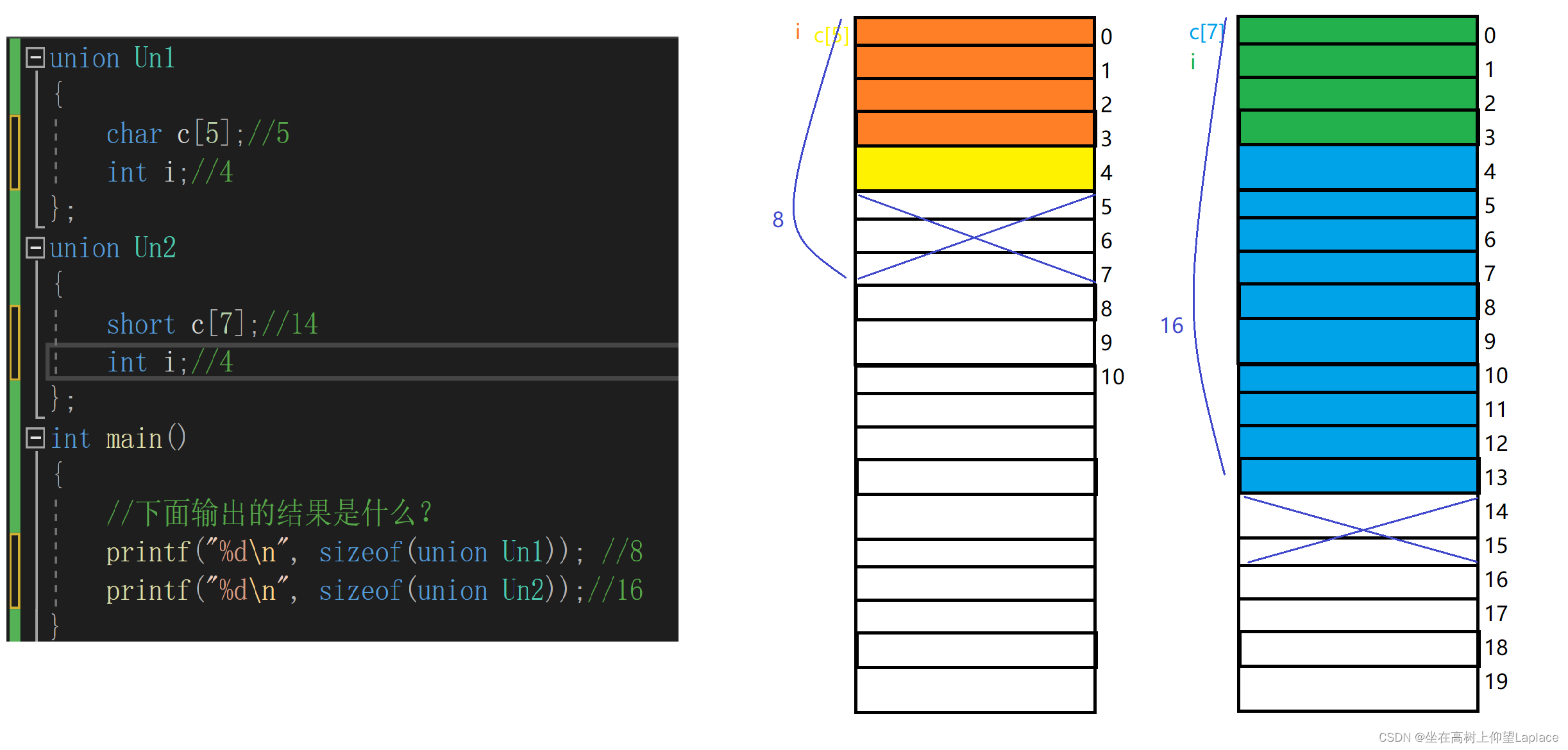
| 符号 | 含义 / 程序中表现为 |
|---|---|
| Δ v s f ( m ) n \Delta {\bf{v}}_{{\rm{sf}}(m)}^n Δvsf(m)n | 导航系比力速度增量 |
| Δ v c o r / g ( m ) n \Delta {\bf{v}}_{{\rm{cor/g}}(m)}^n Δvcor/g(m)n | 有害加速度的速度增量(4.1-27) |
| Δ v r o t ( m ) b ( m − 1 ) \Delta {\bf{v}}_{{\rm{rot}}(m)}^{b(m - 1)} Δvrot(m)b(m−1) | 速度的旋转误差补偿量 |
| Δ v s c u l ( m ) b ( m − 1 ) \Delta {\bf{v}}_{{\rm{scul}}(m)}^{b(m - 1)} Δvscul(m)b(m−1) | 二子样速度划桨误差补偿量 |
| ( Δ v m + Δ v r o t ( m ) b ( m − 1 ) + Δ v s c u l ( m ) b ( m − 1 ) ) (\Delta {{\bf{v}}_m} + \Delta {\bf{v}}_{{\rm{rot}}(m)}^{b(m - 1)}{\rm{ + }}\Delta {\bf{v}}_{{\rm{scul}}(m)}^{b(m - 1)}) (Δvm+Δvrot(m)b(m−1)+Δvscul(m)b(m−1)) | dvbm – 补偿后速度增量dvbm = (vmm+0.5*cross(wmm,vmm)+scullm)'; |
| [ I − T 2 ( ω i n ( m − 1 / 2 ) n × ) ] \left[ {{\bf{I}} - \frac{T}{2}({\bf{\omega }}_{in(m - 1/2)}^n \times )} \right] [I−2T(ωin(m−1/2)n×)] | rv2m(-eth.wnin*nts/2) |
| { − [ 2 ω i e ( m − 1 / 2 ) n + ω e n ( m − 1 / 2 ) n ] × v m − 1 / 2 n + g m − 1 / 2 n } \left\{ { - \left[ {2{\bf{\omega }}_{ie(m - 1/2)}^n + {\bf{\omega }}_{en(m - 1/2)}^n} \right] \times {\bf{v}}_{m - 1/2}^n + {\bf{g}}_{m - 1/2}^n} \right\} {−[2ωie(m−1/2)n+ωen(m−1/2)n]×vm−1/2n+gm−1/2n} | eth.gcc = eth.gn - cross(eth.wnien,vn); % 考虑重力/哥氏力/向心力 |
2、位置更新
eth.RMh = Re*(1-e2)/sq/sq2+pos(3); % 子午圈主曲率半径+飞行高度 (3.1.23)
eth.RNh = Re/sq2+pos(3); eth.clRNh = eth.cl*eth.RNh; % 卯酉圈主曲率半径+飞行高度 (3.1.24)
nn = 2; ts = 0.1; nts = nn*ts; % nn -- 子样数;ts -- 采样时间间隔;nts -- 采样周期
% 位置更新
vn = (vn+vn1)/2;
pos = pos + [vn(2)/eth.RMh;vn(1)/eth.clRNh;vn(3)]*nts;
vn = vn1;
p m = p m − 1 + M p v ( m − 1 / 2 ) ( v m − 1 n ( m − 1 ) + v m n ( m ) ) T 2 {{\bf{p}}_m} = {{\bf{p}}_{m - 1}} + {{\bf{M}}_{pv(m - 1/2)}}({\bf{v}}_{m - 1}^{n(m - 1)} + {\bf{v}}_m^{n(m)})\frac{T}{2} pm=pm−1+Mpv(m−1/2)(vm−1n(m−1)+vmn(m))2T

3、姿态更新
姿态更新求解方法是,先使用陀螺角增量的多子样采样计算等效旋转矢量,补偿转动不可交换误差,再使用等效旋转矢量计算姿态更新四元数。
选取“东–北–天(E–N–U)”地理坐标系作为捷联惯导系统的导航参考坐标系,后面记为n系,则以 系作为参考系的姿态微分方程为
eth.wnin = eth.wnie + eth.wnen; % 载体相对惯性系的角速度
[phim, dvbm] = cnscl(wm, vm); % 圆锥误差/划船误差补偿;phim -- 圆锥补偿后旋转矢量;dvbm -- 划桨补偿后速度增量dvbm = (vmm+0.5*cross(wmm,vmm)+scullm)';
% 姿态更新
qnb = qmul(rv2q(-eth.wnin*nts), qmul(qnb, rv2q(phim)));
qnb = qnormlz(qnb);
ω
i
n
n
{\bf{\omega }}_{in}^n
ωinn表示n系相对于i系的旋转,它包含两部分:地球自转引起的导航系旋转,以及惯导系统在地球表面附近移动因地球表面弯曲引起的n系旋转:
ω
i
n
n
=
ω
i
e
n
+
ω
e
n
n
{\bf{\omega }}_{in}^n = {\bf{\omega }}_{ie}^n + {\bf{\omega }}_{en}^n
ωinn=ωien+ωenn
C
b
(
m
)
b
(
m
−
1
)
{\bf{C}}_{b(m)}^{b(m - 1)}
Cb(m)b(m−1)矩阵表示以i系作为参考基准,b系从m-1时刻到m时刻的旋转变化,
C
b
(
m
)
b
(
m
−
1
)
{\bf{C}}_{b(m)}^{b(m - 1)}
Cb(m)b(m−1)可由陀螺角速度
ω
i
b
b
{\bf{\omega }}_{ib}^b
ωibb确定;
C
n
(
m
−
1
)
n
(
m
)
{\bf{C}}_{n(m - 1)}^{n(m)}
Cn(m−1)n(m)表示以i系作为参考基准,n系从m-1时刻到m时刻的旋转变化,
C
n
(
m
−
1
)
n
(
m
)
{\bf{C}}_{n(m - 1)}^{n(m)}
Cn(m−1)n(m)可由计算角速度
−
ω
i
n
n
- {\bf{\omega }}_{in}^n
−ωinn确定。
C
b
(
m
)
n
(
m
)
=
C
n
(
m
−
1
)
n
(
m
)
C
i
n
(
m
−
1
)
C
b
(
m
−
1
)
i
C
b
(
m
)
b
(
m
−
1
)
=
C
n
(
m
−
1
)
n
(
m
)
C
b
(
m
−
1
)
n
(
m
−
1
)
C
b
(
m
)
b
(
m
−
1
)
{\bf{C}}_{b(m)}^{n(m)} = {\bf{C}}_{n(m - 1)}^{n(m)}{\bf{C}}_i^{n(m - 1)}{\bf{C}}_{b(m - 1)}^i{\bf{C}}_{b(m)}^{b(m - 1)} = {\bf{C}}_{n(m - 1)}^{n(m)}{\bf{C}}_{b(m - 1)}^{n(m - 1)}{\bf{C}}_{b(m)}^{b(m - 1)}
Cb(m)n(m)=Cn(m−1)n(m)Cin(m−1)Cb(m−1)iCb(m)b(m−1)=Cn(m−1)n(m)Cb(m−1)n(m−1)Cb(m)b(m−1)
Q
b
(
m
)
n
(
m
)
=
Q
n
(
m
−
1
)
n
(
m
)
Q
i
n
(
m
−
1
)
Q
b
(
m
−
1
)
i
Q
b
(
m
)
b
(
m
−
1
)
=
Q
n
(
m
−
1
)
n
(
m
)
Q
b
(
m
−
1
)
n
(
m
−
1
)
Q
b
(
m
)
b
(
m
−
1
)
{\bf{Q}}_{b(m)}^{n(m)} = {\bf{Q}}_{n(m - 1)}^{n(m)}{\bf{Q}}_i^{n(m - 1)}{\bf{Q}}_{b(m - 1)}^i{\bf{Q}}_{b(m)}^{b(m - 1)} = {\bf{Q}}_{n(m - 1)}^{n(m)}{\bf{Q}}_{b(m - 1)}^{n(m - 1)}{\bf{Q}}_{b(m)}^{b(m - 1)}
Qb(m)n(m)=Qn(m−1)n(m)Qin(m−1)Qb(m−1)iQb(m)b(m−1)=Qn(m−1)n(m)Qb(m−1)n(m−1)Qb(m)b(m−1)
若陀螺在时间段
[
t
m
−
1
,
t
m
]
[{t_{m - 1}},{t_m}]
[tm−1,tm] 内(
T
=
t
m
−
t
m
−
1
T = {t_m} - {t_{m - 1}}
T=tm−tm−1)进行了两次等间隔采样,角增量分别为
Δ
θ
m
1
{\rm{\Delta }}{{\bf{\theta }}_{m1}}
Δθm1和
Δ
θ
m
2
{\rm{\Delta }}{{\bf{\theta }}_{m2}}
Δθm2 ,采用二子样圆锥误差补偿算法,有
C
b
(
m
)
b
(
m
−
1
)
=
M
R
V
(
ϕ
i
b
(
m
)
b
)
{\bf{C}}_{b(m)}^{b(m - 1)} = {{\bf{M}}_{{\rm{RV}}}}({\phi }_{ib(m)}^b)
Cb(m)b(m−1)=MRV(ϕib(m)b)
ϕ
i
b
(
m
)
b
=
(
Δ
θ
m
1
+
Δ
θ
m
2
)
+
2
3
Δ
θ
m
1
×
Δ
θ
m
2
{\phi }_{ib(m)}^b = ({\rm{\Delta }}{{\bf{\theta }}_{m1}} + {\rm{\Delta }}{{\bf{\theta }}_{m2}}) + \frac{2}{3}{\rm{\Delta }}{{\bf{\theta }}_{m1}} \times {\rm{\Delta }}{{\bf{\theta }}_{m2}}
ϕib(m)b=(Δθm1+Δθm2)+32Δθm1×Δθm2
由速度和位置引起的
ω
i
n
n
{\bf{\omega }}_{in}^n
ωinn变化很小,即
ω
i
n
n
{\bf{\omega }}_{in}^n
ωinn可视为常值:
C
n
(
m
−
1
)
n
(
m
)
=
(
C
n
(
m
)
n
(
m
−
1
)
)
T
=
M
R
V
T
(
ϕ
i
n
(
m
)
n
)
≈
M
R
V
T
(
T
ω
i
n
(
m
)
n
)
{\bf{C}}_{n(m - 1)}^{n(m)} = {({\bf{C}}_{n(m)}^{n(m - 1)})^{\rm{T}}} = {\bf{M}}_{{\rm{RV}}}^{\rm{T}}({\phi }_{in{\rm{(}}m)}^n) \approx {\bf{M}}_{RV}^{\rm{T}}(T{\bf{\omega }}_{in(m)}^n)
Cn(m−1)n(m)=(Cn(m)n(m−1))T=MRVT(ϕin(m)n)≈MRVT(Tωin(m)n)
=
I
+
sin
ϕ
ϕ
(
ϕ
×
)
+
1
−
cos
ϕ
ϕ
2
(
ϕ
×
)
2
= {\bf{I}} + \frac{{\sin \phi }}{\phi }(\boldsymbol{\phi } \times ) + \frac{{1 - \cos \phi }}{{{\phi ^2}}}{(\boldsymbol{\phi } \times )^2}
=I+ϕsinϕ(ϕ×)+ϕ21−cosϕ(ϕ×)2
| 符号 | 含义 / 程序中表现为 |
|---|---|
| C n ( m − 1 ) n ( m ) {\bf{C}}_{n(m - 1)}^{n(m)} Cn(m−1)n(m) | rv2q(-eth.wnin*nts) |
| C b ( m ) b ( m − 1 ) {\bf{C}}_{b(m)}^{b(m - 1)} Cb(m)b(m−1) | rv2q(phim);phim = (wmm+dphim)';dphim = cross(csw,wm(n,:)); % 圆锥补偿量 |
4、程序仿真及实验结果
4.1 主函数
clear
clc
format long
gvar; %加载全局变量
nn=1; %子样数,采用二样子圆锥误差补偿算法
ts=0.01; %单个采样间隔的采样时间长度
nts=nn*ts; %采样周期,在nts时间内进行两次采样,每次采样 0.1秒
%输入姿态角向量att含三个分量,依次为俯仰角θ(Theta),横滚角γ(Gama),航向角ψ(Fai)
att = [0;0;90]*arcdeg; vn = [0;0;0]; pos = [[34;108]*arcdeg;100];
% att=[-1.42701;0.569073;-176.015]*arcdeg;
% vn=[0;0;0]; %初始化速度
% %初始位置 纬度(B)34.8222007度 ,经度(L)113.4845389度 ,高度(h)87.2566m B L H相当于大地坐标系的纬度、经度、高度
% pos=[34.8222007*arcdeg;113.4845389*arcdeg;87.2566];
qnb=a2qua(att);% 姿态、速度和位置初始化 ;姿态角转换为四元数 b->n
%仿真静态IMU数据
% eth=earth(pos,vn); %地球导航参数参数计算
% %qconj 四元数共轭,地球自转角速度由 导航系换算到机体系,作为机体角速度,并乘时间得到角度增量
% wm=qmulv(qconj(qnb),eth.wnie)*ts;
% %比力由 导航系换算到机体系,作为机体比力,并乘时间得速度增量
% vm=qmulv(qconj(qnb),-eth.gn)*ts;
% wm=repmat(wm',nn,1); %repmat 重复数组副本。转置角速度矢量,并复制到nn行'1'列 相当于二子样
% vm=repmat(vm',nn,1); %转置速度矢量,并复制得到nn行'1'列
%仿真时间
phi=[0.1;0.2;3]*arcmin; %由计算四元数和真实四元数计算失准角误差 phi
qnb=qaddphi(qnb,phi); %四元数加失准角误差 转换为qnb
len=fix(100/ts)-1; %仿真时长,得到fix(1550/ts)个子样 fix(1550/ts)
avp=zeros(len,10); %由零组成的len*10的向量
kk=1;
t=0;
load('imu.mat'); %加载imu数据 avp=[wm, vm, tt(2:end)]; gx(rad) gy gz ax (m/s) ay az time
trj=load ('trj.mat'); %trj=[att, vn, pos]; att(度) vn(米每秒) pos(米)
avp1=zeros(fix(len/2+1),10);
avp1(1,:)=[att;vn;pos;0]';
%记录导航结果[att,vn,pos,t] 共有len个子样,每个采样时间段nn个子样,共len/nn个时间段,循环len/nn步
for k=1:nn:len-1 %k是两次一跳,因为采用的是二子样,36000是6分钟开始解算
t=t+nts; %t表示采样时间段
wm=avp(k,1:3);
vm=avp(k,4:6);
[qnb,vn,pos]=insupdate(qnb,vn,pos,wm,vm,ts);
kk=kk+1;
avp1(kk,:)=[q2att(qnb);vn;pos;t]'; %avp()=[θ γ ψ VE VN VU B L h t]
if mod(t,1)<nts, disp(fix(t));
end %显示进度 disp函数:显示文本或数组
end
%取出avp中只有1s时的数据
x=fix(len/100);
avp0=zeros(x,10);
k1=1;
for i=1:length(avp1)
c=mod(avp1(i,10),1);
d=1-c;
if(c<0.0000000001||d<=0.000001)
avp0(k1,:)=avp1(i,:); %avp1()=[θ γ ψ VE VN VU B L h t*100]
k1=k1+1;
end
end
%姿态
tt=length(avp1);
tf=length(trj.trj);
figure(1);
subplot(211);
plot(1:tt,(avp1(1:tt,1:2)/arcdeg),1:tf,(trj.trj(1:tf,1:2)/arcdeg),'--'); title('俯仰角和横滚角');xlabel('d');ylabel('\theta,\gamma(\circ)');
legend('\it\theta','\it\gamma','\bf\theta','\bf\gamma') ;grid on;
subplot(212);
plot(1:tt,(avp1(1:tt,3)/arcdeg),1:tf,(trj.trj(1:tf,3)/arcdeg),'--'); title('偏航角');xlabel('d');ylabel('\Phi(\circ)');
legend('\it\Phi','\bf\Phi') ;grid on;
figure(2);
subplot(211);
plot(1:tt,(avp1(1:tt,4:5)/arcdeg),1:tf,(trj.trj(1:tf,4:5)/arcdeg),'--'); title('速度');xlabel('d');ylabel('Vel/(m.s^{-1})');
legend('\itv\rm_E','\itv\rm_N','\bfv\rm_E','\bfv\rm_N')
subplot(212);grid on;
plot(1:tt,(avp1(1:tt,6)/arcdeg),1:tf,(trj.trj(1:tf,6)/arcdeg),'--'); title('速度');xlabel('d');ylabel('Vel/(m.s^{-1})');
legend('\itv\rm_U','\bfv\rm_U');grid on;
figure(3);
plot(1:tt,deltapos(avp1(1:tt,7:9)),1:tf,deltapos(trj.trj(1:tf,7:9)),'--'); title('位置');xlabel('d');ylabel('\DeltaPos / m');
legend('\Delta\itL', '\Delta\it\lambda', '\Delta\ith','\Delta\bfL', '\Delta\bf\lambda', '\Delta\bfh');grid on;
4.2 子函数
function [qnb, vn, pos, eth] = insupdate(qnb, vn, pos, wm, vm, ts) % 捷联惯导数值更新算法
nn = size(wm,1); nts = nn*ts;
[phim, dvbm] = cnscl(wm, vm); % 圆锥误差/划船误差补偿;phim -- 补偿后旋转矢量;dvbm -- 补偿后速度增量
eth = earth(pos, vn); % 地球相关参数计算
vn1 = vn + rv2m(-eth.wnin*nts/2)*qmulv(qnb,dvbm) + eth.gcc*nts; % 速度更新
vn = (vn+vn1)/2;
pos = pos + [vn(2)/eth.RMh;vn(1)/eth.clRNh;vn(3)]*nts; vn = vn1; % 位置更新
qnb = qmul(rv2q(-eth.wnin*nts), qmul(qnb, rv2q(phim))); % 姿态更新
qnb = qnormlz(qnb);
function eth = earth(pos, vn) % 地球相关参数计算
global Re ff wie g0
ee = sqrt(2*ff-ff^2); e2 = ee^2; % 第一偏心率
eth.sl = sin(pos(1)); eth.cl = cos(pos(1)); eth.tl = eth.sl/eth.cl; % eth.sl -- sinL;eth.cl -- cosL;eth.tl -- tanL;
eth.sl2 = eth.sl*eth.sl; sl4 = eth.sl2*eth.sl2; % eth.sl2 -- (sinL)^2;sl4 -- (sin2L)^2
sq = 1-e2*eth.sl2; sq2 = sqrt(sq);
eth.RMh = Re*(1-e2)/sq/sq2+pos(3); % 子午圈主曲率半径+飞行高度 (3.1.23)
eth.RNh = Re/sq2+pos(3); eth.clRNh = eth.cl*eth.RNh; % 卯酉圈主曲率半径+飞行高度 (3.1.24)
eth.wnie = wie*[0; eth.cl; eth.sl]; % 地球自转角速度三个分量值x y z
eth.pos = pos; eth.vn = vn; % 载体运行的速度等地球速度,作为已知量
eth.wnen = [-vn(2)/eth.RMh; vn(1)/eth.RNh; vn(1)/eth.RNh*eth.tl]; % 载体运动的角速度分量,设定东“+”西“-”。 (3.1.24)
eth.wnin = eth.wnie + eth.wnen; % 载体相对惯性系的角速度
eth.wnien = eth.wnie + eth.wnin; % 由比力方程推导的公式,2wie+wen
gLh = g0*(1+5.27094e-3*eth.sl2+2.32718e-5*sl4)-3.086e-6*pos(3); % grs80重力模型 (3.2.23) g0=ge;考虑高度不变,不加pos(3)
eth.gn = [0;0;-gLh];
eth.gcc = eth.gn - cross(eth.wnien,vn); % 考虑重力/哥氏力/向心力
% %全局变量(gvar)
% global GM Re ff wie ge gp ug arcdeg arcmin arcsec hur dph dpsh ugpsHz %定义全局变量
% GM=3.986004415e14; %引力
% Re=6.378136998405e6; %赤道长半轴
% wie= 7.2921151467e-5; %自传角速度 wgs-84 model
% ff=1/298.257223563; %扁率
% ee=sqrt(2*ff-ff^2); %扁心率
% e2=ee^2;
% Rp=(1-ff)*Re; %极轴半径
% ge=9.780325333434361; %ge 赤道重力加速度
% gp=9.832184935381024; %gp 极点重力加速度
% g0=9.780325333434361; %重力加速度
% ug=ge*1e-6; %ug 微重力加速度
% arcdeg=pi/180; %弧度=角度×π÷180°
% arcmin=arcdeg/60;
% arcsec=arcmin/60; %angle unit .acdeg为弧度
% hur=3600;
% dph=arcdeg/hur;
% dpsh=arcdeg/sqrt(hur); %hour;deg/hour;deg/sqrt(hour)
% ugpsHz= ug/sqrt(1); %ug/sqrt(Hz)
4.3 实验结果
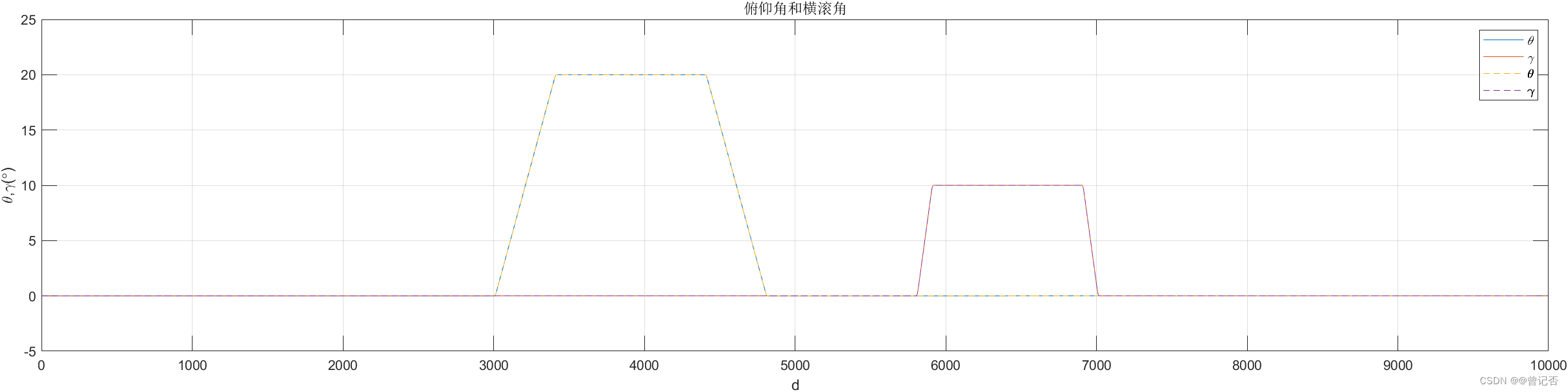
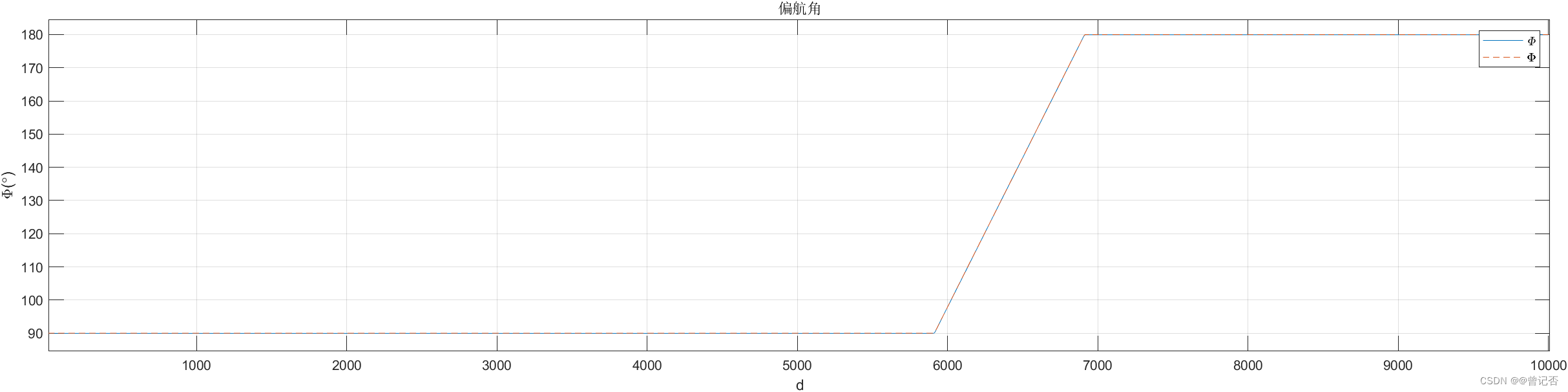
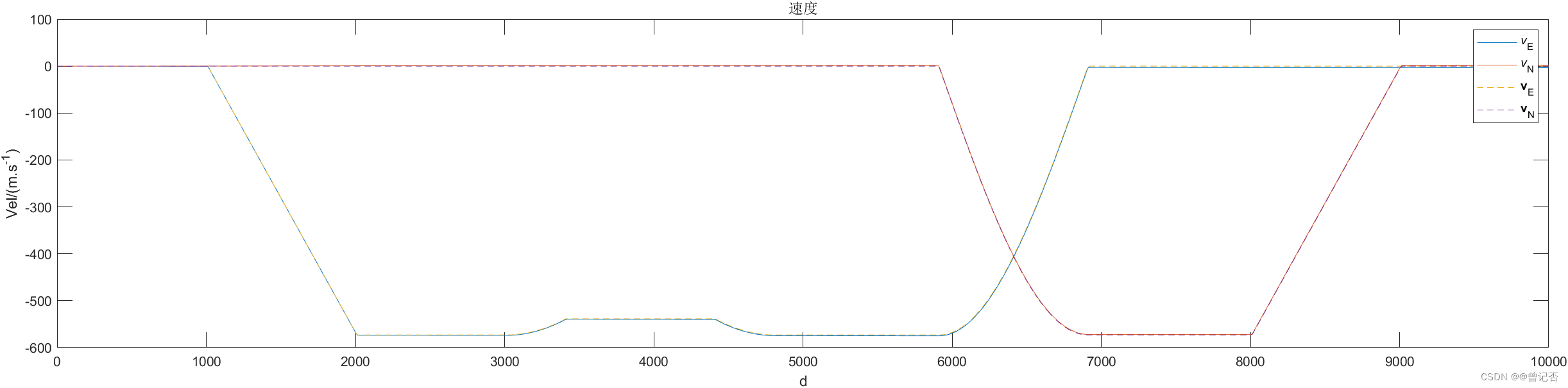
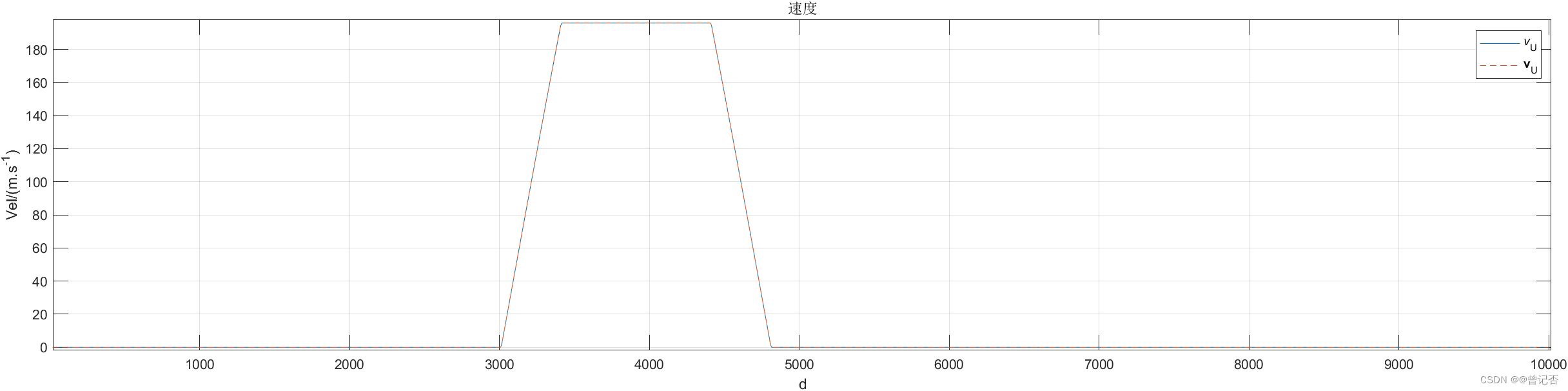
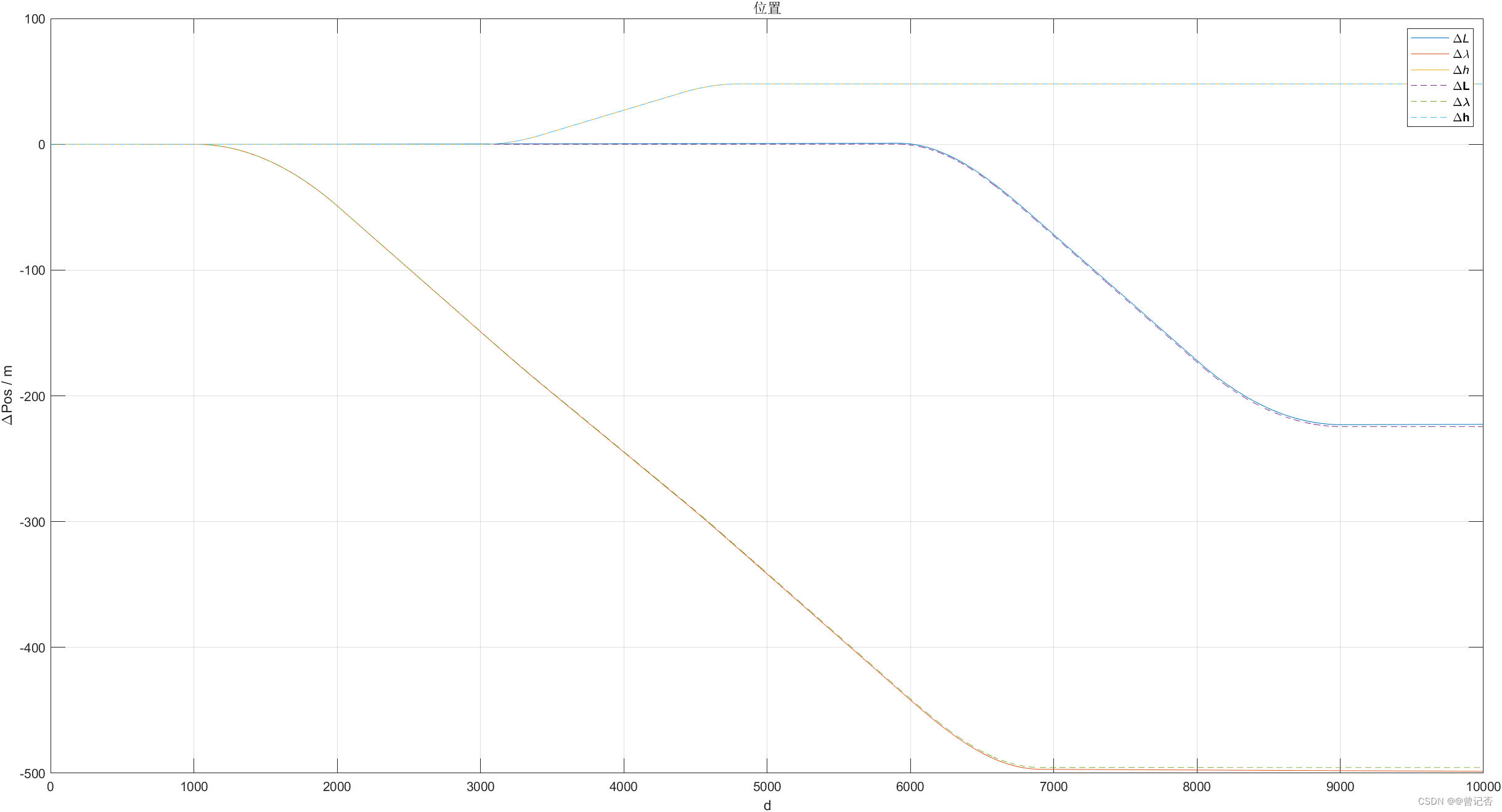
一、低成本MEMS惯导系统姿态、位置、速度更新算法
1、速度更新
忽略地球自转及地球曲率的影响,将速度更新方程简化为:


arcdeg = pi/180;
imu=load ('imu.mat'); //imu数据: avp=[wm, vm, tt(2:end)]; gx(rad) gy gz ax (m/s) ay az time
//imu输出速率信息:
//Tm=2*(imu(2,1)-imu(1,1));
//delta_theta1=imu(1,2:4)*Tm*arcdeg;delta_theta2=imu(2,2:4)*Tm*arcdeg;
//imu输出增量信息:
delta_theta_m=imu.avp(k,1:3);
delta_v_m=imu.avp(k,4:6);
pos = [34*arcdeg; 108*arcdeg; 100]; //位置初始化
//求gn:
g0=9.780325333434361;%单位;m/s^2
sl = sin(pos(1)); % pos(1)=L
sl2 = sl*sl; sl4 = sl2*sl2;
gLh = g0*(1+5.27094e-3*sl2+2.32718e-5*sl4)-3.086e-6*pos(3);
gn = [0;0;-gLh];
//速度更新:
vsf =q2mat(qnb)*(delta_v_m + 1/2*cross(delta_theta_m,delta_v_m))';
vn2 = vn1 + vsf + gn*nts; // %avp2(4:6) = avp1(4:6) + vsf + gn*Tm;
2、位置更新

不考虑单位换算:
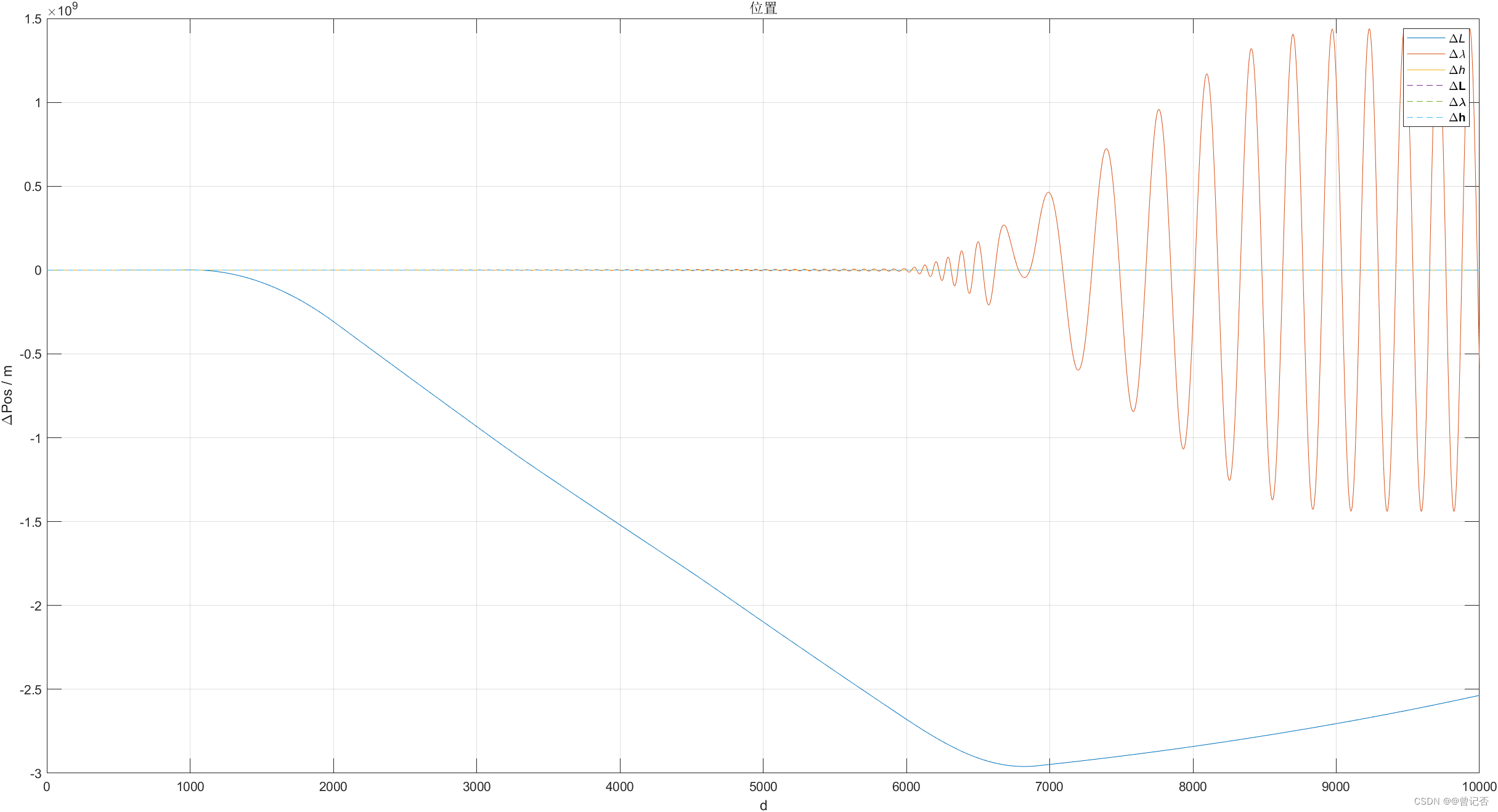
%%%%%%%%1.按书上编写,未做修改,经度会产生剧烈震荡%%%%%%%%%%%%%%%%%
pos = pos+((vn1+vn2)/2)*nts; //avp2(7:9)=avp1(7:9)+(avp1(4:6)+avp2(4:6))*Tm/2;
考虑单位换算,以及对误差进行补偿:
%%%%%%%%2.速度项乘以Mpv(4-1.58)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
vn1 = (vn2+vn1)/2;
pos = pos + [vn1(2)/eth.RMh;vn1(1)/eth.clRNh;vn1(3)]*nts;
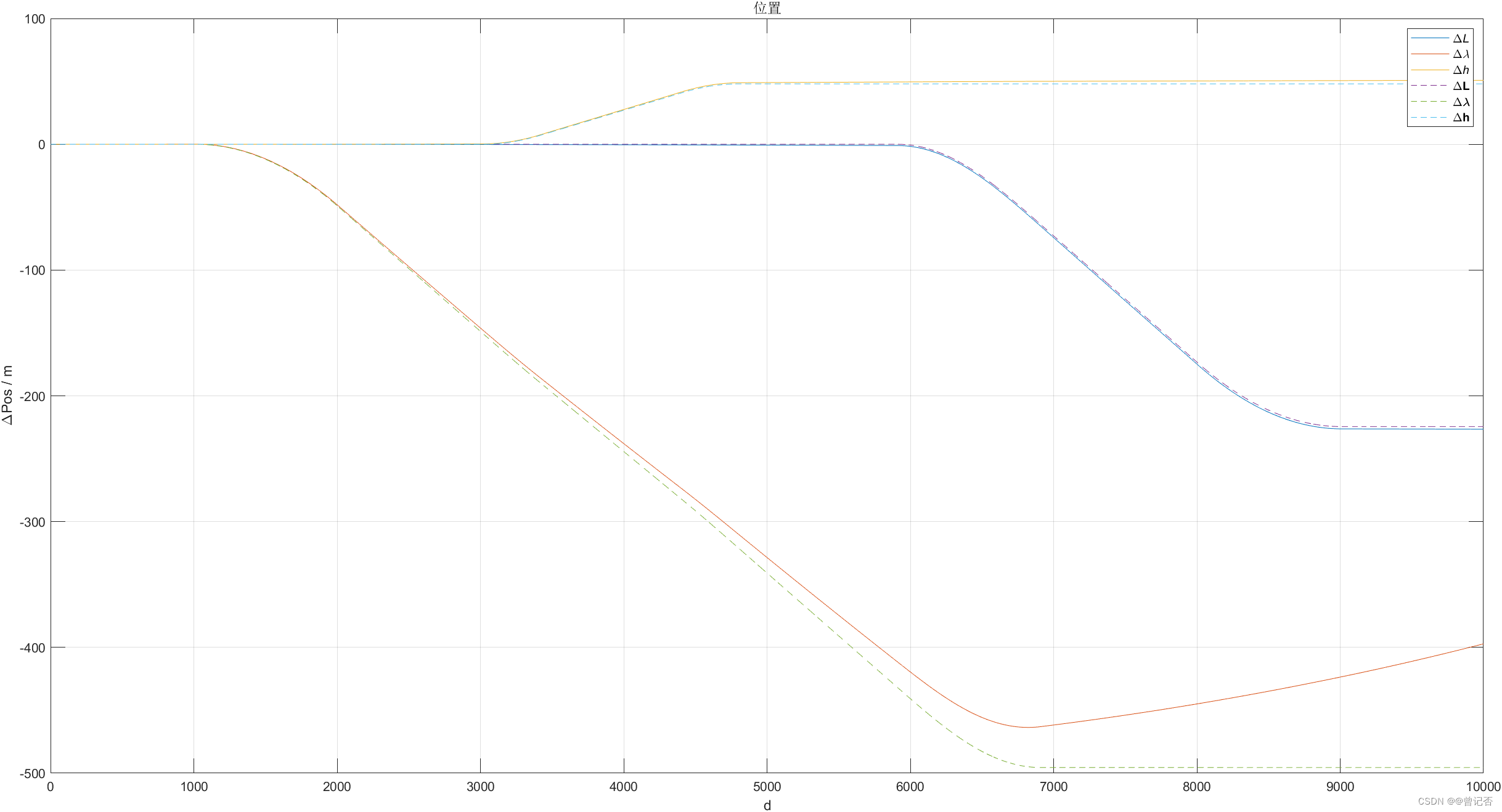
震荡原因与地球自转无关,是速度引起的经纬度变化:因为必须将速度项的单位化为弧度每秒,然后乘以时间得到与经纬度一致的弧度单位才能相加!!!!!


3、姿态更新

%%%%%%%%1.自己编写的没有加入地球自转所产生的误差补偿,经度位置增量偏小%%
q_bb = [cos(norm(delta_theta_m)/2);(delta_theta_m/norm(delta_theta_m))'*sin((norm(delta_theta_m)/2))];
q_nb2 = qmul(qnb,q_bb);
qnb = qnormlz(q_nb2);
%%%%%%%%2.在上一次的基础上加入地球自转补偿,即q_nn项%%%%%%%%%%%%%%%%%%
q_bb = [cos(norm(delta_theta_m)/2);(delta_theta_m/norm(delta_theta_m))'*sin((norm(delta_theta_m)/2))];
qnb = qmul(rv2q(-eth.wnin*nts), qmul(qnb, q_bb)); % 姿态更新
qnb = qnormlz(qnb);
4、程序仿真及实验结果
4.1 主函数
clc
clear
imu=load ('imu.mat'); %imu数据: avp=[wm, vm, tt(2:end)]; gx(rad) gy gz ax (m/s) ay az time
trj=load ('trj.mat'); %trj=[att, vn, pos]; att(度) vn(米每秒) pos(米)
arcdeg = pi/180;
nn=1; %子样数,采用二样子圆锥误差补偿算法
ts=0.01; %单个采样间隔的采样时间长度
nts=nn*ts; %采样周期,在nts时间内进行两次采样,每次采样 0.1秒
att = [0;0;90]*arcdeg; vn = [0;0;0]; pos = [[34;108]*arcdeg;100]; % att -- 欧拉角;arcdeg -- 度转换为弧度;vn -- 速度;pos -- 位置
% eth=earth(pos,vn);
% x=eth.clRNh*cos(pos(2));
% y=eth.clRNh*sin(pos(2));
% z=eth.RNeh*sin(pos(1));
% pos=[x;y;z];
qnb = a2qua(att);
len=length(imu.avp);
avps=zeros(fix(len/2),10);
avps(1,:)=[att;vn;pos;0]';
t=0;kk=1;
for k=1:nn:len %k是两次一跳,因为采用的是二子样,36000是6分钟开始解算
t=t+nts;
delta_theta_m=imu.avp(k,1:3);
delta_v_m=imu.avp(k,4:6);
[qnb,vn,pos]=insupdate(qnb,vn,pos,delta_theta_m,delta_v_m,ts);
cnb=q2att(qnb);
cnb(3)=mod(cnb(3),2*pi);
kk=kk+1;
avps(kk,:)=[cnb; vn; pos; t]'; %avp()=[θ γ ψ VE VN VU B L h t]
if mod(t,1)<nts, disp(fix(t));
end %显示进度 disp函数:显示文本或数组
end
%姿态
tt=length(avps);
tf=length(trj.trj);
figure(1);
subplot(211);
plot(1:tt,(avps(1:tt,1:2)/arcdeg),1:tf,(trj.trj(1:tf,1:2)/arcdeg),'--'); title('俯仰角和横滚角');xlabel('d');ylabel('\theta,\gamma(\circ)');
legend('\it\theta','\it\gamma','\bf\theta','\bf\gamma') ;grid on;
subplot(212);
plot(1:tt,(avps(1:tt,3)/arcdeg),1:tf,(trj.trj(1:tf,3)/arcdeg),'--'); title('偏航角');xlabel('d');ylabel('\Phi(\circ)');
legend('\it\Phi','\bf\Phi') ;grid on;
%速度
figure(2);
subplot(211);
plot(1:tt,(avps(1:tt,4:5)/arcdeg),1:tf,(trj.trj(1:tf,4:5)/arcdeg),'--'); title('速度');xlabel('d');ylabel('Vel/(m.s^{-1})');
legend('\itv\rm_E','\itv\rm_N','\bfv\rm_E','\bfv\rm_N')
subplot(212);grid on;
plot(1:tt,(avps(1:tt,6)/arcdeg),1:tf,(trj.trj(1:tf,6)/arcdeg),'--'); title('速度');xlabel('d');ylabel('Vel/(m.s^{-1})');
legend('\itv\rm_U','\bfv\rm_U');grid on;
%位置
figure(3);
plot(1:tt,deltapos(avps(1:tt,7:9)),1:tf,deltapos(trj.trj(1:tf,7:9)),'--'); title('位置');xlabel('d');ylabel('\DeltaPos / m');
legend('\Delta\itL', '\Delta\it\lambda', '\Delta\ith','\Delta\bfL', '\Delta\bf\lambda', '\Delta\bfh');grid on;
4.2 子函数
function [qnb,vn2,pos]=insupdate(qnb,vn1,pos,delta_theta_m,delta_v_m,ts)
nn=1; %子样数,采用二样子算法
nts=nn*ts;
g0=9.780325333434361; %单位;m/s^2
sl = sin(pos(1)); % pos(1)=L
sl2 = sl*sl; sl4 = sl2*sl2;
gLh = g0*(1+5.27094e-3*sl2+2.32718e-5*sl4)-3.086e-6*pos(3);
gn = [0;0;-gLh];
eth = earth(pos, vn1); % 地球相关参数计算
%速度更新
vsf =q2mat(qnb)*(delta_v_m + 1/2*cross(delta_theta_m,delta_v_m))'; %avp2(4:6) = avp1(4:6) + vsf + gn*Tm;
vn2 = vn1 + vsf + gn*nts;
%位置更新
%%%%%%%%2.速度项乘以Mpv(4-1.58)%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
vn1 = (vn2+vn1)/2;
pos = pos + [vn1(2)/eth.RMh;vn1(1)/eth.clRNh;vn1(3)]*nts;
%%%%%%%%1.按书上编写,未做修改,经度会产生剧烈震荡%%%%%%%%%%%%%%%%%%%%
% pos = pos+((vn1+vn2)/2)*nts; %avp2(7:9)=avp1(7:9)+(avp1(4:6)+avp2(4:6))*Tm/2;
%姿态更新 % q_nb1=att2qua(avp1(1:3));%姿态角转化为四元数
%%%%%%%%2.在上一次的基础上加入地球自转补偿,即q_nn项%%%%%%%%%%%%%%%%%%
q_bb = [cos(norm(delta_theta_m)/2);(delta_theta_m/norm(delta_theta_m))'*sin((norm(delta_theta_m)/2))];
qnb = qmul(rv2q(-eth.wnin*nts), qmul(qnb, q_bb)); % 姿态更新
qnb = qnormlz(qnb);
%%%%%%%%1.自己编写的没有加入地球自转所产生的误差补偿,经度位置增量偏小%%
% q_bb = [cos(norm(delta_theta_m)/2);(delta_theta_m/norm(delta_theta_m))'*sin((norm(delta_theta_m)/2))];
% q_nb2 = qmul(qnb,q_bb);
% qnb = qnormlz(q_nb2);
end
4.3 实验结果
1. 不考虑地球自转的影响
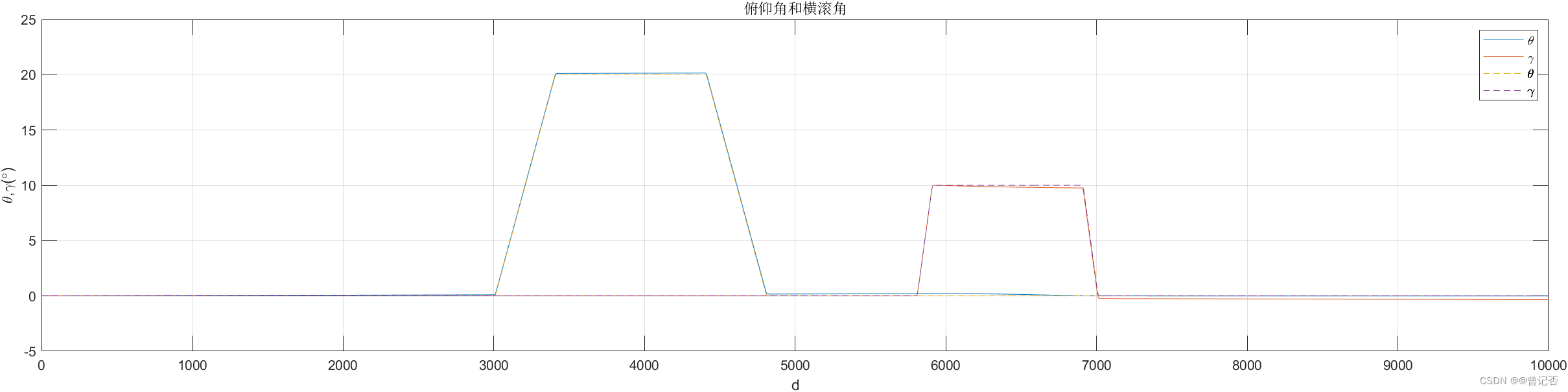
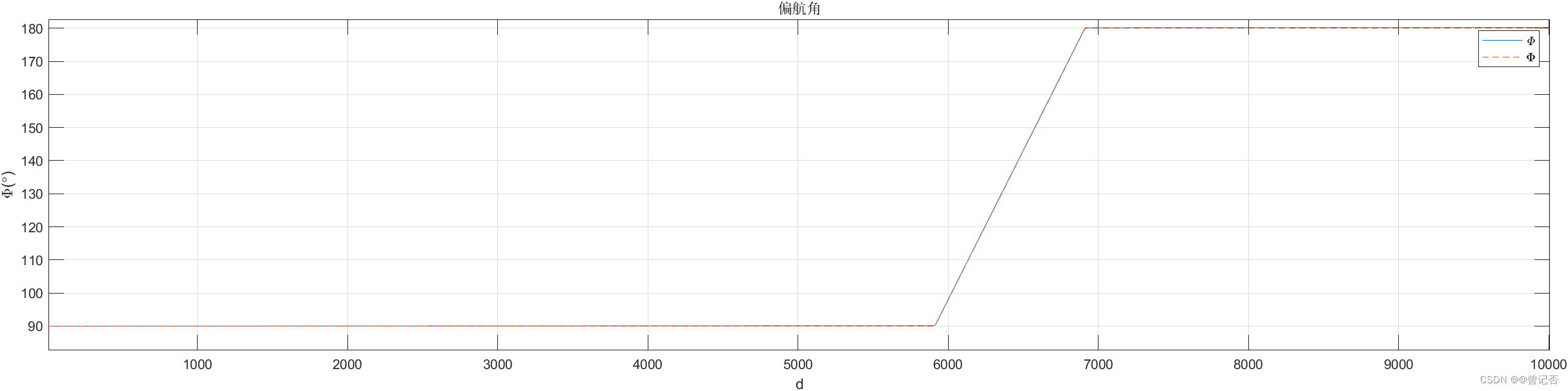
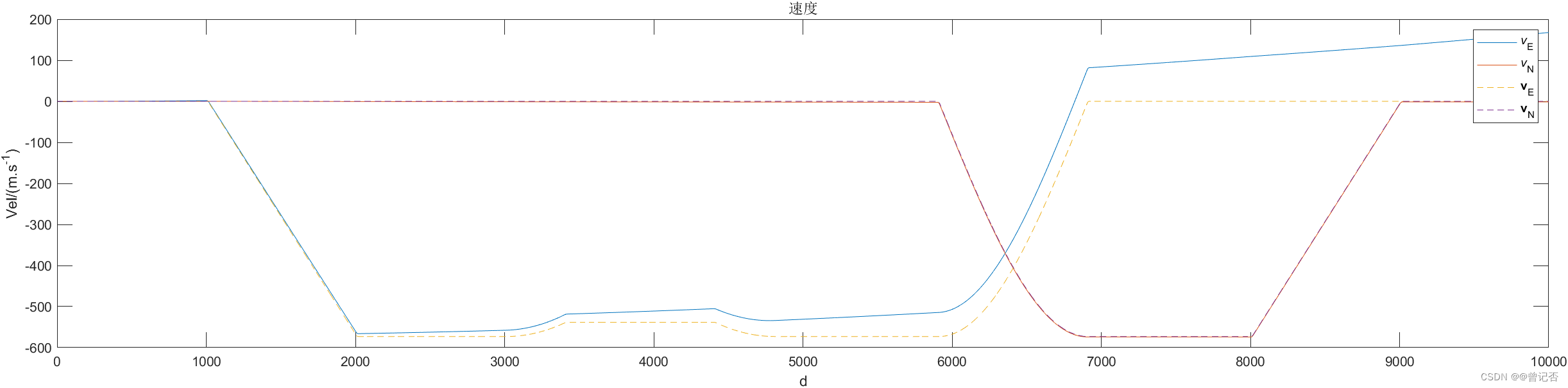
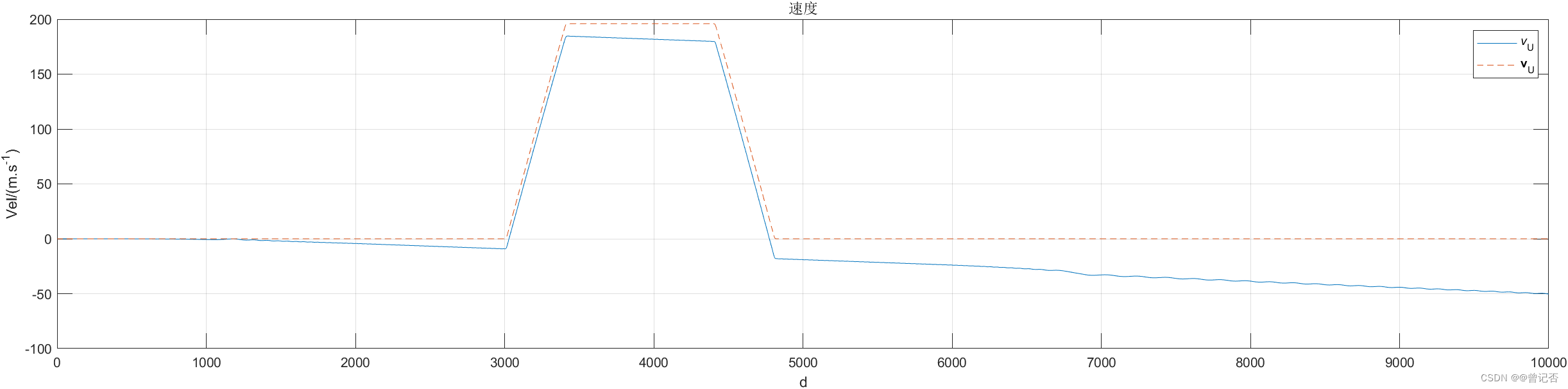

2. 考虑地球自转的影响
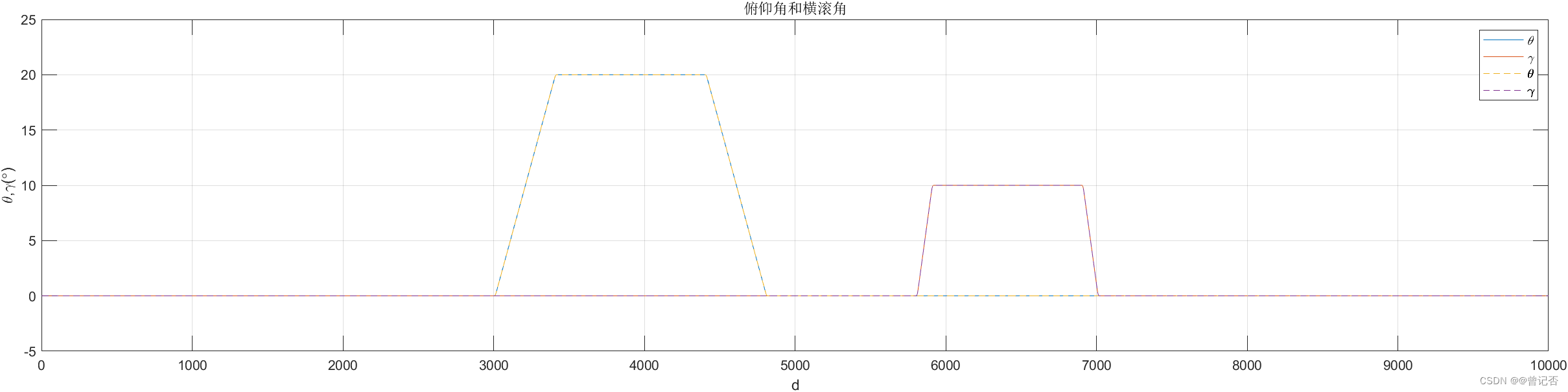
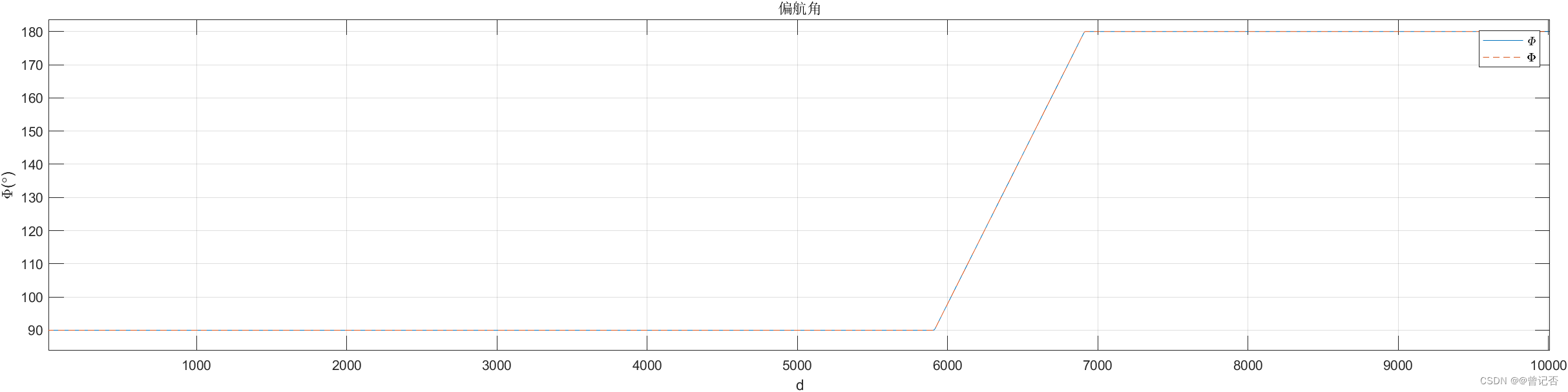
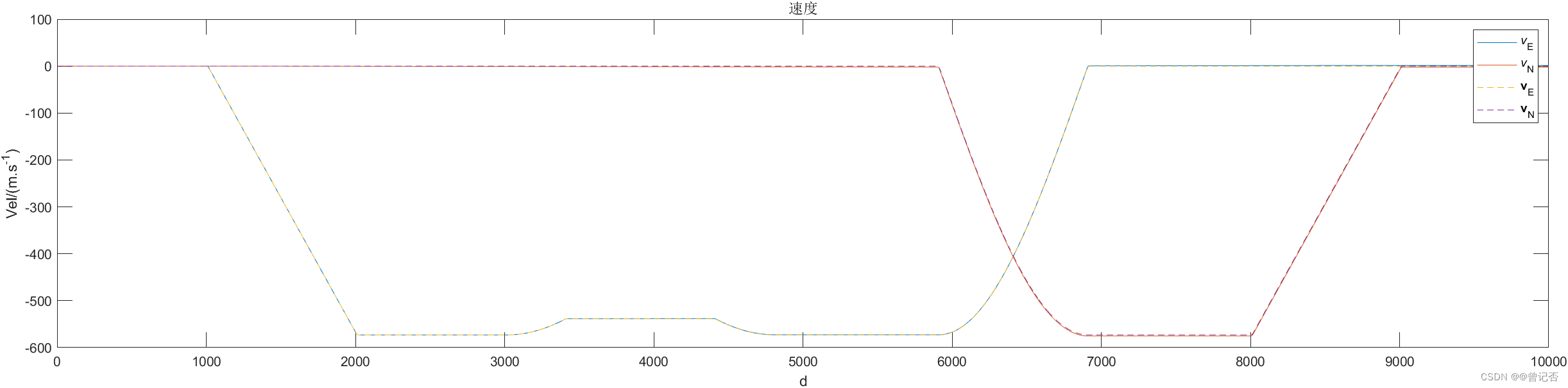
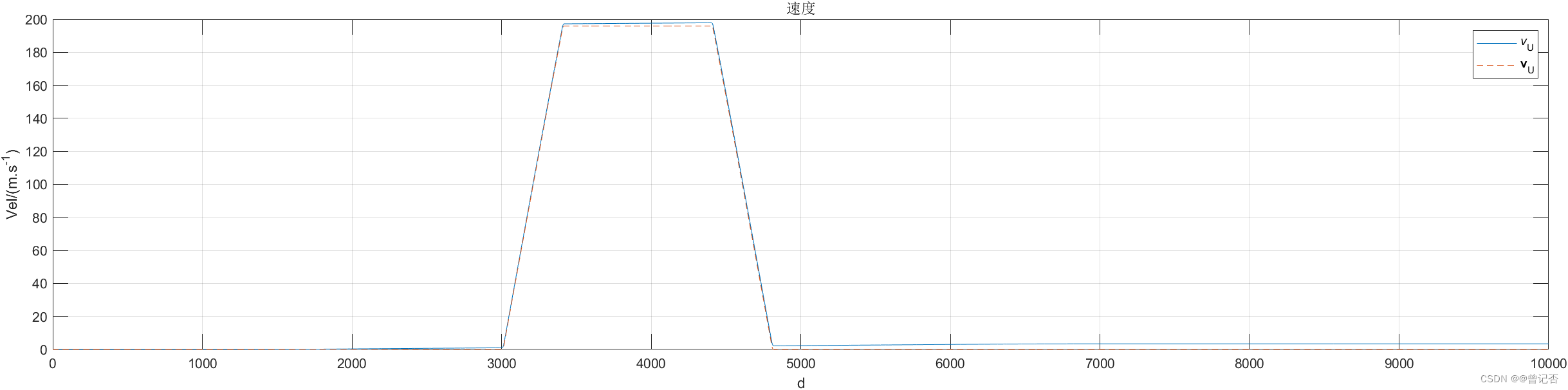
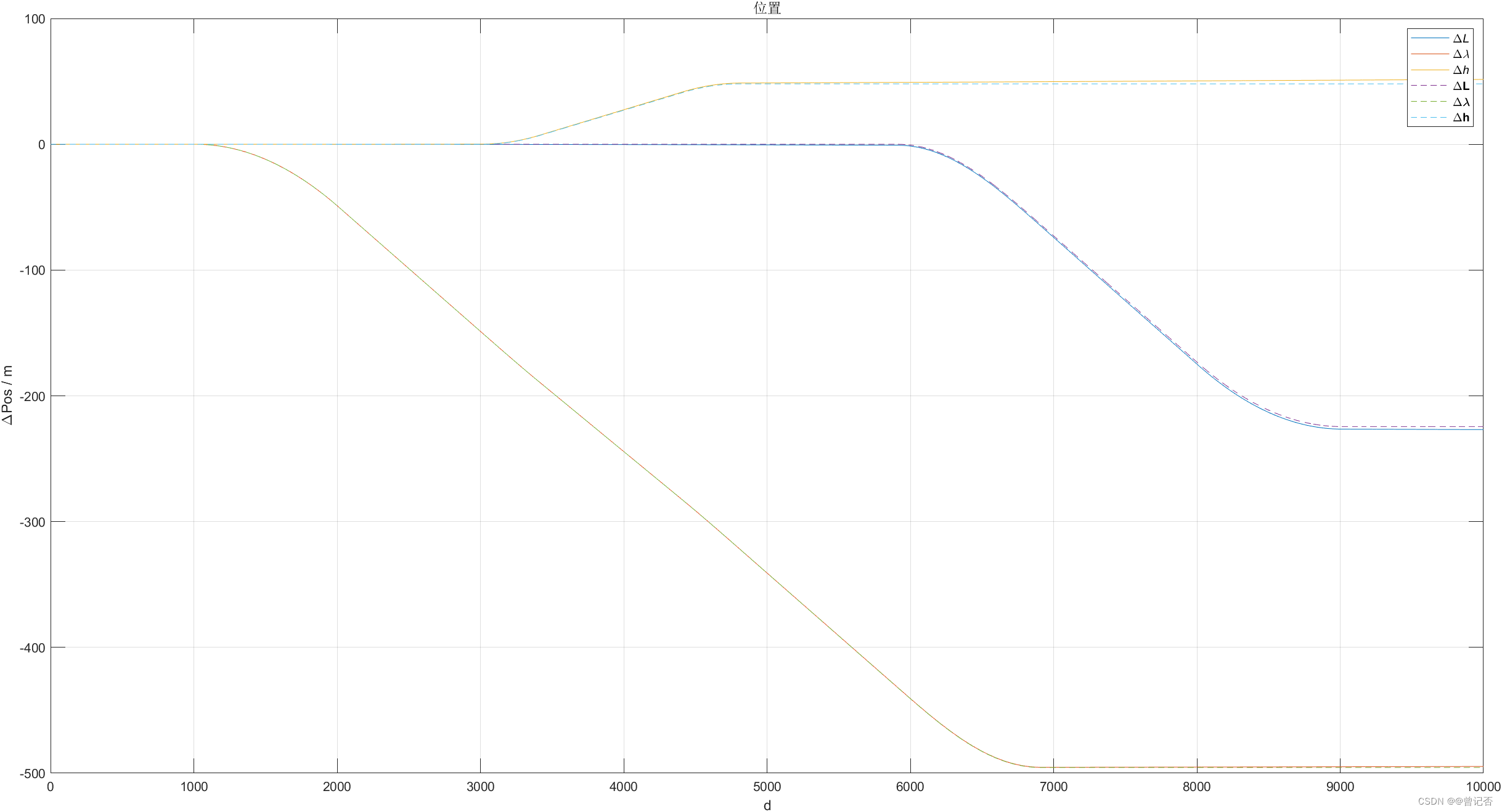
5. 程序代码及数据下载地址
https://download.csdn.net/download/qq_38364548/87364983