动态规划7.0
- 1. 最长公共子序列
- 2. 不相交的线
- 3. 不同的子序列
- 4. 通配符匹配
- 5. 正则表达式匹配
- 6. 交错字符串
- 7. 两个字符串的最小ASCII删除和
- 8. 最长重复子数组
1. 最长公共子序列
题目链接 -> Leetcode -1143.最长公共子序列
Leetcode -1143.最长公共子序列
题目:给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,“ace” 是 “abcde” 的子序列,但 “aec” 不是 “abcde” 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
示例 1:
输入:text1 = “abcde”, text2 = “ace”
输出:3
解释:最长公共子序列是 “ace” ,它的长度为 3 。
示例 2:
输入:text1 = “abc”, text2 = “abc”
输出:3
解释:最长公共子序列是 “abc” ,它的长度为 3 。
示例 3:
输入:text1 = “abc”, text2 = “def”
输出:0
解释:两个字符串没有公共子序列,返回 0 。
提示:
- 1 <= text1.length, text2.length <= 1000
- text1 和 text2 仅由小写英文字符组成
思路:
- 状态表示:对于两个数组的动态规划,我们的定义状态表示的经验就是:选取第一个数组 [0, i] 区间以及第二个数组 [0, j] 区间作为研究对象;结合题目要求,定义状态表示。在本题中,我们根据定义状态表示为:
- dp[i][j] 表示: s1 的 [0, i] 区间以及 s2 的 [0, j] 区间内的所有的子序列中,最长公共子序列的长度;
- 状态转移方程:分析状态转移方程的经验就是根据「最后一个位置」的状况,分情况讨论。对于 dp[i][j] ,我们可以根据 s1[i] 与 s2[j] 的字符分情况讨论:
- 两个字符相同, s1[i] = s2[j] :那么最长公共子序列就在 s1 的 [0, i - 1] 以及 s2 的 [0, j - 1] 区间上找到一个最长的,然后再加上 s1[i] 即可。因此 dp[i][j] = dp[i - 1][j - 1] + 1 ;
- 两个字符不相同, s1[i] != s2[j] :那么最长公共子序列一定不会同时以 s1[i] 和 s2[j] 结尾。那么我们找最长公共子序列时,有下面三种策略:
i. 去 s1 的 [0, i - 1] 以及 s2 的 [0, j] 区间内找:此时最大长度为 dp[i - 1][j] ;
ii. 去 s1 的 [0, i] 以及 s2 的 [0, j - 1] 区间内找:此时最大长度为 dp[i][j - 1] ;
iii. 去 s1 的 [0, i - 1] 以及 s2 的 [0, j - 1] 区间内找:此时最大长度为 dp[i - 1][j - 1] 。
我们要三者的最大值即可。但是我们细细观察会发现,第三种包含在第一种和第二种情况里面,但是我们求的是最大值,并不影响最终结果。因此只需求前两种情况下的最大值即可;
综上,状态转移方程为:
- if(s1[i] == s2[j]) dp[i][j] = dp[i - 1][j - 1] + 1 ;
- if(s1[i] != s2[j]) dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
- 返回值:根据「状态表示」得:返回 dp[m][n];
代码如下:
class Solution {
public:
int longestCommonSubsequence(string text1, string text2)
{
int m = text1.size(), n = text2.size();
// dp[i][j] 表示 test1中 0~i 和 test2中 0~j 字符串中最长公共子序列的长度
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
// 因为dp多开了一个空间,所以使字符串统一向后移动一个单位,使下标一一对应
text1 = ' ' + text1, text2 = ' ' + text2;
for(int i = 1; i <= m; i++)
{
for(int j = 1; j <= n; j++)
{
// 最后两个字符相同的话,一定是公共子序列
if(text1[i] == text2[j]) dp[i][j] = dp[i - 1][j - 1] + 1;
// 否则取test1中0~i-1 的字符串和test2中 0~j 的字符串 和 test1中 0~i 的字符串和test2中 0~j-1 的字符串的dp表中的较大值
else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
return dp[m][n];
}
};
2. 不相交的线
题目链接 -> Leetcode -1035.不相交的线
Leetcode -1035.不相交的线
题目:在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。
现在,可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线,这些直线需要同时满足满足:
nums1[i] == nums2[j]
且绘制的直线不与任何其他连线(非水平线)相交。
请注意,连线即使在端点也不能相交:每个数字只能属于一条连线。
以这种方法绘制线条,并返回可以绘制的最大连线数。
示例 1:
输入:nums1 = [1, 4, 2], nums2 = [1, 2, 4]
输出:2
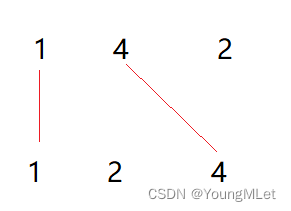
解释:可以画出两条不交叉的线,如上图所示。
但无法画出第三条不相交的直线,因为从 nums1[1] = 4 到 nums2[2] = 4 的直线将与从 nums1[2] = 2 到 nums2[1] = 2 的直线相交。
示例 2:
输入:nums1 = [2, 5, 1, 2, 5], nums2 = [10, 5, 2, 1, 5, 2]
输出:3
示例 3:
输入:nums1 = [1, 3, 7, 1, 7, 5], nums2 = [1, 9, 2, 5, 1]
输出:2
提示:
- 1 <= nums1.length, nums2.length <= 500
- 1 <= nums1[i], nums2[j] <= 2000
思路:如果要保证两条直线不相交,那么我们「下一个连线」必须在「上一个连线」对应的两个元素的「后面」寻找相同的元素。这就转化成「最长公共子序列」的模型了。那就是在这两个数组中寻找「最长的公共子序列」。
代码如下:
class Solution {
public:
// 与最长公共子序列同类型
int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2)
{
int m = nums1.size(), n = nums2.size();
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
for(int i = 1; i <= m; i++)
{
for(int j = 1; j <= n; j++)
{
if(nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
return dp[m][n];
}
};
3. 不同的子序列
题目链接 -> Leetcode -115.不同的子序列
Leetcode -115.不同的子序列
题目:给你两个字符串 s 和 t ,统计并返回在 s 的 子序列 中 t 出现的个数,结果需要对 10^9 + 7 取模。
示例 1:
输入:s = “rabbbit”, t = “rabbit”
输出:3
解释:
如下所示, 有 3 种可以从 s 中得到 “rabbit” 的方案。
rabbbit
rabbbit
rabbbit
示例 2:
输入:s = “babgbag”, t = “bag”
输出:5
解释:
如下所示, 有 5 种可以从 s 中得到 “bag” 的方案。
babgbag
babgbag
babgbag
babgbag
babgbag
提示:
- 1 <= s.length, t.length <= 1000
- s 和 t 由英文字母组成
思路:
- 状态表示:对于两个字符串之间的 dp 问题,我们一般的思考方式如下:
- 选取第一个字符串的 [0, i] 区间以及第二个字符串的 [0, j] 区间当成研究对象,结合题目的要求来定义「状态表示」;
- 然后根据两个区间上「最后一个位置的字符」,来进行「分类讨论」,从而确定「状态转移方程」。
我们可以根据上面的策略,解决大部分关于两个字符串之间的 dp 问题。
- dp[i][j] 表示:在字符串 s 的 [0, j] 区间内的所有子序列中,有多少个 t 字符串 [0, i] 区间内的子串;
- 状态转移方程:根据「最后一个位置」的元素,结合题目要求,分情况讨论:
- 当 t[i] == s[j] 的时候,此时的子序列有两种选择:
i. 一种选择是:子序列选择 s[j] 作为结尾,此时相当于在状态 dp[i - 1][j - 1]
中的所有符合要求的子序列的后面,再加上一个字符 s[j] ,此时 dp[i][j] = dp[i - 1][j - 1] ;
ii. 另一种选择是:不选择 s[j] 作为结尾;此时相当于选择了状态 dp[i][j - 1] 中所有符合要求的子序列。我们也可以理解为继承了上个状态里面的求得的子序列。此时 dp[i][j] = dp[i][j - 1] ;
两种情况加起来,就是 t[i] == s[j] 时的结果。
- 当 t[i] != s[j] 的时候,此时的子序列只能从 dp[i][j - 1] 中选择所有符合要求的子序列。只能继承上个状态里面求得的子序列,dp[i][j] = dp[i][j - 1] ;
综上所述,状态转移方程为:
- 所有情况下都可以继承上一次的结果: dp[i][j] = dp[i][j - 1] ;
- 当 t[i] == s[j] 时,可以多选择一种情况: dp[i][j] += dp[i - 1][j - 1]
- 返回值:根据「状态表示」,返回 dp[m][n] 的值;
代码如下:
class Solution {
public:
int numDistinct(string s, string t)
{
int m = t.size(), n = s.size();
// dp[i][j] 表示,s字符串[0,j]区间内所有的子序列中,有多少个t字符串[0,i]区间内的子串
// 多开一行一列,引入空串
vector<vector<double>> dp(m + 1, vector<double>(n + 1));
// 当 s 为空串时,t 中怎么也会有一个空串,所以将第一行全部初始化为1
for (int j = 0; j <= n; j++) dp[0][j] = 1;
s = " " + s, t = " " + t; // 使下标一一对应
for (int i = 1; i <= m; i++)
{
for (int j = 1; j <= n; j++)
{
// 不算当前 s[j] ,统计s中 0~j-1 组成的字符串中有多少能组成 t 中0~i的子序列
dp[i][j] += dp[i][j - 1];
// 算当前 s[j],当 s[j] == t[i] 时再算上前面的子序列累加起来
if (s[j] == t[i]) dp[i][j] += dp[i - 1][j - 1];
}
}
return dp[m][n];
}
};
4. 通配符匹配
题目链接 -> Leetcode -44.通配符匹配
Leetcode -44.通配符匹配
题目:给你一个输入字符串(s) 和一个字符模式( p),请你实现一个支持 ‘?’ 和 ’ * ’ 匹配规则的通配符匹配:
‘?’ 可以匹配任何单个字符。
’ * ’ 可以匹配任意字符序列(包括空字符序列)。
判定匹配成功的充要条件是:字符模式必须能够 完全匹配 输入字符串(而不是部分匹配)。
示例 1:
输入:s = “aa”, p = “a”
输出:false
解释:“a” 无法匹配 “aa” 整个字符串。
示例 2:
输入:s = “aa”, p = “*”
输出:true
解释:’ * ’ 可以匹配任意字符串。
示例 3:
输入:s = “cb”, p = “?a”
输出:false
解释:‘?’ 可以匹配 ‘c’, 但第二个 ‘a’ 无法匹配 ‘b’。
提示:
- 0 <= s.length, p.length <= 2000
- s 仅由小写英文字母组成
- p 仅由小写英文字母、‘?’ 或 ‘*’ 组成
思路:
- 状态表示:对于两个字符串之间的 dp 问题,我们一般的思考方式如下:
- 选取第一个字符串的 [0, i] 区间以及第二个字符串的 [0, j] 区间当成研究对象,结合题目的要求来定义「状态表示」;
- 然后根据两个区间上「最后一个位置的字符」,来进行「分类讨论」,从而确定「状态转移方程」。
因此,我们定义状态表示为:dp[i][j] 表示: p 字符串 [0, j] 区间内的子串能否匹配字符串 s 的 [0, i] 区间内的子串。
- 状态转移方程:
我们根据最后一个位置的元素,结合题目要求,分情况讨论:
- 当 s[i] == p[j] 或 p[j] == ‘?’ 的时候,此时两个字符串匹配上了当前的一个字符,只能从 dp[i - 1][j - 1] 中看当前字符前面的两个子串是否匹配。只能继承上个状态中的匹配结果, dp[i][j] = dp[i][j - 1] ;
- 当 p[j] == ‘*’ 的时候,此时匹配策略有两种选择:
i. 一种选择是: * 匹配空字符串,此时相当于它什么都没有匹配,直接继承状态 dp[i][j - 1] ,此时 dp[i][j] = dp[i][j - 1] ;
ii. 另⼀种选择是: * 向前匹配 1 ~ n 个字符,直至匹配上整个 s1 串。此时相当于从 dp[k][j - 1] (0 <= k <= i) 中所有匹配情况中,选择性继承可以成功的情况。此时 dp[i][j] = dp[k][j - 1] (0 <= k <= i) ; - 当 p[j] 不是特殊字符,且不与 s[i] 相等时,无法匹配。
三种情况加起来,就是所有可能的匹配结果。
即下图分析:
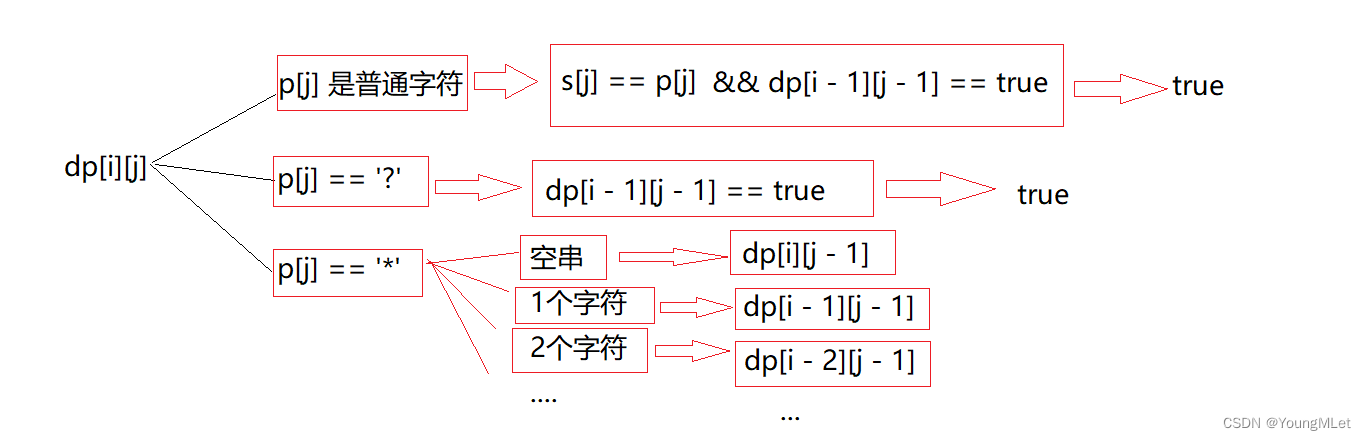
综上所述,状态转移方程为:
- 当 s[i] == p[j] 或 p[j] == ‘?’ 时: dp[i][j] = dp[i][j - 1] ;
- 当 p[j] == ‘*’ 时,有多种情况需要讨论: dp[i][j] = dp[k][j - 1] (0 <= k <= i) ;
优化:当我们发现,计算一个状态的时候,需要一个循环才能搞定的时候,我们要想到去优化。优化的方向就是用一个或者两个状态来表示这一堆的状态。通常就是把它写下来,然后用数学的方式做一下等价替换:
当 p[j] == ‘*’ 时,状态转移方程为:
dp[i][j] = dp[i][j - 1] || dp[i - 1][j - 1] || dp[i - 2][j - 1] || …
我们发现 i 是有规律的减小的,因此我们去看看 dp[i - 1][j] :
dp[i - 1][j] = dp[i - 1][j - 1] || dp[i - 2][j - 1] || dp[i - 3][j - 1] …
我们发现, dp[i][j] 的状态转移方程里面除了第一项以外,其余的都可以用 dp[i - 1][j] 替代。因此,我们优化我们的状态转移方程为: dp[i][j] = dp[i - 1][j] || dp[i][j - 1].
- 初始化:
由于 dp 数组的值设置为是否匹配,为了不与答案值混淆,我们需要将整个数组初始化为 false;由于需要用到前一行和前一列的状态,我们初始化第一行、第一列即可;
- dp[0][0] 表示两个空串能否匹配,答案是显然的, 初始化为 true.
- 第一行表示 s 是一个空串, p 串和空串只有一种匹配可能,即 p 串表示为 *** ,此时也相当于空串匹配上空串。所以,我们可以遍历 p 串,把所有前导为 “*” 的 p 子串和空串的 dp 值设为 true.
- 第一列表示 p 是一个空串,不可能匹配上 s 串,跟随数组初始化即可.
- 返回值:根据状态表示,返回 dp[m][n] 的值.
代码如下:
class Solution {
public:
bool isMatch(string s, string p)
{
int m = s.size(), n = p.size();
s = ' ' + s, p = ' ' + p;
// dp[i][j] 表示: p 字符串 [0, j] 区间内的⼦串能否匹配字符串 s 的 [0, i] 区间内的⼦串。
vector<vector<bool>> dp(m + 1, vector<bool>(n + 1));
// 完成初始化
// 多开一行一列,第一行相当于s为空串,第一列相当于p为空串
dp[0][0] = true; // 大家都是空串,可以匹配
for(int i = 1; i <= n; i++)
if(p[i] == '*') dp[0][i] = true; // 在第一行中初始化中,只要 p 中出现不是'*'就不匹配
else break;
for(int i = 1; i <= m; i++)
{
for(int j = 1; j <= n; j++)
{
// 状态转移方程,分析 dp[i][j]等于什么,分情况讨论
if(p[j] == '?' && dp[i - 1][j - 1]) dp[i][j] = true; // 当 p[j] 是 '?' 时
else if(p[j] == '*') dp[i][j] = dp[i][j - 1] || dp[i - 1][j]; // 当p[j]是 '*' 时,用数学推算出来
else if(p[j] == s[i] && dp[i - 1][j - 1]) dp[i][j] = true; // 当p[j] 等于 s[i] 时
}
}
return dp[m][n];
}
};
5. 正则表达式匹配
题目链接 -> Leetcode -10.正则表达式匹配
Leetcode -10.正则表达式匹配
题目:给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 ‘.’ 和 ‘*’ 的正则表达式匹配。
‘.’ 匹配任意单个字符
‘*’ 匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。
示例 1:
输入:s = “aa”, p = “a”
输出:false
解释:“a” 无法匹配 “aa” 整个字符串。
示例 2:
输入:s = “aa”, p = “a*”
输出:true
解释:因为 ‘*’ 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 ‘a’。因此,字符串 “aa” 可被视为 ‘a’ 重复了一次。
示例 3:
输入:s = “ab”, p = “.*”
输出:true
解释:". * " 表示可匹配零个或多个(’ * ‘)任意字符(’.')。
提示:
- 1 <= s.length <= 20
- 1 <= p.length <= 20
- s 只包含从 a - z 的小写字母。
- p 只包含从 a - z 的小写字母,以及字符.和 * 。
- 保证每次出现字符 * 时,前面都匹配到有效的字符
思路:
- 状态表示:dp[i][j] 表示:字符串 p 的 [0, j] 区间和字符串 s 的 [0, i] 区间是否可以匹配;
- 状态转移方程:根据最后⼀个位置的元素,结合题⽬要求,分情况讨论:
- 当 s[i] == p[j] 或 p[j] == ‘.’ 的时候,此时两个字符串匹配上了当前的⼀个字符,只能从 dp[i - 1][j - 1] 中看当前字符前⾯的两个⼦串是否匹配。只能继承上个状态中的匹配结果, dp[i][j] = dp[i - 1][j - 1] ;
- 当 p[j] == '’ 的时候,和上道题稍有不同的是,上道题 "" 本⾝便可匹配 0 ~ n 个字符,但此题是要带着 p[j - 1] 的字符⼀起,匹配 0 ~ n 个和 p[j - 1] 相同的字符。此时,匹配策略有两种选择:
a. ⼀种选择是: p[j - 1]* 匹配空字符串,此时相当于这两个字符都没有撇配,直接继承状态 dp[i][j - 2] ,此时 dp[i][j] = dp[i][j - 2] ;
b. 另⼀种选择是: p[j - 1]* 向前匹配 1 ~ n 个字符,直⾄匹配上整个 s1 串;此时相当于从 dp[k][j - 2] (0 < k <= i) 中所有匹配情况中,选择性继承可以成功的情况。此时 dp[i][j] = dp[k][j - 2] (0 < k <= i 且 s[k]~s[i] = p[j - 1]) ; - 当 p[j] 不是特殊字符,且不与 s[i] 相等时,无法匹配。
三种情况加起来,就是所有可能的匹配结果。
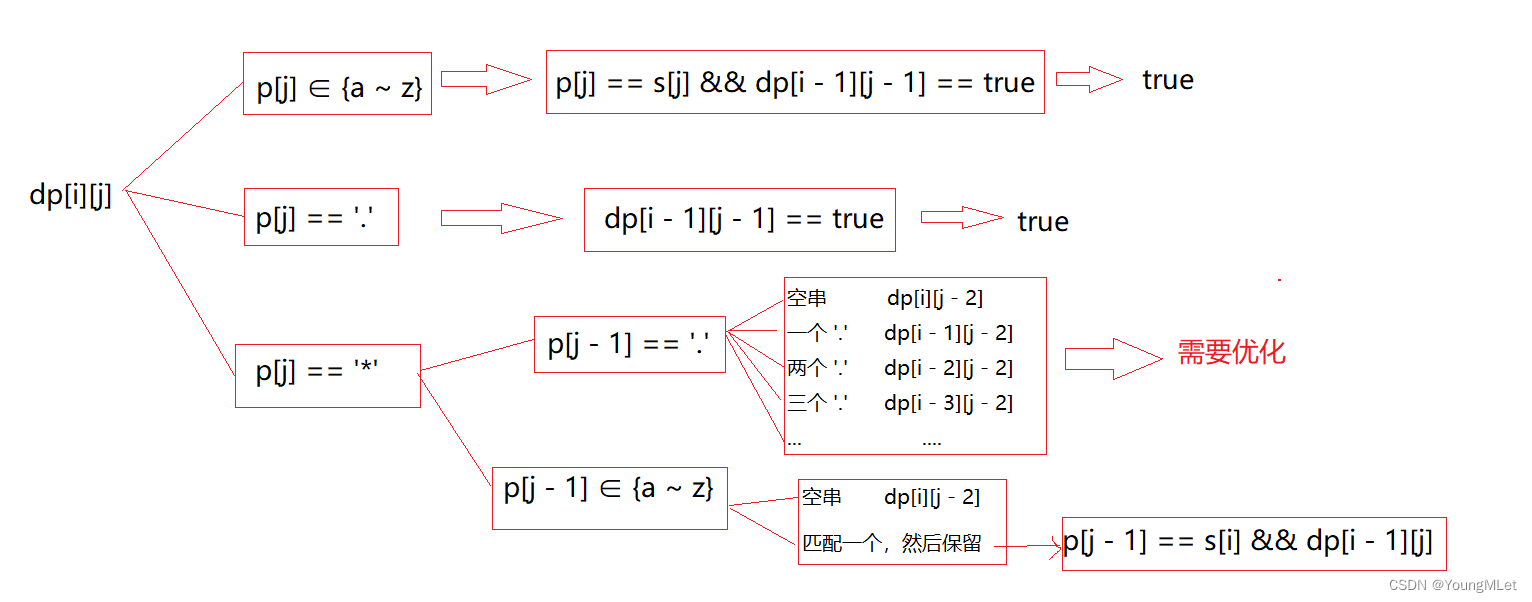
综上所述,状态转移方程为:
- 当 s[i] == p[j] 或 p[j] == ‘.’ 时: dp[i][j] = dp[i][j - 1] ;
- 当 p[j] == ‘*’ 时,有多种情况需要讨论: dp[i][j] = dp[i][j - 2] ;dp[i][j] = dp[k][j - 1] (0 <= k <= i)
优化:当我们发现,计算一个状态的时候,需要一个循环才能搞定的时候,我们要想到去优化。优化的方向就是用一个或者两个状态来表示这一堆的状态。通常就是把它写下来,然后用数学的方式做一下等价替换:
当 p[j] == ‘*’ 时,状态转移方程为:
dp[i][j] = dp[i][j - 2] || dp[i - 1][j - 2] || dp[i - 2][j - 2] …
我们发现 i 是有规律的减小的,因此我们去看看 dp[i - 1][j] :
dp[i - 1][j] = dp[i - 1][j - 2] || dp[i - 2][j - 2] || dp[i - 3][j - 2] …
我们发现, dp[i][j] 的状态转移方程里面除了第一项以外,其余的都可以用 dp[i - 1][j] 替代。因此,我们优化我们的状态转移方程为: dp[i][j] = dp[i][j - 2] || dp[i - 1][j] .
- 初始化:
由于 dp 数组的值设置为是否匹配,为了不与答案值混淆,我们需要将整个数组初始化为 false.
由于需要用到前一行和前一列的状态,我们初始化第一行、第一列即可;dp[0][0] 表示两个空串能否匹配,答案是显然的, 初始化为 true;第一行表示 s 是一个空串, p 串和空串只有一种匹配可能,即 p 串全部字符表示为 “任⼀字符+ *”,此时也相当于空串匹配上空串。所以,我们可以遍历 p 串,把所有前导为 "任⼀字符 + *"的 p 子串和空串的 dp 值设为 true.
- 返回值:根据状态表示,返回 dp[m][n] 的值.
代码如下:
class Solution {
public:
bool isMatch(string s, string p)
{
int m = s.size(), n = p.size();
// dp[i][j] 表⽰,字符串 p 的 [0, j] 区间和字符串 s 的 [0, i] 区间是否可以匹配
vector<vector<bool>> dp(m + 1, vector<bool>(n + 1));
s = ' ' + s, p = ' ' + p;
// 完成初始化
// 第⼀⾏表⽰ s 是⼀个空串, p 串和空串只有⼀种匹配可能,即 p 串全部字符表⽰为 "任⼀字符+ *",此时也相当于空串匹配上空串。所以,我们可以遍历 p 串,把所有前导为 "任⼀字符 + *"的 p ⼦串和空串的 dp 值设为 true 。因为 "任⼀字符+ *" 可以表示空串
dp[0][0] = true;
for(int i = 2; i <= n; i += 2)
if(p[i] == '*') dp[0][i] = true, dp[0][i - 1] = true;
else break;
for(int i = 1; i <= m; i++)
{
for(int j = 1; j <= n; j++)
{
// dp[i][j] = dp[i][j - 2] || dp[i - 1][j] 使用数学推导
// dp[i][j - 2] 不会报错是因为第一个位置不可能是'*'
if(p[j] == '*')
dp[i][j] = dp[i][j - 2] || dp[i - 1][j] && (p[j - 1] == s[i] || p[j - 1] == '.');
else
dp[i][j] = ((p[j] == s[i] || p[j] == '.') && dp[i - 1][j - 1]);
}
}
return dp[m][n];
}
};
6. 交错字符串
题目链接 -> Leetcode -97.交错字符串
Leetcode -97.交错字符串
题目:给定三个字符串 s1、s2、s3,请你帮忙验证 s3 是否是由 s1 和 s2 交错 组成的。
两个字符串 s 和 t 交错 的定义与过程如下,其中每个字符串都会被分割成若干 非空 子字符串:
s = s1 + s2 + … + sn
t = t1 + t2 + … + tm
| n - m| <= 1
交错 是 s1 + t1 + s2 + t2 + s3 + t3 + … 或者 t1 + s1 + t2 + s2 + t3 + s3 + …
注意:a + b 意味着字符串 a 和 b 连接。
示例 1:
输入:s1 = “aabcc”, s2 = “dbbca”, s3 = “aadbbcbcac”
输出:true
示例 2:
输入:s1 = “aabcc”, s2 = “dbbca”, s3 = “aadbbbaccc”
输出:false
示例 3:
输入:s1 = “”, s2 = “”, s3 = “”
输出:true
提示:
- 0 <= s1.length, s2.length <= 100
- 0 <= s3.length <= 200
- s1、s2、和 s3 都由小写英文字母组成
思路:
- 状态表示:dp[i][j] 表示字符串 s1 中 [1, i] 区间内的字符串以及 s2 中 [1, j] 区间内的字符串,能否拼接成 s3 中 [1, i + j] 区间内的字符串;
- 状态转移方程:
先分析一下题目,题目中交错后的字符串为 s1 + t1 + s2 + t2 + s3 + t3… ,看似一个 s 一个 t 。实际上 s1 能够拆分成更小的一个字符,进而可以细化成 s1 + s2 + s3 + t1 + t2 + s4… ;也就是说,并不是前一个用了 s 的子串,后一个必须要用 t 的子串。这一点理解,对我们的状态转移很重要。
继续根据两个区间上「最后一个位置的字符」,结合题目的要求,来进行「分类讨论」:
- 当 s3[i + j] = s1[i] 的时候,说明交错后的字符串的最后一个字符和 s1 的最后一个字符匹配了。那么整个字符串能否交错组成,变成:s1 中 [1, i - 1] 区间上的字符串以及 s2 中 [1, j] 区间上的字符串,能够交错形成 s3 中 [1, i + j - 1] 区间上的字符串,也就是 dp[i - 1][j] ;此时 dp[i][j] = dp[i - 1][j];
- 当 s3[i + j] = s2[j] 的时候,说明交错后的字符串的最后一个字符和 s2 的最后一个字符匹配了。那么整个字符串能否交错组成,变成:s1 中 [1, i] 区间上的字符串以及 s2 中 [1, j - 1] 区间上的字符串,能够交错形成 s3 中 [1, i + j - 1] 区间上的字符串,也就是 dp[i][j - 1] ;
- 当两者的末尾都不等于 s3 最后一个位置的字符时,说明不可能是两者的交错字符串。
上述三种情况下,只要有一个情况下能够交错组成目标串,就可以返回 true;因此,我们可以定义状态转移为:
- dp[i][j] = (s1[i - 1] == s3[i + j - 1] && dp[i - 1][j]) || (s2[j - 1] == s3[i + j - 1] && dp[i][j - 1])
- 初始化:
由于用到 i - 1 , j - 1 位置的值,因此需要初始化「第一个位置」以及「第一行」和「第一列」。
- 第一个位置:dp[0][0] = true ,因为空串 + 空串能够构成一个空串。
- 第一行:第一行表示 s1 是一个空串,我们只用考虑 s2 即可。因此状态转移之和 s2 有关:dp[0][j] = s2[j - 1] == s3[j - 1] && dp[0][j - 1] , j 从 1 到 n( n 为 s2 的长度)
- 第一列:第一列表示 s2 是一个空串,我们只用考虑 s1 即可。因此状态转移之和 s1 有关:dp[i][0] = s1[i - 1] == s3[i - 1] && dp[i - 1][0] , i 从 1 到 m( m 为 s1 的长度)
- 返回值:根据「状态表示」,我们需要返回 dp[m][n] 的值。
代码如下:
class Solution {
public:
bool isInterleave(string s1, string s2, string s3)
{
int l1 = s1.size(), l2 = s2.size(), l3 = s3.size();
if(l1 + l2 != l3) return false;
s1 = " " + s1, s2 = " " + s2, s3 = " " + s3;
// 完成初始化
// dp[i][j] 表⽰字符串 s1 中 [1, i] 区间内的字符串以及 s2 中 [1, j] 区间内的字符串,能否拼接成 s3 中 [1, i + j] 区间内的字符串
vector<vector<bool>> dp(l1 + 1, vector<bool>(l2 + 1));
dp[0][0] = true;
// 第⼀⾏表⽰ s1 是⼀个空串,我们只⽤考虑 s2 即可
for(int j = 1; j <= l2; j++)
if(s2[j] == s3[j]) dp[0][j] = true;
else break;
// 第⼀列表⽰ s2 是⼀个空串,我们只⽤考虑 s1 即可
for(int i = 1; i <= l1; i++)
if(s1[i] == s3[i]) dp[i][0] = true;
else break;
// 开始填表
for(int i = 1; i <= l1; i++)
{
for(int j = 1; j <= l2; j++)
{
// 比较 s1 和 s2 中最后一个字符和 s3 中最后一个字符是否相同
dp[i][j] = (s1[i] == s3[i + j] && dp[i - 1][j]) ||
(s2[j] == s3[i + j] && dp[i][j - 1]);
}
}
return dp[l1][l2];
}
};
7. 两个字符串的最小ASCII删除和
题目链接 -> Leetcode -712.两个字符串的最小ASCII删除和
Leetcode -712.两个字符串的最小ASCII删除和
题目:给定两个字符串s1 和 s2,返回 使两个字符串相等所需删除字符的 ASCII 值的最小和 。
示例 1:
输入: s1 = “sea”, s2 = “eat”
输出 : 231
解释 : 在 “sea” 中删除 “s” 并将 “s” 的值(115)加入总和。
在 “eat” 中删除 “t” 并将 116 加入总和。
结束时,两个字符串相等,115 + 116 = 231 就是符合条件的最小和。
示例 2 :
输入 : s1 = “delete”, s2 = “leet”
输出 : 403
解释 : 在 “delete” 中删除 “dee” 字符串变成 “let”,
将 100[d] + 101[e] + 101[e] 加入总和。在 “leet” 中删除 “e” 将 101[e] 加入总和。
结束时,两个字符串都等于 “let”,结果即为 100 + 101 + 101 + 101 = 403 。
如果改为将两个字符串转换为 “lee” 或 “eet”,我们会得到 433 或 417 的结果,比答案更大。
提示 :
- 0 <= s1.length, s2.length <= 1000
- s1 和 s2 由小写英文字母组成
思路:正难则反,求两个字符串的最小 ASCII 删除和,其实就是找到两个字符串中所有的公共子序列里面, ASCII 最大和。因此,我们的思路就是按照「最长公共子序列」的分析方式来分析。
- 状态表示:dp[i][j] 表示: s1 的 [0, i] 区间以及 s2 的 [0, j] 区间内的所有的子序列中,公共子序列的 ASCII 最大和。
- 状态转移方程:
对于 dp[i][j] 根据「最后一个位置」的元素,结合题目要求,分情况讨论:
- 当 s1[i] == s2[j] 时:应该先在 s1 的 [0, i - 1] 区间以及 s2 的 [0, j - 1] 区间内找一个公共子序列的最大和,然后在它们后面加上一个 s1[i] 字符即可。
此时 dp[i][j] = dp[i - 1][j - 1] + s1[i] ; - 当 s1[i] != s2[j] 时:公共子序列的最大和会有三种可能:
(1) s1 的 [0, i - 1] 区间以及 s2 的 [0, j] 区间内:此时 dp[i][j] = dp[i - 1][j] ;
(2) s1 的 [0, i] 区间以及 s2 的 [0, j - 1] 区间内:此时 dp[i][j] = dp[i][j - 1] ;
(3) s1 的 [0, i - 1] 区间以及 s2 的 [0, j - 1] 区间内:此时 dp[i][j] = dp[i - 1][j - 1] ;
但是前两种情况里面包含了第三种情况,因此仅需考虑前两种情况下的最大值即可。
综上所述,状态转移方程为:
- 当 s1[i - 1] == s2[j - 1] 时, dp[i][j] = dp[i - 1][j - 1] + s1[i] ;
- 当 s1[i - 1] != s2[j - 1] 时, dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
- 返回值:根据「状态表示」,我们不能直接返回 dp 表里面的某个值:
i. 先找到 dp[m][n] ,也是最大公共 ASCII 和;
ii. 统计两个字符串的 ASCII 码和 s u m;
iii. 返回 sum - 2 * dp[m][n]
代码如下:
class Solution {
public:
int minimumDeleteSum(string s1, string s2)
{
int m = s1.size(), n = s2.size();
//dp[i][j] 表⽰: s1 的 [0, i] 区间以及 s2 的 [0, j] 区间内的所有的⼦序列中,公共⼦序列的 ASCII 最⼤和。
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
s1 = ' ' + s1, s2 = ' ' + s2;
int sum = 0, flag = 1;
for(int i = 1; i <= m; i++)
{
for(int j = 1; j <= n; j++)
{
// 有s1[i]无s2[j] 或 无s1[i]有s2[j] (这两种情况包括无s1[i]无s2[j])
dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);
// 既有s1[i]也有s2[j]
if(s1[i] == s2[j]) dp[i][j] = max(dp[i][j], dp[i - 1][j - 1] + s1[i]);
if(flag) sum += s2[j]; // 计算 s2 字符串总和,不能在循环外计算,会把前面的 ' ' 加上
}
sum += s1[i]; // 计算 s1 字符串总和
flag = 0;
}
return sum - 2*dp[m][n];
}
};
8. 最长重复子数组
题目链接 -> Leetcode -718.最长重复子数组
Leetcode -718.最长重复子数组
题目:给两个整数数组 nums1 和 nums2 ,返回 两个数组中 公共的 、长度最长的子数组的长度 。
示例 1:
输入:nums1 = [1, 2, 3, 2, 1], nums2 = [3, 2, 1, 4, 7]
输出:3
解释:长度最长的公共子数组是[3, 2, 1] 。
示例 2:
输入:nums1 = [0, 0, 0, 0, 0], nums2 = [0, 0, 0, 0, 0]
输出:5
提示:
- 1 <= nums1.length, nums2.length <= 1000
- 0 <= nums1[i], nums2[i] <= 100
思路:子数组是数组中「连续」的一段,我们习惯上「以某一个位置为结尾」来研究。由于是两个数组,因此我们可以尝试:以第一个数组的 i 位置为结尾以及第二个数组的 j 位置为结尾来解决问题。
- 状态表示:dp[i][j] 表示「以第一个数组的 i 位置为结尾」,以及「第二个数组的 j 位置为结尾」公共的 、长度最长的「子数组」的长度。
- 状态转移方程:对于 dp[i][j] ,当 nums1[i] == nums2[j] 的时候,才有意义,此时最长重复子数组的长度应该等于 1 加上除去最后一个位置时,以 i - 1, j - 1 为结尾的最长重复子数组的长度。因此,状态转移方程为: dp[i][j] = 1 + dp[i - 1][j - 1]
- 返回值:根据「状态表示」,我们需要返回 dp 表里面的「最大值」
代码如下:
class Solution {
public:
int findLength(vector<int>& nums1, vector<int>& nums2)
{
int m = nums1.size(), n = nums2.size();
//dp[i][j] 表⽰「以第⼀个数组的 i 位置为结尾」,以及「第⼆个数组的 j 位置为结尾」公共的 、⻓度最⻓的「⼦数组」的⻓度
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
int ret = INT_MIN;
for(int i = 1; i <= m; i++)
{
for(int j = 1; j <= n; j++)
{
// 两个元素相等
if(nums1[i - 1] == nums2[j - 1]) dp[i][j] = max(dp[i][j], dp[i - 1][j - 1] + 1);
ret = max(ret, dp[i][j]);
}
}
return ret;
}
};